Oblicz Wysokość Trójkąta Równobocznego O Wymiarach Podanych Na Rysunku

Zmagasz się z geometrią i masz problem z obliczeniem wysokości trójkąta równobocznego? Nie martw się, wielu z nas tam było! Obliczenie wysokości trójkąta równobocznego, gdy masz podane jego wymiary, może wydawać się skomplikowane na pierwszy rzut oka, ale z odpowiednią wiedzą i kilkoma prostymi krokami, szybko opanujesz tę umiejętność. W tym artykule pokażę Ci, jak to zrobić krok po kroku, używając jasnych wyjaśnień i praktycznych przykładów.

Czym jest trójkąt równoboczny i dlaczego jego wysokość jest ważna?

Trójkąt równoboczny to trójkąt, w którym wszystkie trzy boki są równe, a co za tym idzie, wszystkie trzy kąty wewnętrzne mają miarę 60 stopni. Jego symetria sprawia, że obliczenia związane z nim są często prostsze niż w przypadku innych typów trójkątów.

Wysokość trójkąta równobocznego to odcinek prostej, który łączy wierzchołek z przeciwległym bokiem, tworząc z nim kąt prosty (90 stopni). Wysokość dzieli trójkąt równoboczny na dwa identyczne trójkąty prostokątne. Znajomość wysokości trójkąta jest kluczowa do obliczenia jego pola powierzchni, a także do rozwiązywania wielu problemów geometrycznych.

Metody obliczania wysokości trójkąta równobocznego

Istnieją zasadniczo dwie główne metody obliczania wysokości trójkąta równobocznego:

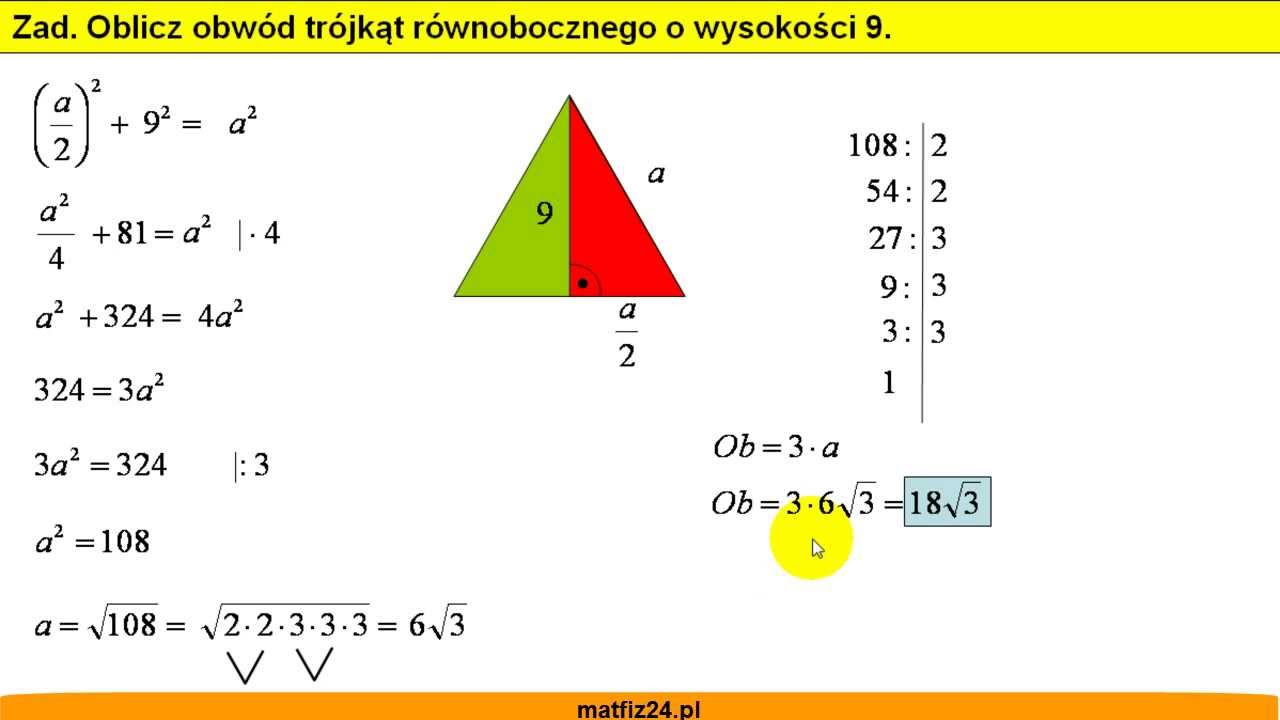
1. Użycie wzoru bezpośredniego

Najprostszym sposobem na obliczenie wysokości trójkąta równobocznego jest skorzystanie ze wzoru, który wyprowadzimy później przy użyciu twierdzenia Pitagorasa:

h = (a√3) / 2

Gdzie:

h to wysokość trójkąta
a to długość boku trójkąta

Przykład: Załóżmy, że trójkąt równoboczny ma bok o długości 6 cm. Aby obliczyć jego wysokość, podstawiamy wartość 'a' do wzoru:

h = (6√3) / 2 ≈ 5.196 cm

Zatem wysokość trójkąta równobocznego o boku 6 cm wynosi około 5.196 cm.

2. Użycie twierdzenia Pitagorasa

Jeśli wolisz rozumieć, skąd bierze się wzór, lub wolisz bazować na podstawowych zasadach geometrii, możesz użyć twierdzenia Pitagorasa. Pamiętaj, że wysokość dzieli trójkąt równoboczny na dwa identyczne trójkąty prostokątne. W każdym z tych trójkątów prostokątnych:

Przeciwprostokątna (najdłuższy bok) to bok trójkąta równobocznego ('a').
Jedna z przyprostokątnych to połowa boku trójkąta równobocznego (a/2).
Druga przyprostokątna to wysokość trójkąta równobocznego ('h').

Twierdzenie Pitagorasa mówi, że w trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej:

a² = b² + c²

W naszym przypadku:

a² = (a/2)² + h²

Teraz możemy przekształcić to równanie, aby wyznaczyć 'h':

h² = a² - (a/2)²

h² = a² - (a²/4)

h² = (3a²)/4

h = √(3a²/4)

h = (a√3) / 2

Jak widzisz, wyprowadziliśmy ten sam wzór, co w metodzie pierwszej!

Przykład: Użyjmy ponownie trójkąta równobocznego o boku 6 cm.

h² = 6² - (6/2)²

h² = 36 - 9

h² = 27

h = √27 ≈ 5.196 cm

Ponownie, otrzymujemy wysokość około 5.196 cm.

Kiedy używać której metody?

Wybór metody zależy od Twoich preferencji i od tego, co uważasz za prostsze. Jeśli zależy Ci na szybkości i masz dobrze zapamiętany wzór, metoda bezpośrednia będzie szybsza. Jeśli jednak lubisz rozumieć, skąd się biorą wzory, lub nie pamiętasz wzoru, twierdzenie Pitagorasa jest niezawodne.

Praktyczne zastosowania obliczania wysokości trójkąta równobocznego

Obliczanie wysokości trójkąta równobocznego znajduje zastosowanie w wielu dziedzinach, od geometrii i matematyki, po inżynierię, architekturę, a nawet sztukę. Oto kilka przykładów:

Obliczanie pola powierzchni: Jak wspomniano wcześniej, wysokość jest niezbędna do obliczenia pola powierzchni trójkąta równobocznego: Pole = (1/2) * podstawa * wysokość.
Konstrukcje geometryczne: Architekci i inżynierowie często wykorzystują trójkąty równoboczne w projektach budynków, mostów i innych konstrukcji. Znajomość wysokości jest kluczowa do zapewnienia stabilności i prawidłowego rozkładu obciążeń.
Projektowanie graficzne: Trójkąty równoboczne są często używane w projektowaniu logo, ikon i innych elementów graficznych.
Obliczanie objętości graniastosłupów i ostrosłupów: Wiedza o wysokości trójkąta równobocznego jest przydatna przy obliczaniu objętości figur przestrzennych, których podstawą jest trójkąt równoboczny.

Częste błędy i jak ich unikać

Podczas obliczania wysokości trójkąta równobocznego łatwo o kilka pomyłek. Oto najczęstsze z nich i jak ich unikać:

Pomylenie wzoru: Upewnij się, że używasz poprawnego wzoru: h = (a√3) / 2. Wielu początkujących myli go z innymi wzorami geometrycznymi.
Błędne podstawienie wartości: Sprawdź, czy prawidłowo podstawiasz długość boku ('a') do wzoru.
Błędy w obliczeniach: Zachowaj ostrożność podczas obliczeń, szczególnie przy operacjach na pierwiastkach kwadratowych. Użyj kalkulatora, aby uniknąć błędów.
Zapominanie o jednostkach: Pamiętaj o podawaniu jednostek (np. cm, m) przy podawaniu wyniku.

Podsumowanie i wnioski

Obliczenie wysokości trójkąta równobocznego jest proste, jeśli znasz odpowiednie wzory lub rozumiesz twierdzenie Pitagorasa. Wybierz metodę, która jest dla Ciebie najbardziej komfortowa i ćwicz, aby utrwalić wiedzę. Pamiętaj, że znajomość wysokości trójkąta równobocznego jest kluczowa w wielu dziedzinach, od matematyki po inżynierię i architekturę. Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, jak obliczyć wysokość trójkąta równobocznego i zainspirował Cię do dalszej nauki geometrii. Nie bój się pytać i eksperymentować! Powodzenia!

Pamiętaj, matematyka to nie tylko zbiór reguł, ale przede wszystkim logiczne myślenie i rozwiązywanie problemów. Każdy kolejny rozwiązany problem to krok naprzód w Twojej edukacji i rozwój Twoich umiejętności.