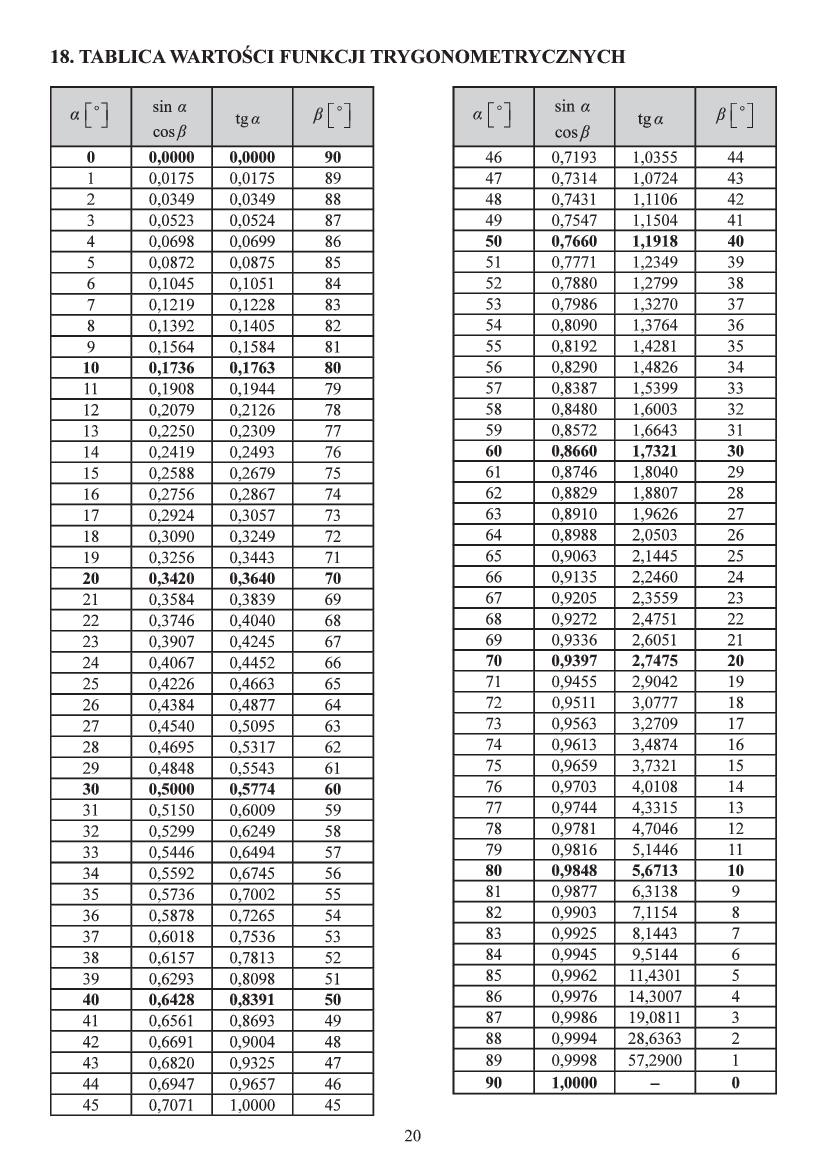
Oblicz Wartości Funkcji Trygonometrycznych Kątów Ostrych Trójkata Prostokątnego

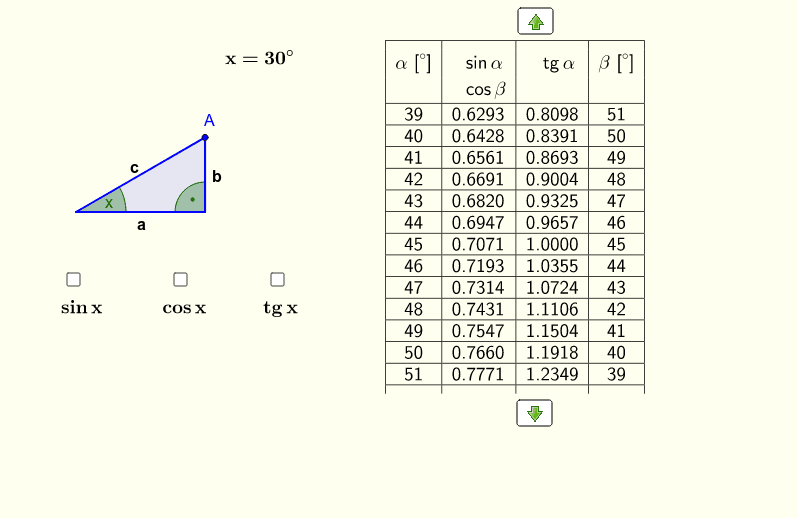
Dobrze, proszę bardzo. Opracowałem wyczerpujące wyjaśnienie obliczania wartości funkcji trygonometrycznych kątów ostrych w trójkącie prostokątnym.

Zacznijmy od podstaw. Mamy trójkąt prostokątny. Charakteryzuje się on jednym kątem prostym (90 stopni). Pozostałe dwa kąty są ostre (mniejsze niż 90 stopni). Funkcje trygonometryczne opisują relacje między długościami boków trójkąta a miarami tych kątów ostrych.

Podstawowe Funkcje Trygonometryczne

Mamy trzy podstawowe funkcje trygonometryczne: sinus (sin), cosinus (cos) i tangens (tan). Dla kąta ostrego α w trójkącie prostokątnym, definiujemy je następująco:

Sinus (sin α): Stosunek długości przyprostokątnej przeciwległej do kąta α do długości przeciwprostokątnej. Matematycznie: sin α = (długość przyprostokątnej przeciwległej) / (długość przeciwprostokątnej)
Cosinus (cos α): Stosunek długości przyprostokątnej przyległej do kąta α do długości przeciwprostokątnej. Matematycznie: cos α = (długość przyprostokątnej przyległej) / (długość przeciwprostokątnej)
Tangens (tan α): Stosunek długości przyprostokątnej przeciwległej do kąta α do długości przyprostokątnej przyległej do kąta α. Matematycznie: tan α = (długość przyprostokątnej przeciwległej) / (długość przyprostokątnej przyległej)

Przeciwprostokątna, Przyprostokątna Przeciwległa i Przyległa

Zidentyfikowanie boków jest kluczowe:

Przeciwprostokątna: Zawsze najdłuższy bok trójkąta prostokątnego. Leży naprzeciwko kąta prostego. Jest unikalna.
Przyprostokątna Przeciwległa: Leży naprzeciwko rozważanego kąta ostrego (α). Jej identyfikacja zależy od tego, który kąt α rozważamy.
Przyprostokątna Przyległa: Leży obok rozważanego kąta ostrego (α) i nie jest przeciwprostokątną. Jej identyfikacja, podobnie jak przyprostokątnej przeciwległej, zależy od rozważanego kąta α.

Obliczanie Wartości Funkcji Trygonometrycznych

Zidentyfikuj Trójkąt Prostokątny: Upewnij się, że masz do czynienia z trójkątem prostokątnym. Jest to fundamentalne wymaganie.
Określ Długości Boków: Zmierz lub odczytaj z rysunku (lub danych zadania) długości wszystkich trzech boków trójkąta: przeciwprostokątnej, przyprostokątnej przeciwległej i przyprostokątnej przyległej względem kąta, dla którego chcesz obliczyć wartości funkcji trygonometrycznych.
Wybierz Kąt: Zdecyduj, dla którego kąta ostrego (α) chcesz obliczyć wartości funkcji. Pamiętaj, że przyprostokątna przeciwległa i przyległa zmieniają się w zależności od tego, który kąt wybierzesz.
Zastosuj Definicje: Użyj podanych wyżej definicji sinusa, cosinusa i tangensa, podstawiając odpowiednie wartości długości boków do wzorów.
Oblicz: Wykonaj dzielenie, aby otrzymać wartości funkcji trygonometrycznych. Wyniki będą liczbami rzeczywistymi (zazwyczaj ułamkami lub liczbami dziesiętnymi).

Funkcje Trygonometryczne Kątów Uzupełniających

W trójkącie prostokątnym, kąty ostre są kątami uzupełniającymi się, co oznacza, że ich suma wynosi 90 stopni. Jeśli jeden kąt ostry oznaczmy jako α, to drugi kąt ostry będzie miał miarę 90° - α. Istnieje interesująca zależność między funkcjami trygonometrycznymi kątów uzupełniających się:

sin α = cos (90° - α)
cos α = sin (90° - α)
tan α = 1 / tan (90° - α) (czyli tangens jednego kąta jest odwrotnością tangensa drugiego kąta)

Funkcje Kotangens, Sekans i Kosekans

Oprócz sinusa, cosinusa i tangensa, istnieją również trzy inne funkcje trygonometryczne, które są zdefiniowane jako odwrotności tych pierwszych trzech:

Kotangens (cot α): Odwrotność tangensa. cot α = 1 / tan α = (długość przyprostokątnej przyległej) / (długość przyprostokątnej przeciwległej)
Sekans (sec α): Odwrotność cosinusa. sec α = 1 / cos α = (długość przeciwprostokątnej) / (długość przyprostokątnej przyległej)
Kosekans (csc α): Odwrotność sinusa. csc α = 1 / sin α = (długość przeciwprostokątnej) / (długość przyprostokątnej przeciwległej)

Zauważ, że znając wartości sinusa, cosinusa i tangensa dla danego kąta, bardzo łatwo obliczyć wartości kotangensa, sekansa i kosekansa – wystarczy obliczyć odwrotności.

Przykłady

Załóżmy, że mamy trójkąt prostokątny, w którym:

Długość przyprostokątnej przeciwległej do kąta α wynosi 3.
Długość przyprostokątnej przyległej do kąta α wynosi 4.
Długość przeciwprostokątnej wynosi 5 (sprawdź twierdzenie Pitagorasa: 3² + 4² = 5²).

Wtedy:

sin α = 3 / 5 = 0.6
cos α = 4 / 5 = 0.8
tan α = 3 / 4 = 0.75
cot α = 4 / 3 = 1.333...
sec α = 5 / 4 = 1.25
csc α = 5 / 3 = 1.666...

Teraz, rozważmy drugi kąt ostry, β, w tym samym trójkącie. Wtedy przyprostokątna przeciwległa do kąta β ma długość 4, a przyprostokątna przyległa ma długość 3. Przeciwprostokątna pozostaje taka sama (długość 5).

sin β = 4 / 5 = 0.8 (zauważ, że sin β = cos α)
cos β = 3 / 5 = 0.6 (zauważ, że cos β = sin α)
tan β = 4 / 3 = 1.333... (zauważ, że tan β = 1 / tan α)
cot β = 3 / 4 = 0.75
sec β = 5 / 3 = 1.666...
csc β = 5 / 4 = 1.25

Wartości Funkcji Trygonometrycznych Dla Kątów Specjalnych

Niektóre kąty ostre pojawiają się często w problemach trygonometrycznych. Warto znać wartości funkcji trygonometrycznych dla tych kątów: 30°, 45° i 60°. Można je wyprowadzić geometrycznie, analizując specjalne trójkąty: trójkąt równoboczny podzielony na dwa trójkąty prostokątne o kątach 30° i 60° oraz trójkąt prostokątny równoramienny o kątach 45°.

30 stopni (π/6 radiana):
- sin 30° = 1/2
- cos 30° = √3/2
- tan 30° = √3/3
45 stopni (π/4 radiana):
- sin 45° = √2/2
- cos 45° = √2/2
- tan 45° = 1
60 stopni (π/3 radiana):
- sin 60° = √3/2
- cos 60° = 1/2
- tan 60° = √3

Zastosowania

Funkcje trygonometryczne mają szerokie zastosowanie w wielu dziedzinach nauki i inżynierii, w tym:

Nawigacja: Określanie pozycji i kierunku.
Fizyka: Analiza ruchu, fal i drgań.
Inżynieria: Projektowanie mostów, budynków i innych konstrukcji.
Astronomia: Obliczanie odległości do gwiazd i planet.
Geodezja: Pomiary terenowe i tworzenie map.

Pamiętaj, że precyzja obliczeń zależy od dokładności pomiarów długości boków trójkąta. Ponadto, kalkulatory i programy komputerowe posiadają wbudowane funkcje trygonometryczne, które pozwalają na szybkie i dokładne obliczenia, zwłaszcza dla kątów innych niż te specjalne. Ważne jest jednak, aby rozumieć podstawy teoretyczne, aby móc prawidłowo interpretować wyniki i rozwiązywać problemy.