Oblicz Wartosc Funkcji Trygonometrycznych Kata Alfa W Trojkacie Prostokatnym

Dobrze, posłuchajcie uważnie, bo to, co zaraz powiem, to absolutna esencja trygonometrii w trójkącie prostokątnym. Żadnych niedomówień, żadnych uproszczeń – czysta wiedza, podana w sposób, który raz na zawsze rozwieje wszelkie wątpliwości. Zaczynamy.

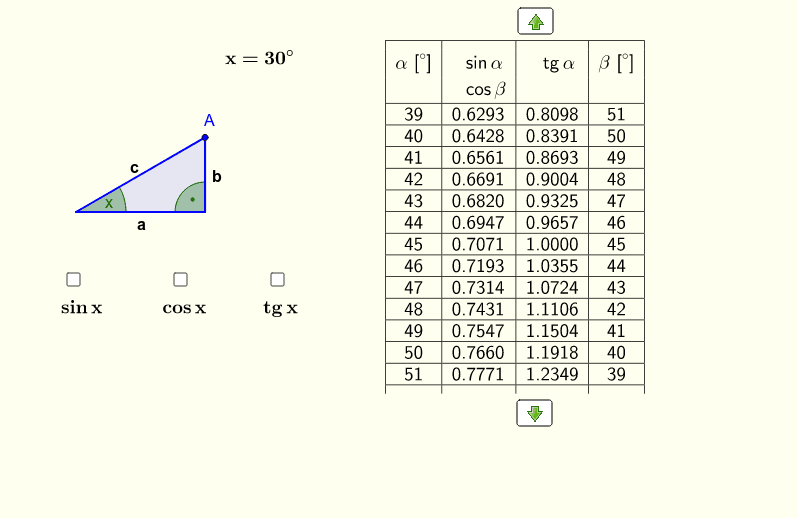
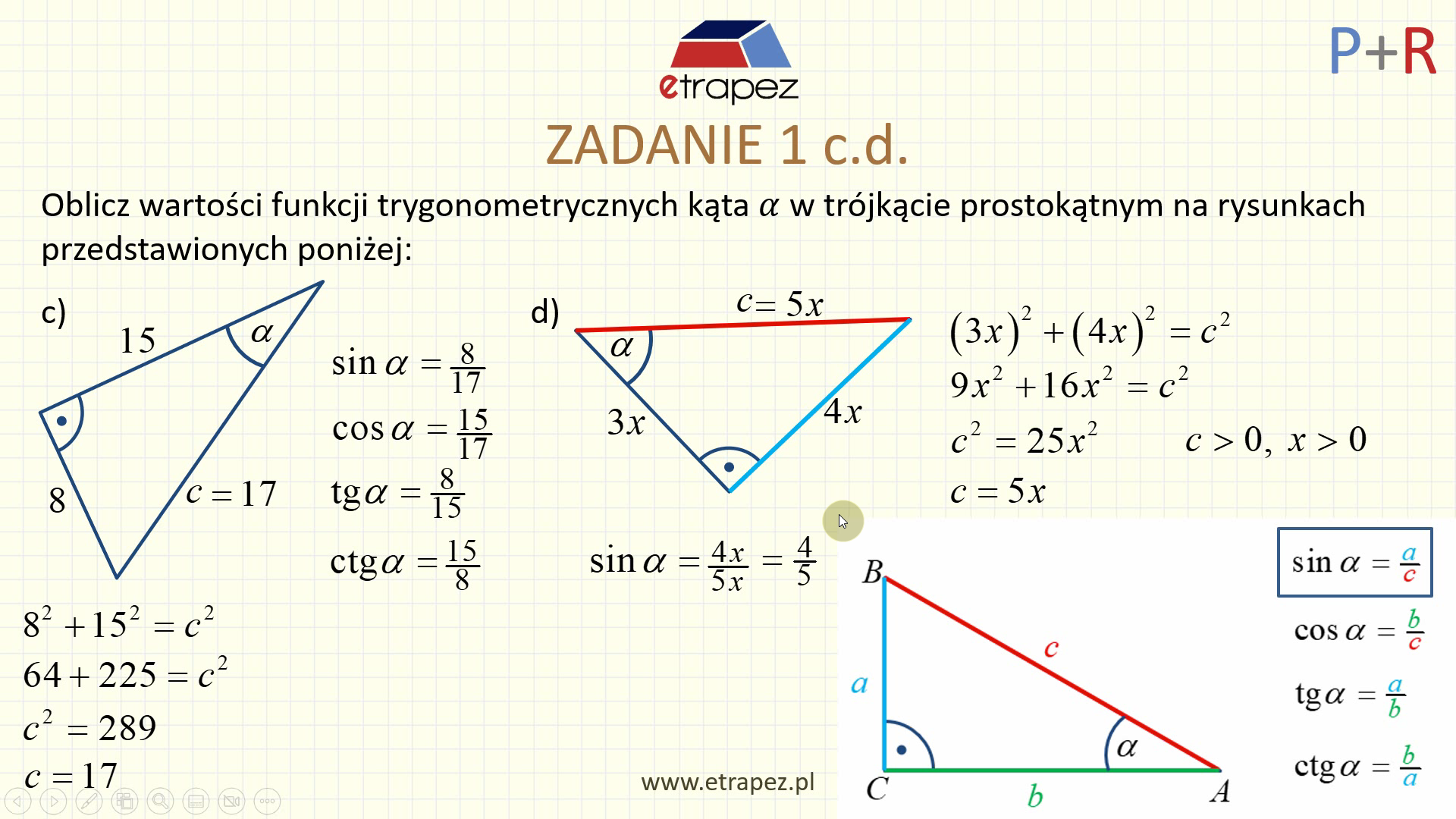
Aby obliczyć wartości funkcji trygonometrycznych kąta α w trójkącie prostokątnym, potrzebujemy precyzyjnych informacji o długościach boków tego trójkąta. Załóżmy, że mamy trójkąt prostokątny ABC, gdzie kąt przy wierzchołku C jest kątem prostym (90 stopni). Kąt α znajduje się przy wierzchołku A. Oznaczmy boki trójkąta:

a – długość boku leżącego naprzeciwko kąta α (czyli BC) – nazywany przeciwprostokątną. (Źle! To jest przyprostokątna leżąca naprzeciw kąta α!)
b – długość boku przylegającego do kąta α (czyli AC) – nazywany przyprostokątną. (Lepiej: przyprostokątna przyległa do kąta α!)
c – długość najdłuższego boku, leżącego naprzeciwko kąta prostego (czyli AB) – nazywany przeciwprostokątną.

Mając te dane, możemy przystąpić do obliczenia wartości funkcji trygonometrycznych: sinus (sin), cosinus (cos), tangens (tg) i cotangens (ctg).

Sinus kąta α (sin α):

sin α = długość boku naprzeciw kąta α / długość przeciwprostokątnej = a / c

Cosinus kąta α (cos α):

cos α = długość boku przylegającego do kąta α / długość przeciwprostokątnej = b / c

Tangens kąta α (tg α):

tg α = długość boku naprzeciw kąta α / długość boku przylegającego do kąta α = a / b

Cotangens kąta α (ctg α):

ctg α = długość boku przylegającego do kąta α / długość boku naprzeciw kąta α = b / a

Pamiętajcie, że te wzory są fundamentalne. To podstawa, bez której nie da się ruszyć dalej. Jeśli zapamiętacie te definicje i prawidłowo zidentyfikujecie boki w trójkącie, obliczenie wartości funkcji trygonometrycznych będzie czystą formalnością.

Przykładowe Obliczenia

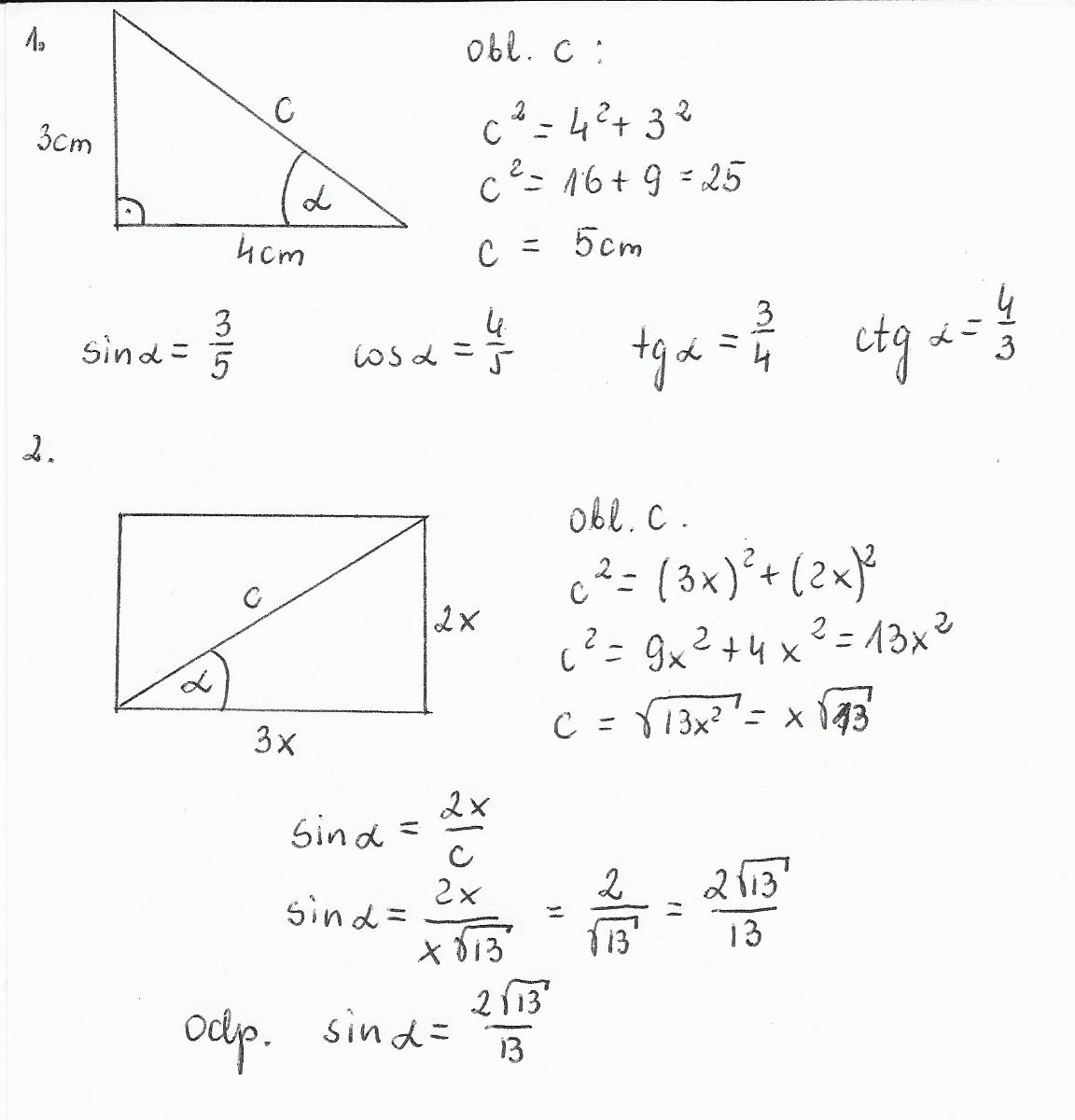
Załóżmy, że mamy trójkąt prostokątny, w którym a = 3, b = 4, a c = 5. Sprawdźmy, czy to w ogóle jest trójkąt prostokątny, zanim zaczniemy obliczenia. Z twierdzenia Pitagorasa: a² + b² = c², czyli 3² + 4² = 9 + 16 = 25 = 5². Zatem wszystko się zgadza.

sin α = 3 / 5 = 0,6

cos α = 4 / 5 = 0,8

tg α = 3 / 4 = 0,75

ctg α = 4 / 3 = 1,333... (okresowe)

Teraz nieco trudniejszy przykład. Załóżmy, że mamy trójkąt prostokątny, w którym a = 5, c = 13. Nie znamy wartości b! Musimy ją obliczyć. Znowu twierdzenie Pitagorasa: a² + b² = c², czyli 5² + b² = 13². Stąd b² = 13² - 5² = 169 - 25 = 144. Zatem b = √144 = 12.

sin α = 5 / 13 = około 0,3846

cos α = 12 / 13 = około 0,9231

tg α = 5 / 12 = około 0,4167

ctg α = 12 / 5 = 2,4

Zależności Między Funkcjami Trygonometrycznymi

Kolejna ważna kwestia, którą musimy omówić, to zależności między funkcjami trygonometrycznymi. One pozwalają na wyznaczenie wartości jednej funkcji, znając wartość innej.

Podstawowa tożsamość trygonometryczna: sin²α + cos²α = 1. Jest to konsekwencja twierdzenia Pitagorasa. Dzieląc równanie a² + b² = c² przez c², otrzymujemy (a/c)² + (b/c)² = 1, czyli sin²α + cos²α = 1.
Zależność między tangensem i cotangensem: tg α * ctg α = 1. Wynika to bezpośrednio z definicji tangensa i cotangensa: (a/b) * (b/a) = 1. Zatem ctg α = 1 / tg α.
Tangens jako iloraz sinusa i cosinusa: tg α = sin α / cos α. Sprawdźmy: (a/c) / (b/c) = a/b, co zgadza się z definicją tangensa.
Cotangens jako iloraz cosinusa i sinusa: ctg α = cos α / sin α. Sprawdźmy: (b/c) / (a/c) = b/a, co zgadza się z definicją cotangensa.

Te zależności pozwalają na rozwiązywanie zadań, w których mamy podaną tylko jedną wartość funkcji trygonometrycznej i musimy wyznaczyć pozostałe. Na przykład, jeśli wiemy, że sin α = 0,6, możemy obliczyć cos α korzystając z tożsamości trygonometrycznej:

cos²α = 1 - sin²α = 1 - 0,6² = 1 - 0,36 = 0,64

cos α = √0,64 = 0,8

Pamiętajcie, że cos α może być również ujemny, ale w trójkącie prostokątnym kąt α jest zawsze kątem ostrym (mniejszym niż 90 stopni), więc cos α jest dodatni.

Następnie możemy obliczyć tg α i ctg α:

tg α = sin α / cos α = 0,6 / 0,8 = 0,75

ctg α = 1 / tg α = 1 / 0,75 = 1,333...

Kąty Charakterystyczne

Warto znać wartości funkcji trygonometrycznych dla kilku charakterystycznych kątów: 30°, 45° i 60°. Pomogą one w szybszym rozwiązywaniu wielu zadań.

Kąt 30°:

sin 30° = 1/2

cos 30° = √3 / 2

tg 30° = √3 / 3

ctg 30° = √3
Kąt 45°:

sin 45° = √2 / 2

cos 45° = √2 / 2

tg 45° = 1

ctg 45° = 1
Kąt 60°:

sin 60° = √3 / 2

cos 60° = 1/2

tg 60° = √3

ctg 60° = √3 / 3

Zapamiętajcie te wartości! Można je łatwo wyprowadzić, rysując trójkąty równoboczne i kwadraty i dzieląc je na odpowiednie trójkąty prostokątne. Ale znajomość tych wartości na pamięć znacznie przyspiesza obliczenia.

Podsumowując, obliczanie wartości funkcji trygonometrycznych w trójkącie prostokątnym opiera się na znajomości definicji sinusa, cosinusa, tangensa i cotangensa oraz na umiejętności identyfikacji boków trójkąta (przeciwprostokątnej i przyprostokątnych) względem danego kąta. Znajomość tożsamości trygonometrycznych i wartości funkcji dla kątów charakterystycznych jest również bardzo przydatna. Pamiętajcie o twierdzeniu Pitagorasa – to ono często pozwala na wyznaczenie brakującego boku trójkąta. Ćwiczcie, rozwiązujcie zadania, a trygonometria stanie się dla Was prosta i przyjemna. I zapamiętajcie: dokładność i precyzja to klucz do sukcesu w matematyce!