Oblicz Pole Rombu Którego Bok Ma Długość 6

Czy kiedykolwiek zastanawiałeś się, jak obliczyć pole rombu? Wydaje się to skomplikowane, ale tak naprawdę, znając odpowiednie wzory i mając podstawowe dane, staje się to zadaniem dostępnym dla każdego. Ten artykuł jest skierowany do uczniów, studentów, a także wszystkich osób, które chcą odświeżyć swoją wiedzę z geometrii lub po prostu dowiedzieć się czegoś nowego. Skupimy się na przypadku rombu, którego bok ma długość 6 jednostek, pokazując krok po kroku, jak obliczyć jego pole.

Zacznijmy od podstaw – czym w ogóle jest romb?

Co to jest Romb?

Romb to specjalny rodzaj równoległoboku. Charakteryzuje się tym, że wszystkie jego boki są równej długości. Oprócz tego:

Przeciwległe kąty rombu są równe.
Przekątne rombu przecinają się w połowie pod kątem prostym.
Przekątne rombu dzielą go na cztery przystające trójkąty prostokątne.

Te właściwości są kluczowe do zrozumienia, jak obliczyć pole rombu.

Metody Obliczania Pola Rombu

Istnieje kilka metod obliczania pola rombu. Przyjrzyjmy się im bliżej, a następnie skupimy się na przypadkach, gdy znamy długość boku (w naszym przypadku 6 jednostek).

1. Pole rombu z wykorzystaniem przekątnych

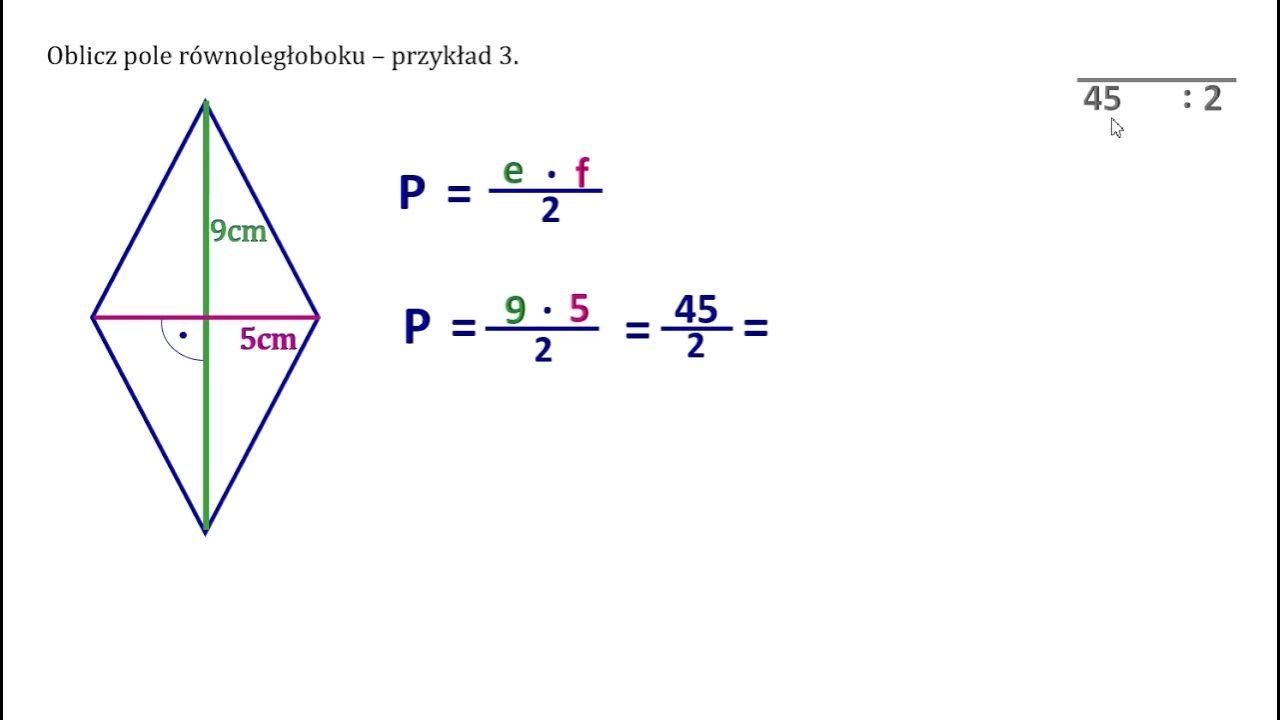
Najpopularniejszy wzór na pole rombu wykorzystuje długości jego przekątnych. Oznaczmy długości przekątnych jako d₁ i d₂. Wówczas pole rombu (P) obliczamy w następujący sposób:

P = (d₁ * d₂) / 2

Oznacza to, że pole rombu jest równe połowie iloczynu jego przekątnych.

2. Pole rombu z wykorzystaniem boku i wysokości

Podobnie jak w przypadku równoległoboku, pole rombu można obliczyć, mnożąc długość boku przez wysokość opuszczoną na ten bok. Oznaczmy długość boku jako a, a wysokość jako h. Wtedy:

P = a * h

W naszym przypadku, gdzie bok a ma długość 6, wzór upraszcza się do:

P = 6 * h

3. Pole rombu z wykorzystaniem boku i kąta

Jeśli znamy długość boku a i miarę jednego z kątów rombu (oznaczmy go jako α), to pole rombu można obliczyć za pomocą wzoru:

P = a² * sin(α)

W naszym przypadku, gdzie a = 6, wzór przyjmuje postać:

P = 36 * sin(α)

Obliczanie Pola Rombu o Boku Długości 6 - Praktyczne Przykłady

Teraz, gdy znamy różne wzory, przyjrzyjmy się, jak możemy obliczyć pole rombu, wiedząc, że długość jego boku wynosi 6 jednostek. Kluczowe jest, aby dysponować dodatkowymi informacjami – albo długością jednej z przekątnych, albo wysokością, albo miarą jednego z kątów.

Przykład 1: Znamy Długość Jednej z Przekątnych

Załóżmy, że jedna z przekątnych naszego rombu ma długość 8. Niech będzie to d₁ = 8. Aby obliczyć pole, potrzebujemy długości drugiej przekątnej (d₂).

Wykorzystamy fakt, że przekątne rombu przecinają się w połowie pod kątem prostym. Oznacza to, że połowa przekątnej d₁ (czyli 4) oraz połowa przekątnej d₂ tworzą przyprostokątne trójkąta prostokątnego, którego przeciwprostokątną jest bok rombu (długości 6). Możemy użyć twierdzenia Pitagorasa:

(d₁/2)² + (d₂/2)² = a²

Podstawiając nasze dane:

4² + (d₂/2)² = 6²

16 + (d₂/2)² = 36

(d₂/2)² = 20

d₂/2 = √20 = 2√5

d₂ = 4√5

Teraz możemy obliczyć pole:

P = (d₁ * d₂) / 2 = (8 * 4√5) / 2 = 16√5

Zatem pole rombu wynosi 16√5 jednostek kwadratowych.

Przykład 2: Znamy Wysokość Rombu

Załóżmy, że wysokość rombu (h) wynosi 4. Wtedy, korzystając ze wzoru P = a * h:

P = 6 * 4 = 24

Pole rombu wynosi 24 jednostki kwadratowe.

Przykład 3: Znamy Kąt Rombu

Załóżmy, że jeden z kątów rombu wynosi 60 stopni (α = 60°). Wtedy:

P = a² * sin(α) = 6² * sin(60°) = 36 * (√3 / 2) = 18√3

Pole rombu wynosi 18√3 jednostek kwadratowych.

Dlaczego To Jest Ważne?

Zrozumienie, jak obliczyć pole rombu, nie tylko pomaga w rozwiązywaniu zadań z matematyki. Geometria otacza nas na co dzień. Architektura, design, a nawet sztuka często wykorzystują figury geometryczne, w tym romby. Umiejętność obliczania pola rombu może być przydatna w różnych sytuacjach praktycznych, np. przy projektowaniu wzorów na podłogę, obliczaniu powierzchni dachu w kształcie rombu, czy też przy tworzeniu grafik.

Podsumowanie i Wskazówki

Pamiętaj, że romb to równoległobok o wszystkich bokach równej długości.
Istnieją różne wzory na pole rombu – wybierz ten, który pasuje do dostępnych danych.
Zwróć uwagę na jednostki – pole zawsze wyrażamy w jednostkach kwadratowych.
Jeśli masz podane tylko długość boku, poszukaj dodatkowych informacji – długości przekątnych, wysokości lub kąta.
Wykorzystuj twierdzenie Pitagorasa do znalezienia brakujących danych, jeśli znasz długość boku i jednej z przekątnych.

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, jak obliczyć pole rombu, którego bok ma długość 6. Pamiętaj, praktyka czyni mistrza! Rozwiązuj zadania, analizuj przykłady, a z pewnością opanujesz tę umiejętność. Powodzenia!