Oblicz Pole Powierzchni Całkowitej Ostrosłupa Prawidłowego Trójkatnego

Dobrze, przygotujmy się do zgłębienia tematu pola powierzchni całkowitej ostrosłupa prawidłowego trójkątnego. Rozważmy, że dysponujemy tutaj kompletnym kompendium wiedzy na ten temat.

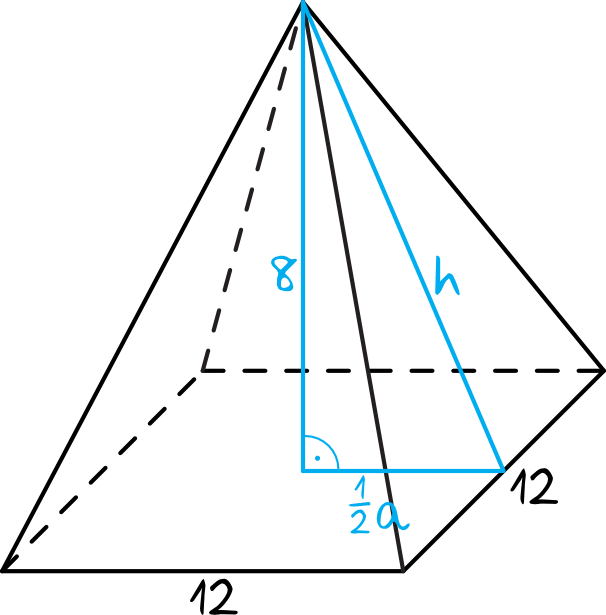
Zacznijmy od definicji. Ostrosłup prawidłowy trójkątny to bryła, której podstawą jest trójkąt równoboczny, a wszystkie ściany boczne są trójkątami równoramiennymi, nachylonymi do podstawy pod tym samym kątem. Kluczowe jest słowo "prawidłowy", ponieważ gwarantuje ono regularność i symetrię, co znacznie upraszcza obliczenia. Pole powierzchni całkowitej takiego ostrosłupa to, najprościej mówiąc, suma pól wszystkich jego ścian: jednej podstawy (trójkąta równobocznego) i trzech identycznych ścian bocznych (trójkątów równoramiennych).

Aby obliczyć pole powierzchni całkowitej ostrosłupa prawidłowego trójkątnego, potrzebujemy kilku informacji. Najważniejsze są:

• a – długość krawędzi podstawy (boku trójkąta równobocznego w podstawie)
• h – wysokość ściany bocznej (wysokość trójkąta równoramiennego stanowiącego ścianę boczną, opuszczona na krawędź podstawy)

Jeżeli nie znamy bezpośrednio wysokości ściany bocznej (h), ale znamy inne dane, takie jak wysokość ostrosłupa (H) i np. odległość spodka wysokości ostrosłupa od krawędzi podstawy (r), to możemy ją obliczyć, korzystając z twierdzenia Pitagorasa. O tym jednak za chwilę.

Obliczanie Pola Podstawy

Podstawą naszego ostrosłupa jest trójkąt równoboczny. Wzór na pole trójkąta równobocznego o boku a jest powszechnie znany i wynosi:

Pp = (a²√3) / 4

To fundamentalna zależność, którą musimy zapamiętać. Nie ma tu żadnych skrótów ani uproszczeń – to jest wzór, którego używamy zawsze, gdy mamy do czynienia z trójkątem równobocznym.

Obliczanie Pola Powierzchni Bocznej

Pole powierzchni bocznej (Pb) to suma pól trzech identycznych trójkątów równoramiennych, które stanowią ściany boczne. Pole jednego takiego trójkąta to połowa iloczynu długości jego podstawy (czyli krawędzi podstawy ostrosłupa, a) i wysokości opuszczonej na tę podstawę (czyli wysokości ściany bocznej, h):

Pole jednego trójkąta = (a * h) / 2

Ponieważ mamy trzy takie trójkąty, pole powierzchni bocznej wynosi:

Pb = 3 * (a * h) / 2 = (3ah) / 2

To również prosta i kluczowa zależność. Musimy mieć pewność, że dobrze identyfikujemy wysokość ściany bocznej (h) – to nie jest wysokość ostrosłupa! To wysokość trójkąta równoramiennego, który tworzy ścianę boczną.

Obliczanie Pola Powierzchni Całkowitej

Teraz, gdy mamy już policzone pole podstawy (Pp) i pole powierzchni bocznej (Pb), możemy obliczyć pole powierzchni całkowitej (Pc) ostrosłupa. To po prostu suma tych dwóch pól:

Pc = Pp + Pb = (a²√3) / 4 + (3ah) / 2

To jest wzór, którego szukaliśmy. Wystarczy podstawić do niego znane wartości a i h, aby uzyskać pole powierzchni całkowitej ostrosłupa prawidłowego trójkątnego.

Sytuacje, w których nie znamy bezpośrednio h

Załóżmy, że nie znamy bezpośrednio wysokości ściany bocznej (h), ale znamy wysokość ostrosłupa (H) i długość krawędzi podstawy (a). W takiej sytuacji musimy posłużyć się twierdzeniem Pitagorasa, aby wyznaczyć h.

Wyobraźmy sobie trójkąt prostokątny, którego przyprostokątnymi są wysokość ostrosłupa (H) i odległość spodka wysokości ostrosłupa od krawędzi podstawy (r), a przeciwprostokątną jest właśnie wysokość ściany bocznej (h). Odległość r to promień okręgu wpisanego w trójkąt równoboczny o boku a. Wzór na promień okręgu wpisanego w trójkąt równoboczny to:

r = (a√3) / 6

Teraz możemy zastosować twierdzenie Pitagorasa:

H² + r² = h²

Czyli:

h² = H² + ((a√3) / 6)² = H² + (3a²) / 36 = H² + a²/12

Stąd:

h = √(H² + a²/12)

Mając obliczone h, możemy wrócić do wzoru na pole powierzchni całkowitej i dokończyć obliczenia.

Przykład liczbowy

Załóżmy, że krawędź podstawy ostrosłupa prawidłowego trójkątnego wynosi a = 6 cm, a wysokość ściany bocznej wynosi h = 5 cm. Obliczmy pole powierzchni całkowitej.

Pp = (a²√3) / 4 = (6²√3) / 4 = (36√3) / 4 = 9√3 cm²

Pb = (3ah) / 2 = (3 * 6 * 5) / 2 = 90 / 2 = 45 cm²

Pc = Pp + Pb = 9√3 + 45 cm²

Możemy przybliżyć wartość √3 jako 1.73, wtedy:

Pc ≈ 9 * 1.73 + 45 ≈ 15.57 + 45 ≈ 60.57 cm²

Zatem pole powierzchni całkowitej tego ostrosłupa wynosi około 60.57 cm².

Inne możliwości

Możemy napotkać sytuacje, w których zamiast wysokości ściany bocznej (h) podany jest kąt nachylenia ściany bocznej do płaszczyzny podstawy (α). W takim przypadku, możemy wykorzystać funkcje trygonometryczne, aby powiązać h, H i r.

Wspomnieliśmy już, że r = (a√3) / 6. Tangens kąta α w trójkącie prostokątnym utworzonym przez wysokość ostrosłupa (H), odległość r i wysokość ściany bocznej (h) wyraża się następująco:

tan(α) = H / r = H / ((a√3) / 6) = (6H) / (a√3)

Zatem, jeśli znamy kąt α i krawędź podstawy a, możemy obliczyć wysokość ostrosłupa H:

H = (a√3 * tan(α)) / 6

Następnie, korzystając z twierdzenia Pitagorasa, możemy obliczyć wysokość ściany bocznej h:

h = √(H² + r²) = √(((a√3 * tan(α)) / 6)² + ((a√3) / 6)²)

I ostatecznie, mając h, możemy obliczyć pole powierzchni całkowitej jak wcześniej.

Podsumowując, kluczowe w obliczaniu pola powierzchni całkowitej ostrosłupa prawidłowego trójkątnego jest zrozumienie geometrii bryły, poprawne identyfikowanie danych i umiejętne stosowanie wzorów na pole trójkąta równobocznego, pole trójkąta i twierdzenia Pitagorasa. Różne warianty zadania wymagają elastyczności i umiejętności przekształcania wzorów, ale zasada pozostaje ta sama: suma pól wszystkich ścian.