Oblicz Pole Każdego Z Poniższych Rombów

Czy kiedykolwiek patrzyłeś na diamentowy wzór i zastanawiałeś się, jak obliczyć jego powierzchnię? A może po prostu potrzebujesz odświeżyć swoją wiedzę z geometrii? Jeśli tak, to jesteś we właściwym miejscu! Ten artykuł jest stworzony dla uczniów, studentów, a także dla każdego, kto chce przypomnieć sobie, jak efektywnie obliczać pole powierzchni rombu. Razem zgłębimy tajniki tego fascynującego kształtu geometrycznego, korzystając z różnych metod i wzorów. Przygotuj się na podróż pełną praktycznych przykładów i klarownych wyjaśnień. Zaczynamy!

Co to jest Romb?

Zanim przejdziemy do obliczeń, upewnijmy się, że wszyscy rozumiemy, czym tak naprawdę jest romb. Romb to czworokąt, który charakteryzuje się następującymi cechami:

• Wszystkie cztery boki mają równą długość.
• Przeciwległe kąty są równe.
• Przekątne przecinają się pod kątem prostym i dzielą się na połowy.

Romb jest szczególnym przypadkiem równoległoboku, w którym wszystkie boki są tej samej długości. Kwadrat jest szczególnym przypadkiem rombu, w którym wszystkie kąty są proste.

Metody Obliczania Pola Rombu

Istnieje kilka sposobów na obliczenie pola powierzchni rombu. Wybór metody zależy od tego, jakie dane są nam dostępne. Przyjrzyjmy się najpopularniejszym z nich:

1. Pole rombu na podstawie długości przekątnych

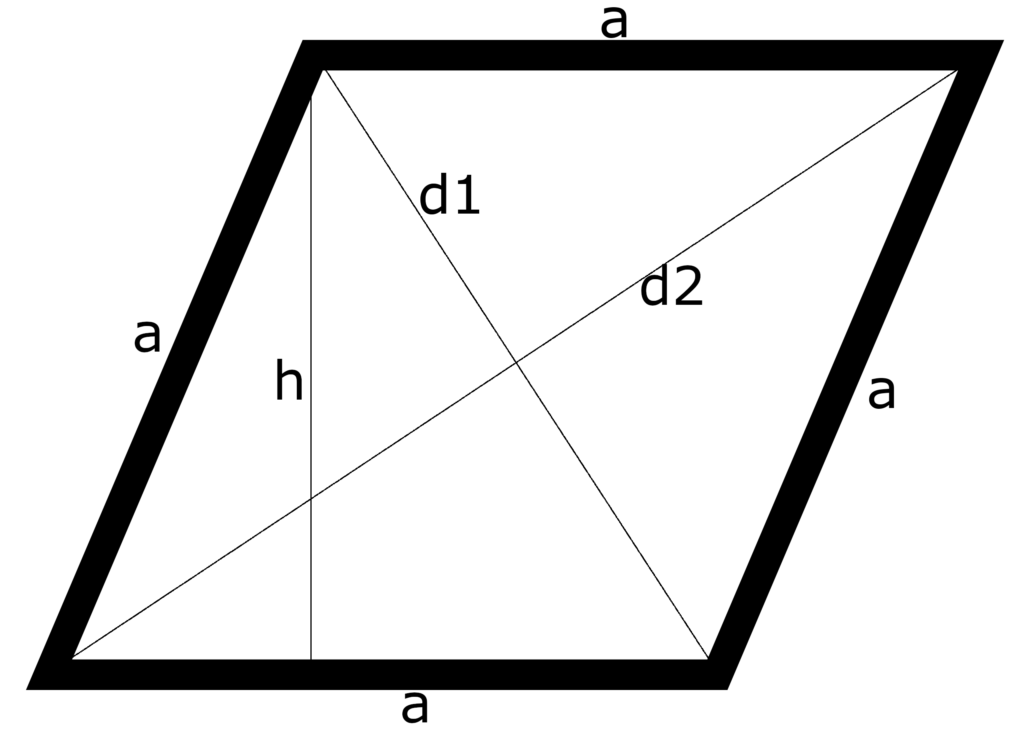
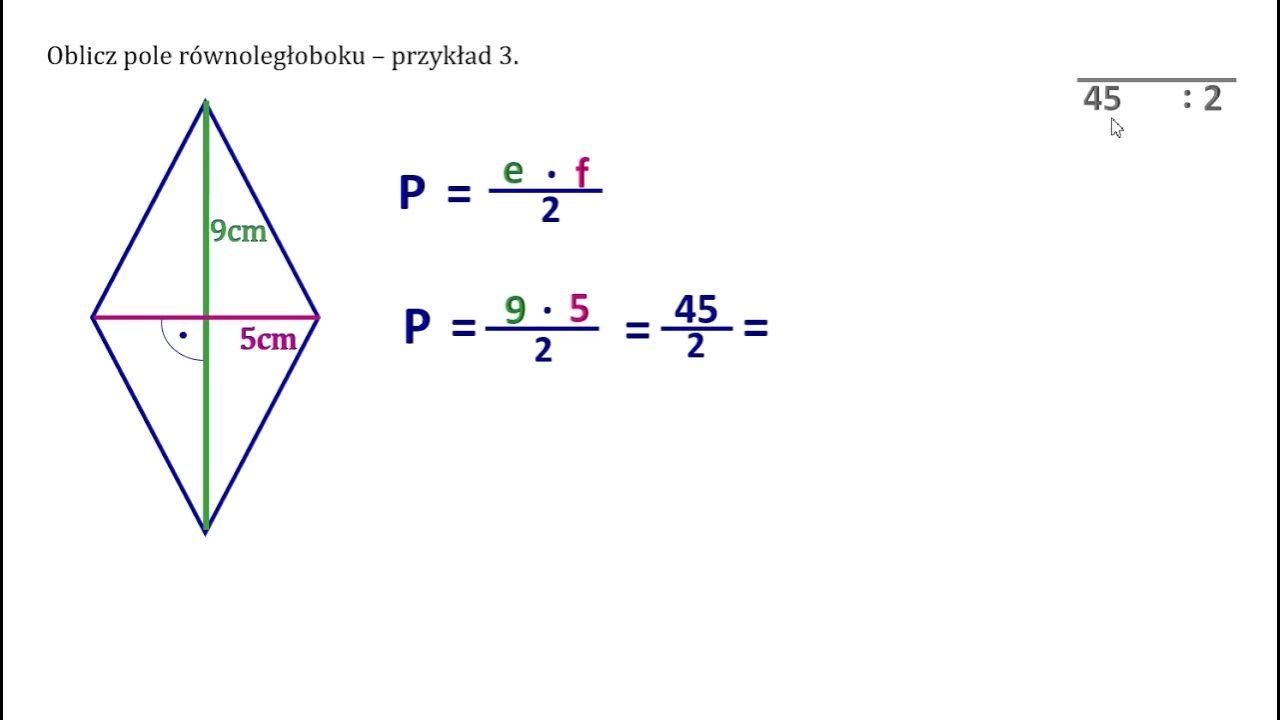
To najczęściej stosowana i najprostsza metoda. Potrzebujemy znać długości obu przekątnych rombu. Oznaczmy je jako d₁ i d₂. Wówczas pole rombu (P) możemy obliczyć za pomocą wzoru:

P = (d₁ * d₂) / 2

Przykład: Załóżmy, że romb ma przekątne o długościach 6 cm i 8 cm. Wtedy jego pole wynosi:

P = (6 cm * 8 cm) / 2 = 24 cm²

2. Pole rombu na podstawie długości boku i wysokości

Jeśli znamy długość boku rombu (a) oraz wysokość opuszczoną na ten bok (h), możemy obliczyć pole rombu, korzystając ze wzoru:

P = a * h

Wysokość rombu to odległość między dwoma równoległymi bokami.

Przykład: Romb ma bok długości 5 cm, a jego wysokość wynosi 4 cm. Wtedy jego pole wynosi:

P = 5 cm * 4 cm = 20 cm²

3. Pole rombu na podstawie długości boku i kąta

Jeżeli znamy długość boku rombu (a) oraz miarę jednego z kątów wewnętrznych (α), możemy obliczyć pole rombu, wykorzystując funkcję sinus. Wzór wygląda następująco:

P = a² * sin(α)

Pamiętaj, że α to miara kąta w stopniach, a kalkulator musi być ustawiony na tryb stopni (degrees), aby obliczyć sinus poprawnie.

Przykład: Romb ma bok długości 7 cm, a jeden z jego kątów ma miarę 30 stopni. Wtedy jego pole wynosi:

P = (7 cm)² * sin(30°) = 49 cm² * 0.5 = 24.5 cm²

4. Pole rombu, znając promień okręgu wpisanego i bok

Romb ma okrąg wpisany, którego promień wynosi r. Znamy też długość boku a. Wówczas pole rombu można obliczyć z następującego wzoru:

P = 2 * a * r

Przykład: Promień okręgu wpisanego w romb wynosi 3 cm, a długość boku rombu to 8 cm. Pole rombu wynosi:

P = 2 * 8 cm * 3 cm = 48 cm²

Praktyczne Zastosowanie Wiedzy o Polu Rombu

Wiedza o obliczaniu pola rombu znajduje zastosowanie w wielu dziedzinach życia i techniki. Oto kilka przykładów:

• Architektura i budownictwo: Projektowanie elewacji budynków, wzorów na podłogach, konstrukcji dachowych.
• Inżynieria: Obliczanie powierzchni elementów konstrukcyjnych, takich jak kratownice.
• Grafika komputerowa: Tworzenie tekstur i wzorów.
• Geodezja: Obliczanie powierzchni działek o kształcie zbliżonym do rombu.
• Sztuka i rzemiosło: Projektowanie biżuterii, mozaik, dekoracji.
• Matematyka i edukacja: Rozwiązywanie zadań geometrycznych, ćwiczenie umiejętności logicznego myślenia.

Wyobraź sobie, że projektujesz parkiet do salonu. Chcesz, aby miał wzór z rombów. Znając wymiary pojedynczego rombu, możesz łatwo obliczyć, ile materiału potrzebujesz do pokrycia całej powierzchni podłogi. Albo, pracując jako architekt, musisz zaprojektować elewację budynku z elementami w kształcie rombów. Znając wymiary rombu, możesz obliczyć, ile materiału fasadowego potrzebujesz i jaki będzie koszt jego zakupu.

Wskazówki i Triki

Oto kilka wskazówek, które mogą ułatwić Ci obliczanie pola rombu:

• Zawsze upewnij się, że jednostki są spójne. Jeśli masz długość w centymetrach i wysokość w metrach, zamień je na tę samą jednostkę przed wykonaniem obliczeń.
• Sprawdź, czy dane są poprawne. Błąd w pomiarze może prowadzić do błędnego wyniku.
• Używaj kalkulatora, aby uniknąć błędów rachunkowych. Szczególnie przy obliczaniu sinusa kąta.
• Narysuj romb, aby lepiej zrozumieć problem. Wizualizacja pomaga w wyborze odpowiedniej metody obliczeń.
• Pamiętaj o różnych wzorach na pole rombu. Wybierz ten, który najlepiej pasuje do dostępnych danych.
• Jeśli masz tylko część danych, postaraj się je obliczyć. Na przykład, jeśli znasz bok rombu i jego przekątną, możesz obliczyć drugą przekątną, wykorzystując twierdzenie Pitagorasa w trójkącie prostokątnym utworzonym przez połowy przekątnych i bok rombu.

Przykładowe Zadania z Rozwiązaniami

Aby jeszcze lepiej utrwalić wiedzę, rozwiążmy kilka przykładowych zadań:

Zadanie 1: Romb ma przekątne o długościach 10 cm i 12 cm. Oblicz jego pole.

Rozwiązanie: Korzystamy ze wzoru P = (d₁ * d₂) / 2. Wstawiamy dane: P = (10 cm * 12 cm) / 2 = 60 cm². Odpowiedź: Pole rombu wynosi 60 cm².

Zadanie 2: Romb ma bok długości 8 cm i wysokość 6 cm. Oblicz jego pole.

Rozwiązanie: Korzystamy ze wzoru P = a * h. Wstawiamy dane: P = 8 cm * 6 cm = 48 cm². Odpowiedź: Pole rombu wynosi 48 cm².

Zadanie 3: Romb ma bok długości 4 cm, a jeden z jego kątów ma miarę 60 stopni. Oblicz jego pole.

Rozwiązanie: Korzystamy ze wzoru P = a² * sin(α). Wstawiamy dane: P = (4 cm)² * sin(60°) = 16 cm² * (√3/2) ≈ 13.86 cm². Odpowiedź: Pole rombu wynosi około 13.86 cm².

Podsumowanie i Wnioski

W tym artykule omówiliśmy różne metody obliczania pola powierzchni rombu. Poznaliśmy wzory oparte na długości przekątnych, długości boku i wysokości, a także długości boku i kąta. Nauczyliśmy się, jak stosować te wzory w praktyce, rozwiązując przykładowe zadania. Mam nadzieję, że teraz obliczanie pola rombu nie sprawi Ci żadnych trudności!

Pamiętaj, że zrozumienie podstawowych zasad geometrii jest kluczowe w wielu dziedzinach. Wykorzystuj zdobytą wiedzę w praktyce, a szybko zauważysz, jak przydatna może być matematyka w codziennym życiu. Powodzenia w dalszej nauce!

Zachęcam Cię do dalszego poszerzania swojej wiedzy z zakresu geometrii i matematyki. Internet jest pełen darmowych zasobów, kursów i materiałów edukacyjnych. Nie bój się eksperymentować i rozwiązywać trudniejszych zadań. Każdy krok naprzód to krok w stronę lepszego zrozumienia świata! Dziękujemy za poświęcony czas!