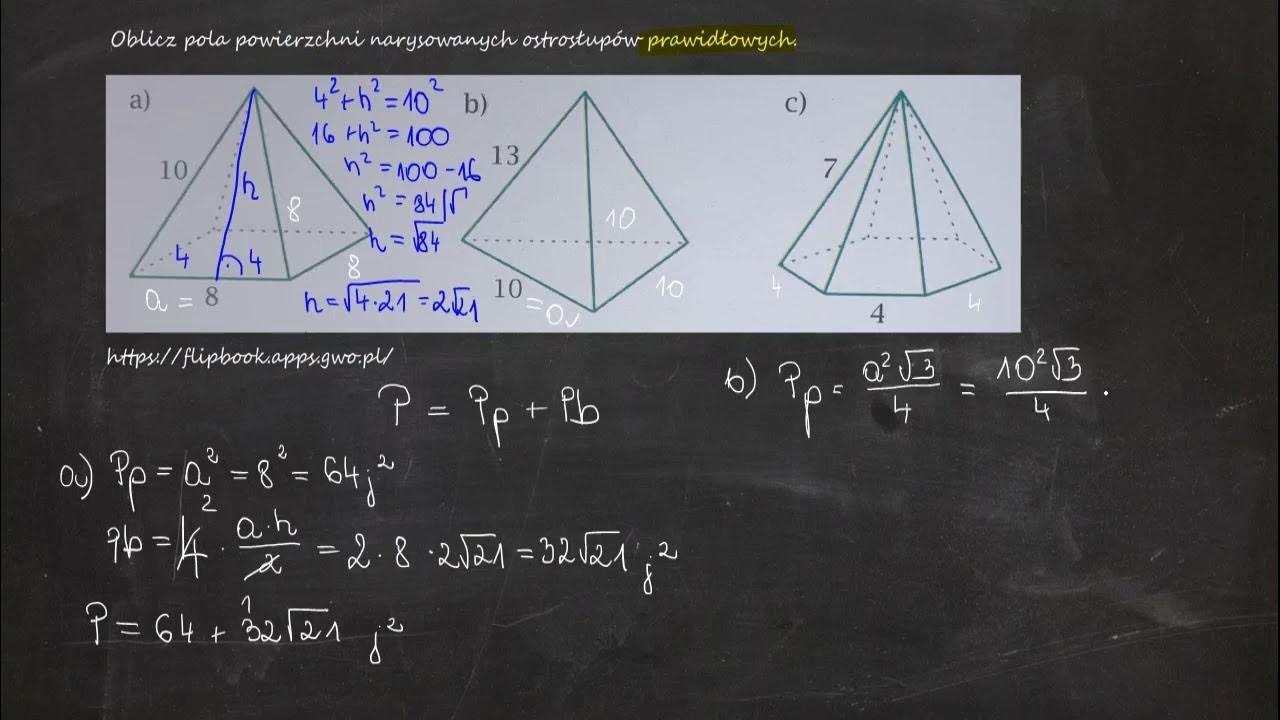
Oblicz Pola Zacieniowanych ścian Ostrosłupa

Czy kiedykolwiek zastanawiałeś się, jak obliczyć pole zacieniowanej ściany ostrosłupa? To zadanie, które na pierwszy rzut oka może wydawać się skomplikowane, ale z odpowiednim podejściem i zrozumieniem podstawowych zasad geometrii, staje się całkiem wykonalne. Wiele osób ma problem z wizualizacją i przełożeniem tego na konkretne obliczenia. Ten artykuł ma na celu rozwianie wszelkich wątpliwości i przedstawienie krok po kroku, jak poradzić sobie z tym wyzwaniem.

Zrozumienie Ostrosłupa i Jego Geometrii

Zanim przejdziemy do obliczeń, warto przypomnieć sobie, czym tak naprawdę jest ostrosłup. To bryła, która ma jedną podstawę (wielokąt) i ściany boczne, które są trójkątami zbiegającymi się w jednym punkcie, zwanym wierzchołkiem ostrosłupa.

Podstawowe elementy ostrosłupa, które musimy znać:

Podstawa: Wielokąt (np. trójkąt, kwadrat, pięciokąt).
Ściany boczne: Trójkąty.
Krawędzie podstawy: Boki wielokąta w podstawie.
Krawędzie boczne: Boki trójkątów ścian bocznych, które łączą wierzchołek ostrosłupa z wierzchołkami podstawy.
Wysokość ostrosłupa: Odcinek prostopadły poprowadzony z wierzchołka ostrosłupa do płaszczyzny podstawy.
Wysokość ściany bocznej (apotema): Odcinek poprowadzony z wierzchołka ostrosłupa prostopadle do krawędzi podstawy ściany bocznej.

Zrozumienie tych elementów jest kluczowe do dalszych obliczeń.

Identyfikacja Zacieniowanej Ściany

Pierwszym krokiem jest identyfikacja zacieniowanej ściany. Często zadanie zawiera rysunek ostrosłupa z zaznaczoną ścianą, której pole mamy obliczyć. Upewnij się, że wiesz, która to ściana – czy jest to jedna ze ścian bocznych, czy podstawa. To fundamentalne dla dalszego procesu.

Sprawdź, czy dana ściana jest trójkątem (ściana boczna) czy wielokątem (podstawa). Informacja ta determinuje wzór, którego będziesz używać.

Obliczanie Pola Ścian Bocznych

Ściany boczne ostrosłupa są trójkątami. Aby obliczyć pole trójkąta, potrzebujemy długości jego podstawy i wysokości.

Wzór na pole trójkąta: P = (1/2) * a * h

Gdzie:

P – pole trójkąta
a – długość podstawy trójkąta (krawędź podstawy ostrosłupa)
h – wysokość trójkąta (wysokość ściany bocznej, czyli apotema)

Przykład: Załóżmy, że mamy ostrosłup prawidłowy czworokątny. Krawędź podstawy ma długość 6 cm, a wysokość ściany bocznej (apotema) wynosi 8 cm. Wtedy pole jednej ściany bocznej wynosi: P = (1/2) * 6 cm * 8 cm = 24 cm².

W przypadku ostrosłupów, które nie są prawidłowe, każda ściana boczna może mieć inną wysokość. Wtedy trzeba obliczyć pole każdej ściany bocznej oddzielnie, używając odpowiedniej podstawy i wysokości dla każdej z nich.

Jak znaleźć wysokość ściany bocznej (apotemę)?

Często wysokość ściany bocznej (apotema) nie jest podana bezpośrednio. Możemy ją obliczyć, korzystając z twierdzenia Pitagorasa, jeśli znamy inne wymiary ostrosłupa (np. wysokość ostrosłupa i połowę długości krawędzi podstawy). Wyobraźmy sobie trójkąt prostokątny, którego przyprostokątne to wysokość ostrosłupa (H) i połowa długości krawędzi podstawy (a/2), a przeciwprostokątna to właśnie apotema (h).

Z twierdzenia Pitagorasa: h² = H² + (a/2)²

Czyli: h = √(H² + (a/2)²)

Przykład: Wysokość ostrosłupa wynosi 4 cm, a krawędź podstawy 6 cm. Wtedy apotema wynosi: h = √(4² + (6/2)²) = √(16 + 9) = √25 = 5 cm.

Obliczanie Pola Podstawy

Pole podstawy zależy od tego, jaki wielokąt tworzy podstawę ostrosłupa. Najczęściej spotykane są trójkąty i kwadraty, ale mogą to być również inne wielokąty foremne.

Trójkąt: P = (1/2) * a * h, gdzie a to długość podstawy trójkąta, a h to wysokość trójkąta.
Kwadrat: P = a², gdzie a to długość boku kwadratu.
Prostokąt: P = a * b, gdzie a i b to długości boków prostokąta.
Wielokąt foremny: P = (n * a² * cot(π/n)) / 4, gdzie n to liczba boków wielokąta, a a to długość boku wielokąta.

Przykład: Jeśli podstawa jest kwadratem o boku 5 cm, to pole podstawy wynosi: P = 5 cm * 5 cm = 25 cm².

Obliczanie Pola Zacieniowanej Ściany, Kiedy Znamy Pole Powierzchni Całkowitej i Pola Innych Ścian.

W niektórych zadaniach możemy znać pole powierzchni całkowitej ostrosłupa i pola wszystkich ścian oprócz tej, której pole chcemy obliczyć. W takim przypadku wystarczy odjąć od pola powierzchni całkowitej sumę pól znanych ścian.

Wzór: P_zacieniowane = P_całkowite - (P_1 + P_2 + ... + P_n)

Gdzie:

P_zacieniowane – pole zacieniowanej ściany
P_całkowite – pole powierzchni całkowitej ostrosłupa
P_1, P_2, ..., P_n – pola pozostałych ścian

Przykład: Pole powierzchni całkowitej ostrosłupa wynosi 100 cm². Znamy pola wszystkich ścian oprócz jednej: 20 cm², 20 cm², 25 cm². Pole zacieniowanej ściany wynosi: P_zacieniowane = 100 cm² - (20 cm² + 20 cm² + 25 cm²) = 100 cm² - 65 cm² = 35 cm².

Kluczowe Wskazówki i Najczęstsze Błędy

Oto kilka kluczowych wskazówek, które pomogą Ci uniknąć błędów:

Zawsze rysuj! Nawet prosty szkic ostrosłupa z zaznaczoną zacieniowaną ścianą pomoże Ci zwizualizować problem.
Sprawdź jednostki! Upewnij się, że wszystkie wymiary są podane w tych samych jednostkach (np. cm, m). Jeśli nie, zamień je.
Uważaj na wzory! Wybierz odpowiedni wzór w zależności od rodzaju ściany (trójkąt, kwadrat, itp.).
Pamiętaj o kolejności działań! Stosuj się do zasad kolejności wykonywania działań (nawiasy, potęgowanie, mnożenie/dzielenie, dodawanie/odejmowanie).
Zrozumienie twierdzenia Pitagorasa jest kluczowe. Wykorzystanie tego twierdzenia do wyznaczenia wysokości ścian bocznych.

Najczęstsze błędy to:

Pomylenie wysokości ostrosłupa z wysokością ściany bocznej (apotemą).
Użycie nieprawidłowego wzoru na pole figury (np. trójkąta).
Błędy w obliczeniach (np. zapominanie o podzieleniu przez 2 w przypadku pola trójkąta).
Brak zamiany jednostek.
Nieprawidłowa identyfikacja zacieniowanej ściany.

Praktyczne Przykłady i Ćwiczenia

Najlepszym sposobem na opanowanie obliczania pola zacieniowanej ściany ostrosłupa jest rozwiązywanie zadań. Spróbuj rozwiązać kilka poniższych przykładów:

Przykład 1: Ostrosłup prawidłowy trójkątny ma krawędź podstawy długości 8 cm i wysokość 10 cm. Oblicz pole jednej ściany bocznej.

Przykład 2: Ostrosłup prawidłowy czworokątny ma krawędź podstawy długości 5 cm i wysokość ściany bocznej 6 cm. Oblicz pole powierzchni całkowitej ostrosłupa.

Przykład 3: Ostrosłup ma pole powierzchni całkowitej 120 cm². Jego podstawa ma pole 30 cm², a dwie ściany boczne mają pola po 25 cm². Oblicz pole trzeciej ściany bocznej.

Rozwiązując te i inne zadania, nabierzesz wprawy i będziesz coraz pewniej radzić sobie z obliczaniem pola zacieniowanej ściany ostrosłupa.

"Geometria jest kluczem do zrozumienia świata. Ucz się jej pilnie, a otworzy przed Tobą drzwi do wielu tajemnic." - Archimedes

Pamiętaj, że kluczem do sukcesu jest praktyka i zrozumienie podstawowych zasad. Nie zrażaj się początkowymi trudnościami. Z każdym rozwiązanym zadaniem będziesz bliżej opanowania tej umiejętności. Powodzenia!