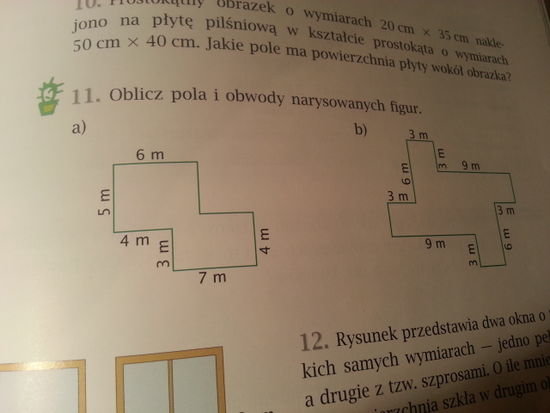
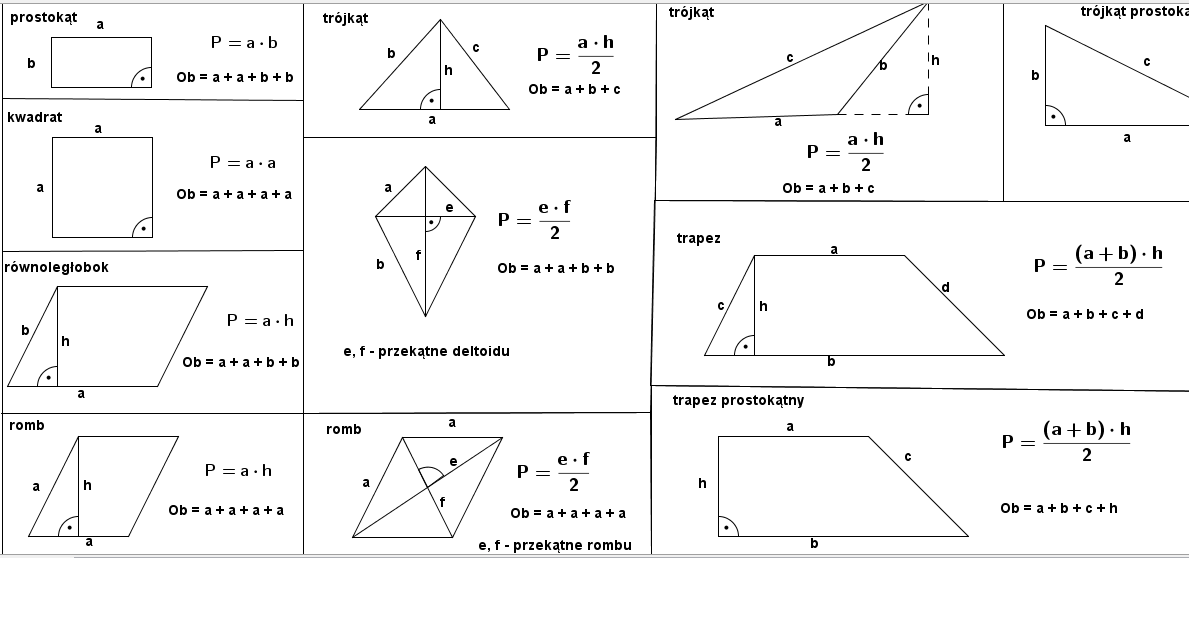
Oblicz Pola I Obwody Narysowanych Figur

Drodzy nauczyciele i edukatorzy matematyki,

Ten artykuł ma na celu wsparcie Was w procesie nauczania zagadnienia obliczania pól i obwodów narysowanych figur geometrycznych. To fundament geometrii, który otwiera drzwi do bardziej zaawansowanych koncepcji. Przedstawię tutaj wskazówki, jak efektywnie tłumaczyć te zagadnienia, rozwiewać typowe wątpliwości uczniów i uczynić naukę bardziej angażującą.

Wprowadzenie do zagadnienia pól i obwodów

Zanim przejdziemy do bardziej złożonych kształtów, upewnijcie się, że uczniowie rozumieją podstawowe definicje. Pole figury to miara powierzchni, którą ta figura zajmuje. Wyobraźcie sobie, że malujecie figurę – pole to ilość farby potrzebna do jej pokrycia. Z kolei obwód figury to suma długości wszystkich jej boków. Pomyślcie o ogrodzeniu wokół działki – obwód to długość tego ogrodzenia.

Kluczowe figury i ich wzory

Rozpocznijcie od najprostszych figur: kwadratu, prostokąta, trójkąta i koła. Ważne jest, aby uczniowie nie tylko znali wzory na pamięć, ale także rozumieli skąd się one biorą. Na przykład:

Kwadrat: Pole = bok * bok (a²), Obwód = 4 * bok (4a)
Prostokąt: Pole = długość * szerokość (a * b), Obwód = 2 * (długość + szerokość) (2(a+b))
Trójkąt: Pole = 1/2 * podstawa * wysokość (½ * a * h), Obwód = suma długości boków (a+b+c)
Koło: Pole = π * promień² (πr²), Obwód (długość okręgu) = 2 * π * promień (2πr)

Poświęćcie czas na wyjaśnienie, co oznaczają poszczególne symbole (a, b, h, r, π) i jakie są ich jednostki miary (cm, m, km, cm², m², km²).

Praktyczne wskazówki dla nauczycieli

Wizualizacja: Używajcie modeli 3D, rysunków, a nawet oprogramowania do geometrii, aby uczniowie mogli zobaczyć figury w różnych perspektywach.
Praktyka: Dajcie uczniom dużo zadań praktycznych. Zacznijcie od prostych, a następnie stopniowo zwiększajcie trudność.
Przykłady z życia: Pokażcie uczniom, jak obliczanie pól i obwodów jest przydatne w życiu codziennym. Na przykład, obliczanie powierzchni pokoju przy kupnie dywanu lub obwodu działki przy budowie ogrodzenia.
Praca w grupach: Zachęcajcie uczniów do pracy w grupach, aby mogli wymieniać się wiedzą i pomagać sobie nawzajem.
Wykorzystanie technologii: Używajcie kalkulatorów i arkuszy kalkulacyjnych, aby uczniowie mogli skupić się na rozumieniu koncepcji, a nie na żmudnych obliczeniach.

Rozwiązywanie typowych problemów i rozwiewanie wątpliwości

Uczniowie często mają problemy z następującymi aspektami:

Jednostki miary: Mylą jednostki długości z jednostkami powierzchni. Podkreślajcie, że obwód jest mierzony w jednostkach długości (cm, m, km), a pole w jednostkach powierzchni (cm², m², km²).
Wysokość w trójkącie: Często mylą wysokość z długością boku. Wyjaśnijcie, że wysokość to odcinek prostopadły do podstawy, opuszczony z wierzchołka.
Pi (π): Nie rozumieją, czym jest liczba Pi i dlaczego jest używana w obliczeniach związanych z kołem. Wyjaśnijcie, że Pi to stosunek obwodu koła do jego średnicy, i że jest to liczba niewymierna (w przybliżeniu 3.14).
Figury złożone: Mają trudności z obliczaniem pól i obwodów figur złożonych, które składają się z kilku prostszych figur. Podzielcie figurę złożoną na prostsze elementy, obliczcie pola i obwody każdego elementu oddzielnie, a następnie zsumujcie wyniki.
Brakujące dane: Często nie wiedzą, jak obliczyć pole lub obwód, gdy brakuje niektórych danych. Nauczcie ich, jak wykorzystywać dostępne informacje i wiedzę o właściwościach figur, aby znaleźć brakujące dane. Na przykład, użycie twierdzenia Pitagorasa w trójkącie prostokątnym.

Błędy w obliczeniach wynikają często z nieuwagi. Nauczcie uczniów sprawdzania jednostek i wyników obliczeń.

Jak uczynić naukę bardziej angażującą?

Oto kilka pomysłów na uatrakcyjnienie lekcji:

Gry edukacyjne: Wykorzystajcie gry online lub stwórzcie własne gry planszowe, które będą wymagały obliczania pól i obwodów.
Projekty praktyczne: Zorganizujcie projekt, w którym uczniowie będą musieli zaprojektować ogród, pokój lub inny obiekt, a następnie obliczyć jego pole i obwód.
Zadania z elementami rywalizacji: Zorganizujcie konkurs na najszybsze i najdokładniejsze obliczenie pól i obwodów różnych figur.
Wykorzystanie technologii: Używajcie aplikacji i programów, które pozwalają na interaktywne rozwiązywanie zadań i eksperymentowanie z różnymi figurami geometrycznymi.
"Poszukiwanie skarbów": Stwórzcie grę terenową, w której uczniowie będą musieli rozwiązywać zadania związane z polami i obwodami, aby znaleźć ukryty skarb.

Przykładowo, możecie poprosić uczniów o:

"Obliczenie pola powierzchni klasy. Uczniowie muszą zmierzyć długość i szerokość klasy, a następnie obliczyć pole. Możecie to urozmaicić, prosząc o oszacowanie kosztu położenia nowych płytek na podłodze."

Podsumowanie

Nauczanie obliczania pól i obwodów to kluczowy element edukacji matematycznej. Pamiętajcie, aby zaczynać od podstaw, tłumaczyć koncepcje w sposób zrozumiały dla uczniów, dawać dużo przykładów i zadań praktycznych, a także wykorzystywać różnorodne metody nauczania, aby uatrakcyjnić lekcje. Rozwiewajcie wątpliwości i pokazujcie zastosowanie tych umiejętności w życiu codziennym. Dzięki temu uczniowie nie tylko zapamiętają wzory, ale także zrozumieją, jak je stosować i docenią piękno geometrii.

Życzę powodzenia w pracy z uczniami!