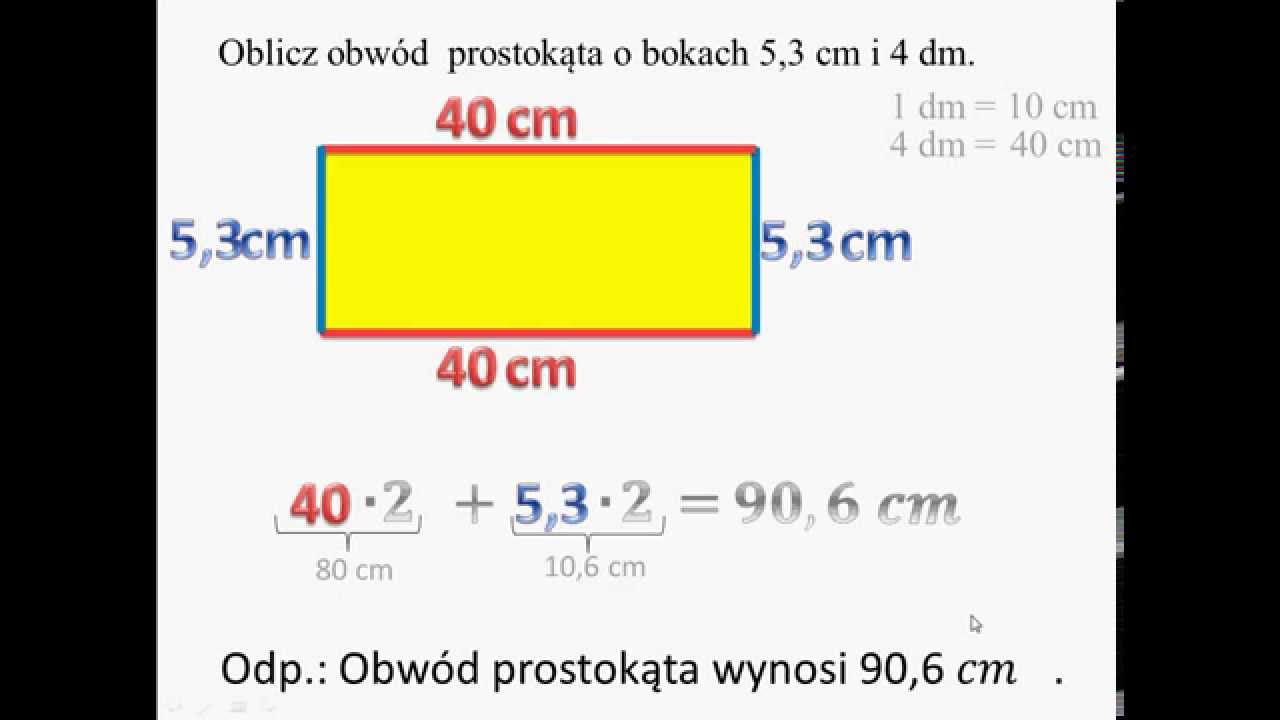
Oblicz Obwód Prostokąta O Bokach

W życiu codziennym często spotykamy się z różnymi kształtami geometrycznymi, a jednym z najprostszych i najpopularniejszych jest prostokąt. Zrozumienie jego właściwości, w tym jak obliczyć jego obwód, jest niezwykle przydatne, nie tylko w szkole, ale i w wielu praktycznych sytuacjach.

Czym jest Prostokąt?

Prostokąt to czworokąt, który ma dwie pary boków równoległych i równej długości oraz wszystkie kąty proste (90 stopni). Oznacza to, że ma dwa boki oznaczane jako długość (często oznaczane jako 'a') i dwa boki oznaczane jako szerokość (często oznaczane jako 'b'). Kwadrat jest szczególnym przypadkiem prostokąta, gdzie wszystkie boki mają jednakową długość.

Definicja i Właściwości Kluczowe

Aby w pełni zrozumieć obliczanie obwodu prostokąta, musimy przypomnieć sobie jego podstawowe cechy:

• Dwie pary boków równoległych: boki przeciwległe są równoległe i mają taką samą długość.
• Wszystkie kąty proste: każdy kąt wewnętrzny prostokąta ma miarę 90 stopni.
• Przekątne: Przekątne prostokąta są równe i przecinają się w połowie.

Obwód Prostokąta: Definicja i Formuła

Obwód dowolnej figury geometrycznej to suma długości wszystkich jej boków. W przypadku prostokąta, obwód to suma dwóch długości i dwóch szerokości.

Wyjaśnienie Formuły

Oznaczając długość prostokąta jako 'a' i szerokość jako 'b', formuła na obwód (O) prostokąta wygląda następująco:

O = 2a + 2b

Możemy również zapisać to jako:

O = 2 * (a + b)

Obie formy są równoważne i pozwalają na szybkie i efektywne obliczenie obwodu, znając długość i szerokość prostokąta.

Przykład Obliczeniowy

Załóżmy, że mamy prostokąt o długości 5 cm i szerokości 3 cm. Jak obliczyć jego obwód?

Używając formuły O = 2a + 2b:

O = 2 * 5 cm + 2 * 3 cm

O = 10 cm + 6 cm

O = 16 cm

Zatem obwód tego prostokąta wynosi 16 cm.

Krok po Kroku: Jak Obliczyć Obwód Prostokąta

Obliczenie obwodu prostokąta jest proste, jeśli postępujesz zgodnie z następującymi krokami:

1. Zidentyfikuj długość (a) i szerokość (b) prostokąta. Upewnij się, że obie wartości są podane w tej samej jednostce (np. cm, metry, cale).
2. Podstaw wartości a i b do wzoru: O = 2a + 2b lub O = 2 * (a + b).
3. Wykonaj obliczenia: Najpierw pomnóż długość i szerokość przez 2, a następnie dodaj wyniki. Alternatywnie, dodaj długość i szerokość, a następnie pomnóż sumę przez 2.
4. Podaj wynik: Pamiętaj o podaniu jednostki długości (np. cm, m, cal).

Przykłady Zastosowania w Życiu Codziennym

Obliczanie obwodu prostokąta ma wiele praktycznych zastosowań:

Ogród i Działka

Wyobraź sobie, że chcesz ogrodzić swój ogródek warzywny, który ma kształt prostokąta. Znając długość i szerokość ogródka, możesz łatwo obliczyć, ile metrów siatki potrzebujesz.

Na przykład, jeśli ogródek ma wymiary 8 metrów długości i 5 metrów szerokości, potrzebujesz:

O = 2 * 8 m + 2 * 5 m = 16 m + 10 m = 26 metrów siatki.

Rama Obrazu

Chcesz oprawić obraz w ramę. Aby kupić odpowiednią ilość materiału na ramę, musisz obliczyć obwód obrazu.

Jeśli obraz ma wymiary 30 cm na 40 cm, to:

O = 2 * 30 cm + 2 * 40 cm = 60 cm + 80 cm = 140 cm.

Budowa i Remont

Podczas planowania remontu pokoju, możesz chcieć obliczyć, ile listew przypodłogowych potrzebujesz, aby je zamontować wzdłuż ścian. Pokój ma zazwyczaj kształt prostokąta.

Architektura i Projektowanie Wnętrz

Architekci i projektanci wnętrz nieustannie wykorzystują obliczenia obwodów przy planowaniu układu pomieszczeń, doboru materiałów i szacowaniu kosztów. Na przykład, obliczenie obwodu pomieszczenia pozwala na oszacowanie potrzebnej ilości tapety lub farby.

Częste Błędy i Jak ich Unikać

Podczas obliczania obwodu prostokąta, można popełnić kilka typowych błędów:

• Używanie różnych jednostek: Upewnij się, że długość i szerokość są wyrażone w tej samej jednostce. Jeśli jedna jest w centymetrach, a druga w metrach, najpierw przekształć je do tej samej jednostki.
• Zapominanie o pomnożeniu przez 2: Pamiętaj, że obwód to suma dwóch długości i dwóch szerokości.
• Błędne podstawianie wartości: Uważaj, żeby nie pomylić długości z szerokością.
• Nieprawidłowe obliczenia arytmetyczne: Sprawdź dokładnie swoje obliczenia, aby uniknąć prostych pomyłek.

Złożone Scenariusze i Rozwiązania

Czasami możemy spotkać się z bardziej skomplikowanymi sytuacjami, gdzie obliczenie obwodu prostokąta wymaga dodatkowych kroków.

Brakujące Dane

Co, jeśli znamy tylko jedną długość boku i pole powierzchni prostokąta? Musimy najpierw obliczyć brakujący bok, a następnie użyć go do obliczenia obwodu.

Na przykład, jeśli pole prostokąta wynosi 24 cm², a długość jednego z boków to 6 cm, to szerokość (b) obliczamy jako:

Pole = a * b => b = Pole / a = 24 cm² / 6 cm = 4 cm.

Teraz możemy obliczyć obwód:

O = 2 * 6 cm + 2 * 4 cm = 12 cm + 8 cm = 20 cm.

Prostokąty Złożone

W niektórych przypadkach, możemy mieć do czynienia z figurami, które są złożone z kilku prostokątów. Wtedy musimy podzielić figurę na prostokąty składowe, obliczyć obwód każdego z nich, a następnie dodać długości odpowiednich boków, pamiętając o odjęciu boków, które nie stanowią zewnętrznego obwodu całej figury.

Narzędzia Pomocne w Obliczeniach

W dzisiejszych czasach mamy dostęp do wielu narzędzi, które ułatwiają obliczanie obwodu prostokąta:

• Kalkulatory online: Istnieją liczne kalkulatory online, które automatycznie obliczają obwód, wystarczy podać długość i szerokość.
• Aplikacje mobilne: Wiele aplikacji na smartfony oferuje funkcje obliczania różnych parametrów geometrycznych, w tym obwodu prostokąta.
• Programy komputerowe: Programy CAD i inne programy do projektowania często posiadają funkcje automatycznego obliczania obwodów różnych figur.

Podsumowanie i Zachęta do Dalszej Nauki

Obliczanie obwodu prostokąta to podstawowa umiejętność matematyczna, która znajduje szerokie zastosowanie w życiu codziennym. Zrozumienie definicji, wzoru i sposobu obliczania obwodu, a także unikanie typowych błędów, pozwala na efektywne rozwiązywanie problemów praktycznych. Pamiętaj, praktyka czyni mistrza! Im więcej przykładów rozwiążesz, tym pewniej będziesz się czuć w obliczeniach geometrycznych.

Zachęcam do dalszego zgłębiania wiedzy z zakresu geometrii. Poznawanie kolejnych figur geometrycznych i ich właściwości poszerzy Twoje umiejętności i otworzy Ci drzwi do fascynującego świata matematyki i jej zastosowań.