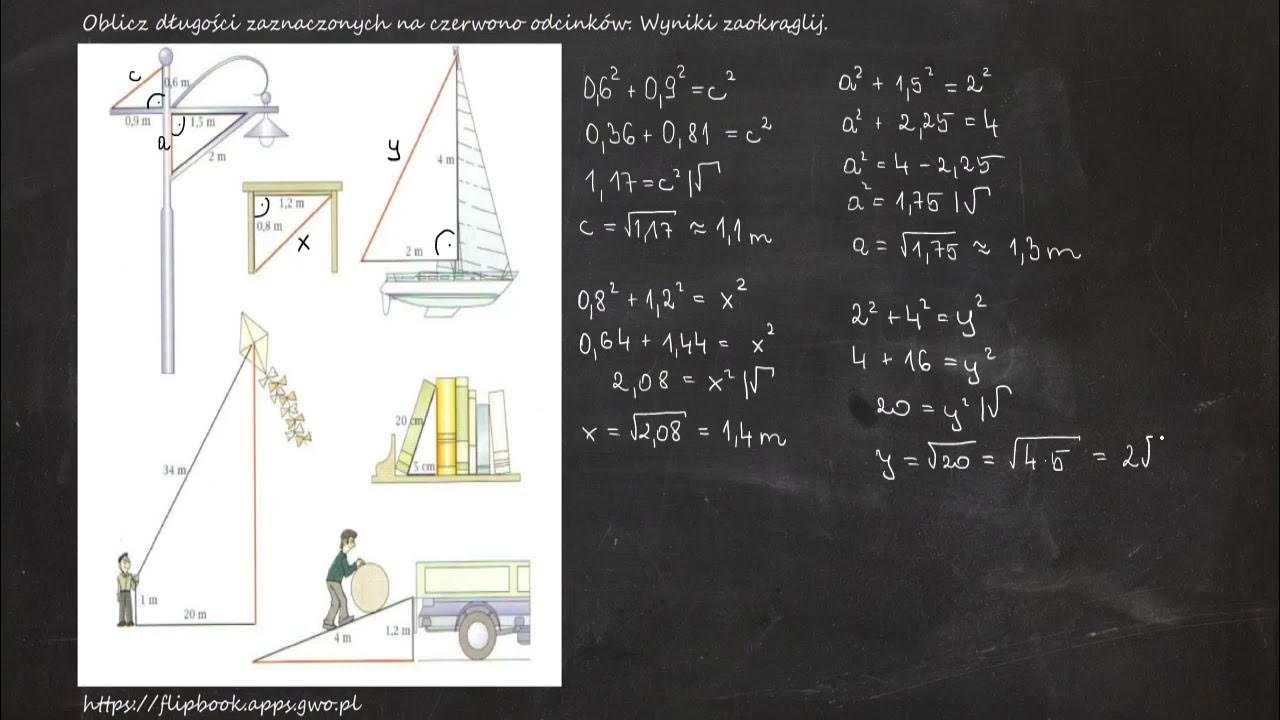
Oblicz Długości Zaznaczonych Na Czerwono Odcinków Wyniki Zaokrąglij

Hej! Dziś zajmiemy się obliczaniem długości odcinków zaznaczonych na czerwono, a potem zaokrąglimy wyniki. Brzmi strasznie? Spokojnie, rozłożymy to na czynniki pierwsze i zobaczycie, że to wcale nie jest takie trudne! Myślcie o tym jak o układance, gdzie mamy pewne elementy, i musimy znaleźć brakujący kawałek.

Dlaczego to robimy? Czyli po co nam te odcinki?

Może się zastanawiacie: "Po co w ogóle obliczać te długości?". Wyobraźcie sobie, że projektujecie pokój. Chcecie kupić dywan, który idealnie pasuje pod stolik. Musiecie znać wymiary podłogi (odcinki!), żeby dywan nie był za mały, ani za duży. Albo, że budujecie domek dla ptaków. Musicie wiedzieć, jak długie deski pociąć. Długości odcinków są potrzebne w wielu realnych sytuacjach – w budownictwie, projektowaniu, kartografii, a nawet w grach komputerowych!

Inny przykład? GPS w samochodzie! Żeby nawigacja pokazała najkrótszą drogę, musi obliczyć odległości między różnymi punktami na mapie – czyli, zgadliście, długości odcinków!

Narzędzia do naszej układanki: Geometria w akcji!

Do obliczania długości odcinków zaznaczonych na czerwono najczęściej używamy wiedzy z geometrii. Kluczowe są następujące pojęcia:

• Twierdzenie Pitagorasa: Brzmi groźnie, ale jest bardzo proste! Stosujemy je w trójkątach prostokątnych. Pamiętajcie: trójkąt prostokątny to taki, który ma jeden kąt prosty (90 stopni). Twierdzenie Pitagorasa mówi, że: a² + b² = c², gdzie "a" i "b" to długości przyprostokątnych (boki przyległe do kąta prostego), a "c" to długość przeciwprostokątnej (bok naprzeciwko kąta prostego). Wyobraźcie sobie, że "c" to najdłuższa ślizgawka na placu zabaw, a "a" i "b" to drabinki, po których trzeba się wspiąć.
• Funkcje trygonometryczne: Sinus, cosinus i tangens. To takie magiczne narzędzia, które łączą kąty w trójkącie z długościami jego boków. Działają w trójkątach prostokątnych. Sinus kąta to stosunek długości boku naprzeciwko kąta do długości przeciwprostokątnej. Cosinus to stosunek długości boku przyległego do kąta do długości przeciwprostokątnej. Tangens to stosunek długości boku naprzeciwko kąta do długości boku przyległego do kąta. Można zapamiętać to za pomocą mnemotechniki: SOH CAH TOA (Sinus-Opposite-Hypotenuse, Cosinus-Adjacent-Hypotenuse, Tangent-Opposite-Adjacent). Pomyślcie o tym, jak o specjalnych "kodach", które tłumaczą nam, jak kąty wpływają na długość boków.
• Podobieństwo trójkątów: Jeśli mamy dwa trójkąty, które mają takie same kąty (są podobne), to stosunki długości ich odpowiadających boków są równe. Wyobraźcie sobie dwa zdjęcia tego samego budynku – jedno małe, a drugie duże. Budynek jest ten sam (te same kąty!), tylko w innej skali. Podobieństwo trójkątów pozwala nam przeliczać długości boków między tymi "zdjęciami".
• Równoległoboki i inne figury: Często odcinki, których długości szukamy, są częścią bardziej skomplikowanych figur, takich jak równoległoboki, trapezy czy romby. Wtedy musimy wykorzystać właściwości tych figur, żeby znaleźć relacje między odcinkami. Na przykład, w równoległoboku przeciwległe boki są równe i równoległe.

Przykład krok po kroku: Używamy Twierdzenia Pitagorasa!

Załóżmy, że mamy trójkąt prostokątny, gdzie jedna przyprostokątna ma długość 3 cm, druga ma długość 4 cm, a my chcemy obliczyć długość przeciwprostokątnej (odcinek zaznaczony na czerwono).

1. Zidentyfikuj: Widzimy, że mamy trójkąt prostokątny, więc możemy użyć Twierdzenia Pitagorasa. Oznaczmy przyprostokątne jako a = 3 cm i b = 4 cm, a przeciwprostokątną (szukany odcinek) jako c.
2. Podstaw: Podstawiamy wartości do wzoru: 3² + 4² = c²
3. Oblicz: 9 + 16 = c² czyli 25 = c²
4. Pierwiastek: Żeby znaleźć "c", musimy obliczyć pierwiastek kwadratowy z 25. Pierwiastek kwadratowy z 25 to 5.
5. Wniosek: Długość przeciwprostokątnej (odcinek zaznaczony na czerwono) wynosi 5 cm.

Zaokrąglanie wyników: Trochę precyzji!

Po obliczeniu długości odcinka często trzeba zaokrąglić wynik. Zaokrąglamy po to, żeby uprościć liczbę i żeby była bardziej praktyczna. Na przykład, wynik 3.14159265... jest bardzo dokładny, ale w większości sytuacji wystarczy zaokrąglić go do 3.14. Ważne jest, żeby znać zasady zaokrąglania. Jeśli cyfra, którą odrzucamy, jest mniejsza niż 5, to poprzednia cyfra pozostaje bez zmian. Jeśli cyfra, którą odrzucamy, jest większa lub równa 5, to poprzednia cyfra zwiększa się o 1. Na przykład, 3.141 zaokrąglone do dwóch miejsc po przecinku to 3.14, a 3.145 zaokrąglone do dwóch miejsc po przecinku to 3.15.

Spójrzmy na nasz poprzedni przykład. Obliczyliśmy, że długość przeciwprostokątnej wynosi 5 cm. Jeżeli po dalszych obliczeniach wynik okazałby się 5.237 cm, a polecenie brzmi "zaokrąglij do jednego miejsca po przecinku", to zaokrąglilibyśmy do 5.2 cm, ponieważ cyfra po "3" to "7", czyli jest większa niż 5. Jeżeli wynik byłby 5.232 cm, to zaokrąglilibyśmy do 5.2 cm, ponieważ cyfra po "3" to "2", czyli jest mniejsza niż 5.

Pamiętajcie, żeby zawsze sprawdzić, do ilu miejsc po przecinku należy zaokrąglić wynik! Informacja ta powinna być zawarta w treści zadania.

Wskazówki dla wzrokowców:

• Rysuj! Zawsze rysuj sobie diagram, żeby zobaczyć, jak wyglądają odcinki i jakie relacje między nimi zachodzą.
• Koloruj! Używaj różnych kolorów, żeby zaznaczyć różne elementy w zadaniu. Na przykład, zaznacz odcinki, których długości szukasz na czerwono, a znane długości na niebiesko.
• Używaj symboli: Oznaczaj kąty i boki literami, żeby łatwiej było się odwoływać do nich w obliczeniach.
• Szukaj podobieństw: Czy widzisz jakieś znane figury w zadaniu? Czy możesz podzielić skomplikowaną figurę na prostsze elementy, takie jak trójkąty?

Pamiętajcie, praktyka czyni mistrza! Im więcej zadań rozwiążecie, tym łatwiej będzie wam obliczać długości odcinków zaznaczonych na czerwono i zaokrąglać wyniki. Powodzenia!