Nwd I Nww Zadania Klasa 5

Cześć! Pewnie trafiłeś tutaj, bo NWD i NWW w klasie 5 wydają Ci się czarną magią. Nie martw się, to normalne! Wielu uczniów ma z tym trudności. Zadania z NWD i NWW potrafią być naprawdę zagmatwane, a pojęcia brzmią dość tajemniczo. Ale obiecuję, że wspólnie spróbujemy je zrozumieć, krok po kroku.

Spróbujmy spojrzeć na to z innej strony. Wyobraź sobie, że organizujesz urodziny i chcesz podzielić cukierki i ciastka tak, aby każdy dostał po równo i nic nie zostało. Albo, że chcesz ułożyć klocki LEGO w jednakowe wieże. NWD i NWW pomagają nam rozwiązywać właśnie takie problemy! To narzędzia, które ułatwiają dzielenie i grupowanie.

Zatem, bez zbędnych wstępów, przejdźmy do konkretów!

Co to jest NWD i NWW?

Zanim zaczniemy rozwiązywać zadania, musimy najpierw zrozumieć, czym właściwie są NWD i NWW:

NWD – Największy Wspólny Dzielnik

NWD, czyli Największy Wspólny Dzielnik, to największa liczba, przez którą można podzielić dwie (lub więcej) liczby bez reszty. Brzmi skomplikowanie? Spójrzmy na przykład:

Weźmy liczby 12 i 18. Jakie są ich dzielniki?

Dzielniki liczby 12: 1, 2, 3, 4, 6, 12
Dzielniki liczby 18: 1, 2, 3, 6, 9, 18

Widzimy, że obie liczby mają wspólne dzielniki: 1, 2, 3 i 6. Ale który z nich jest największy? Oczywiście 6! Zatem NWD(12, 18) = 6.

Czyli NWD to taka "największa siła", która dzieli dwie liczby na równe części.

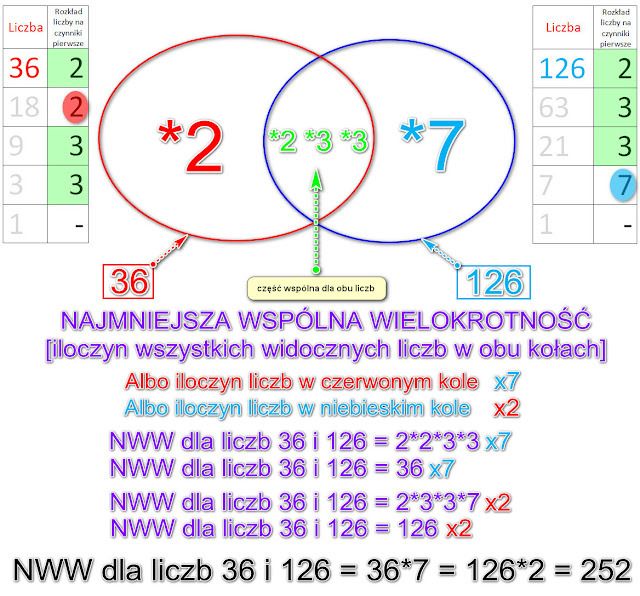
NWW – Najmniejsza Wspólna Wielokrotność

NWW, czyli Najmniejsza Wspólna Wielokrotność, to najmniejsza liczba, która jest wielokrotnością dwóch (lub więcej) liczb. Znów brzmi enigmatycznie? Przykład wszystko wyjaśni:

Weźmy liczby 4 i 6. Jakie są ich wielokrotności?

Wielokrotności liczby 4: 4, 8, 12, 16, 20, 24, 28, 32, 36...
Wielokrotności liczby 6: 6, 12, 18, 24, 30, 36, 42...

Widzimy, że obie liczby mają wspólne wielokrotności: 12, 24, 36... Ale która z nich jest najmniejsza? Oczywiście 12! Zatem NWW(4, 6) = 12.

NWW to taka "najmniejsza meta", do której obie liczby dążą przez mnożenie.

Jak obliczyć NWD i NWW?

Istnieje kilka metod obliczania NWD i NWW. Dwie najpopularniejsze to:

Metoda wypisywania dzielników/wielokrotności

Tak jak pokazaliśmy w przykładach powyżej, możemy po prostu wypisać dzielniki (dla NWD) lub wielokrotności (dla NWW) obu liczb i znaleźć odpowiednio największy wspólny dzielnik lub najmniejszą wspólną wielokrotność. Ta metoda jest dobra dla małych liczb, ale przy większych liczbach robi się żmudna.

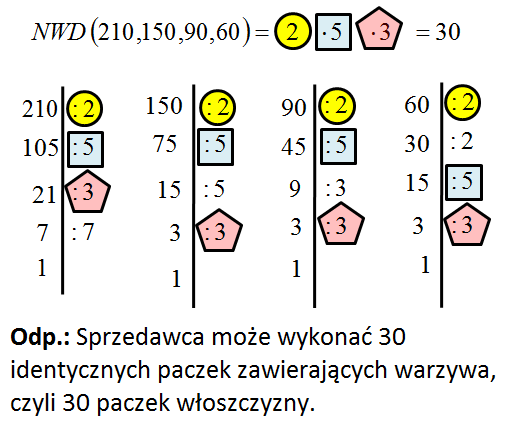
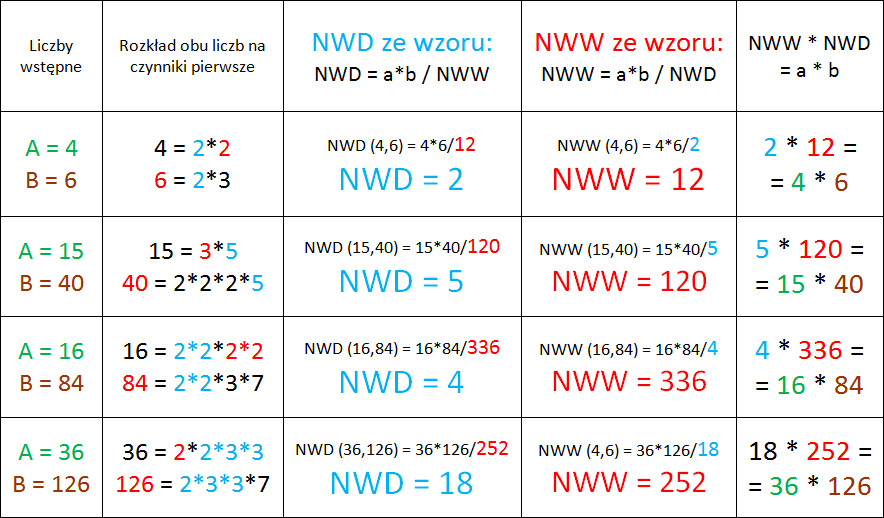
Metoda rozkładu na czynniki pierwsze

Ta metoda jest bardziej uniwersalna i przydatna, zwłaszcza przy większych liczbach. Polega na rozłożeniu każdej liczby na czynniki pierwsze (czyli liczby, które dzielą się tylko przez 1 i przez samą siebie, np. 2, 3, 5, 7, 11...).

Przykład NWD: Oblicz NWD(36, 48)

Rozkładamy liczby na czynniki pierwsze:
- 36 = 2 * 2 * 3 * 3 = 2² * 3²
- 48 = 2 * 2 * 2 * 2 * 3 = 2⁴ * 3
Wybieramy wspólne czynniki pierwsze z najmniejszymi potęgami:
- Wspólne czynniki to 2 i 3.
- Najmniejsza potęga 2 to 2².
- Najmniejsza potęga 3 to 3¹.
Mnożymy wybrane czynniki:
- NWD(36, 48) = 2² * 3 = 4 * 3 = 12

Przykład NWW: Oblicz NWW(15, 20)

Rozkładamy liczby na czynniki pierwsze:
- 15 = 3 * 5
- 20 = 2 * 2 * 5 = 2² * 5
Wybieramy wszystkie czynniki pierwsze z największymi potęgami:
- Wszystkie czynniki to 2, 3 i 5.
- Największa potęga 2 to 2².
- Największa potęga 3 to 3¹.
- Największa potęga 5 to 5¹.
Mnożymy wybrane czynniki:
- NWW(15, 20) = 2² * 3 * 5 = 4 * 3 * 5 = 60

Przykładowe zadania i ich rozwiązania

Teraz czas na praktykę! Rozwiążmy kilka zadań, używając omówionych metod.

Zadanie 1: Dwie koleżanki, Kasia i Basia, zbierają znaczki. Kasia ma 24 znaczki z Polski i 36 znaczków z zagranicy. Chcą podzielić znaczki na paczki, tak aby każda paczka zawierała tyle samo znaczków z Polski i tyle samo znaczków z zagranicy. Ile najwięcej paczek mogą utworzyć i ile znaczków z każdego rodzaju będzie w każdej paczce?

Rozwiązanie:

Musimy znaleźć NWD(24, 36), ponieważ to nam powie, ile najwięcej paczek możemy utworzyć.

Rozkład na czynniki pierwsze:
- 24 = 2 * 2 * 2 * 3 = 2³ * 3
- 36 = 2 * 2 * 3 * 3 = 2² * 3²
Wspólne czynniki z najmniejszymi potęgami:
- 2² i 3
NWD(24, 36) = 2² * 3 = 4 * 3 = 12

Odp: Mogą utworzyć 12 paczek. W każdej paczce będzie 24/12 = 2 znaczki z Polski i 36/12 = 3 znaczki z zagranicy.

Zadanie 2: Dwa autobusy wyruszają z tego samego przystanku. Pierwszy autobus kursuje co 15 minut, a drugi co 20 minut. Po ilu minutach autobusy znów spotkają się na przystanku?

Rozwiązanie:

Musimy znaleźć NWW(15, 20), ponieważ to nam powie, po ilu minutach się spotkają.

Rozkład na czynniki pierwsze:
- 15 = 3 * 5
- 20 = 2 * 2 * 5 = 2² * 5
Wszystkie czynniki z największymi potęgami:
- 2², 3 i 5
NWW(15, 20) = 2² * 3 * 5 = 4 * 3 * 5 = 60

Odp: Autobusy spotkają się ponownie na przystanku po 60 minutach.

Zadanie 3: Znajdź NWD(18, 24, 30)

Rozwiązanie:

Rozkład na czynniki pierwsze:
- 18 = 2 * 3 * 3 = 2 * 3²
- 24 = 2 * 2 * 2 * 3 = 2³ * 3
- 30 = 2 * 3 * 5
Wspólne czynniki z najmniejszymi potęgami:
- 2 i 3
NWD(18, 24, 30) = 2 * 3 = 6

Odp: NWD(18, 24, 30) = 6.

Częste błędy i jak ich unikać

Rozwiązując zadania z NWD i NWW, łatwo o pomyłkę. Oto kilka częstych błędów i wskazówki, jak ich unikać:

Pomylenie NWD z NWW: Pamiętaj, że NWD szukamy największego dzielnika, a NWW – najmniejszej wielokrotności. Zastanów się, co jest logiczne w kontekście zadania.
Błędy w rozkładzie na czynniki pierwsze: Sprawdź dokładnie, czy dobrze rozłożyłeś liczby na czynniki pierwsze. Czasami łatwo zapomnieć o jakimś czynniku.
Wybór nieodpowiednich potęg: Przy NWD wybieramy czynniki z najmniejszymi potęgami, a przy NWW – z największymi.
Zapominanie o zerze: Zero jest wielokrotnością każdej liczby, ale nie ma dzielników (poza 1, jeśli przyjmiemy taką definicję), więc nie uwzględniamy go przy obliczeniach.

Dlaczego to jest ważne?

Może się zastanawiasz, po co w ogóle uczymy się o NWD i NWW. Przecież nie będziemy tego używać w życiu codziennym, prawda? Otóż, wbrew pozorom, NWD i NWW mają wiele zastosowań w różnych dziedzinach życia.

Wyobraź sobie, że jesteś architektem i projektujesz układanie płytek na podłodze. Musisz wybrać takie płytki, żeby cała podłoga była pokryta bez konieczności docinania płytek. NWD pomaga w znalezieniu odpowiednich wymiarów płytek.

Albo jesteś programistą i piszesz program, który ma synchronizować dane z różnych źródeł. NWW pomaga w ustaleniu, jak często program ma wykonywać synchronizację, aby uniknąć konfliktów.

NWD i NWW są też przydatne w matematyce wyższej, na przykład w teorii liczb czy kryptografii. Zatem, choć może się to nie wydawać, ucząc się o NWD i NWW, inwestujesz w swoją przyszłość!

Niektórzy mogą argumentować, że w dobie kalkulatorów i komputerów nie ma sensu uczyć się obliczania NWD i NWW ręcznie. Skoro masz narzędzie, które to robi za Ciebie, po co się męczyć? To prawda, że kalkulatory i komputery ułatwiają nam życie, ale zrozumienie idei NWD i NWW jest ważne, aby móc efektywnie korzystać z tych narzędzi i rozwiązywać problemy, które wymagają logicznego myślenia.

Pamiętaj, że matematyka to nie tylko obliczenia, ale przede wszystkim sposób myślenia.

Podsumowanie

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, czym są NWD i NWW i jak rozwiązywać zadania z nimi związane. Pamiętaj, że kluczem do sukcesu jest praktyka. Im więcej zadań rozwiążesz, tym lepiej zrozumiesz te pojęcia i tym łatwiej będzie Ci radzić sobie z trudniejszymi problemami.

Spróbuj rozwiązywać zadania samodzielnie, analizuj swoje błędy i nie zrażaj się niepowodzeniami. Każdy kiedyś zaczynał. Możesz również poszukać dodatkowych materiałów w internecie, w podręcznikach lub poprosić o pomoc nauczyciela lub kolegów.

I na koniec: czy po przeczytaniu tego artykułu czujesz się pewniej w rozwiązywaniu zadań z NWD i NWW? Jakie zadanie spróbujesz rozwiązać jako następne?