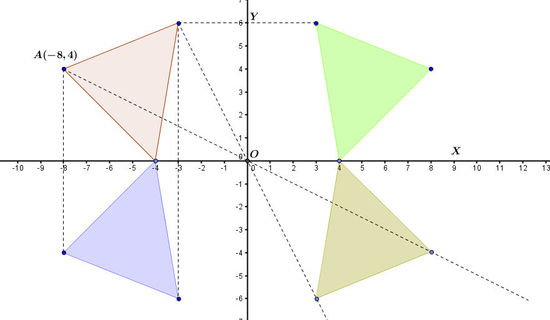
Narysuj Trojkat Symetryczny Do Trojkata T

Hej Studenci! Przygotujcie się na fascynującą podróż przez geometrię, gdzie nauczymy się rysować trójkąty symetryczne. To nie tylko kolejna lekcja, to brama do głębszego zrozumienia przestrzeni i transformacji. Bez obaw, rozłożymy to na czynniki pierwsze! Przejdźmy razem krok po kroku przez proces rysowania trójkąta symetrycznego do danego trójkąta T.

Czym jest Symetria?

Zanim zaczniemy rysować, musimy zrozumieć, co to w ogóle znaczy, że coś jest symetryczne. W geometrii, symetria (symetria osiowa) odnosi się do sytuacji, w której dana figura jest odbiciem lustrzanym innej figury względem pewnej prostej, zwanej osią symetrii. Wyobraź sobie, że masz rysunek i składasz go wzdłuż pewnej linii. Jeśli obie połówki idealnie się pokrywają, to figura jest symetryczna względem tej linii.

Oś Symetrii

Kluczowym elementem symetrii osiowej jest właśnie oś symetrii. Jest to prosta, względem której dokonuje się odbicie. Każdy punkt na jednej stronie osi ma swój odpowiednik na drugiej stronie, w dokładnie takiej samej odległości od osi, ale po przeciwnej stronie. Myśl o niej jak o lustrze! To przez nią patrzymy, aby zobaczyć odbity obraz.

Jak Narysować Trójkąt Symetryczny?

Ok, teoria za nami. Teraz przejdźmy do praktyki! Załóżmy, że mamy trójkąt T i chcemy narysować trójkąt T' (czytaj: T prim) symetryczny do T względem danej osi symetrii l. Oto krok po kroku, jak to zrobić:

1. Krok 1: Określ Oś Symetrii. Upewnij się, że masz jasno określoną oś symetrii (linię l). Może być narysowana na kartce, opisana słownie (np. "oś OX"), lub podana w równaniu (np. "y = 2"). Od tego, gdzie umieścisz oś, zależy wygląd symetrycznego trójkąta.
2. Krok 2: Znajdź Wierzchołki Trójkąta T. Zidentyfikuj wszystkie wierzchołki trójkąta T. Nazwijmy je A, B i C. Będziemy musieli znaleźć ich odpowiedniki po drugiej stronie osi symetrii.
3. Krok 3: Wyznacz Odległość od Osi Symetrii. Dla każdego wierzchołka (A, B, C), zmierz odległość od tego punktu do osi symetrii l. Pamiętaj, że odległość mierzymy po linii prostopadłej do osi l. To bardzo ważne! Musisz mierzyć prostopadle!
4. Krok 4: Znajdź Punkty Symetryczne. Dla każdego wierzchołka, znajdź punkt po drugiej stronie osi symetrii, w dokładnie tej samej odległości, co oryginalny wierzchołek. Zatem, jeśli punkt A był 3 cm od osi, to punkt A' (czytaj: A prim), jego odpowiednik, również będzie 3 cm od osi, ale po drugiej stronie. To właśnie będą wierzchołki naszego nowego trójkąta T': A', B' i C'.
5. Krok 5: Połącz Punkty. Połącz punkty A', B' i C', aby utworzyć trójkąt T'. Gratulacje! Właśnie narysowałeś trójkąt symetryczny do trójkąta T względem osi symetrii l.

Wskazówki i Triki

• Używaj Ekierki: Do mierzenia odległości i rysowania linii prostopadłych do osi symetrii, ekierka będzie twoim najlepszym przyjacielem. Zapewni Ci dokładność.
• Sprawdź Wynik: Upewnij się, że odległość każdego wierzchołka od osi jest taka sama, jak odległość jego odpowiednika. Sprawdź, czy "odbicie" wygląda logicznie.
• Zacznij od Prostych Przykładów: Zanim zaczniesz rozwiązywać skomplikowane zadania, poćwicz na prostych trójkątach i osiach symetrii (np. osi OX i OY).

Przykładowe Zadanie

Załóżmy, że mamy trójkąt o wierzchołkach A(1,1), B(3,1), C(2,3) i chcemy znaleźć trójkąt symetryczny względem osi OX (czyli linii y = 0).

1. Oś Symetrii: Oś OX (y = 0)
2. Wierzchołki: A(1,1), B(3,1), C(2,3)
3. Odległości od Osi OX:
   • A: Odległość = 1
   • B: Odległość = 1
   • C: Odległość = 3
4. Punkty Symetryczne:
   • A': (1,-1) (y-owa współrzędna zmienia znak)
   • B': (3,-1) (y-owa współrzędna zmienia znak)
   • C': (2,-3) (y-owa współrzędna zmienia znak)
5. Trójkąt Symetryczny: Trójkąt o wierzchołkach A'(1,-1), B'(3,-1), C'(2,-3).

Co Się Dzieje z Koordynatami?

To bardzo ważne spostrzeżenie! Jeśli odbijamy względem osi OX (y=0), to zmienia się znak współrzędnej y, a x zostaje bez zmian. Jeśli odbijamy względem osi OY (x=0), to zmienia się znak współrzędnej x, a y zostaje bez zmian. Jeśli odbijamy względem początku układu współrzędnych (0,0), to zmieniają się znaki obu współrzędnych! Warto to zapamiętać, bo bardzo ułatwia sprawę!

Podsumowanie

Nauczyliśmy się, jak narysować trójkąt symetryczny do danego trójkąta względem osi symetrii. Kluczowe kroki to:

• Zrozumienie definicji symetrii osiowej i roli osi symetrii.
• Znalezienie wierzchołków trójkąta.
• Zmierzanie odległości od każdego wierzchołka do osi symetrii (prostopadle!).
• Znalezienie punktów symetrycznych po drugiej stronie osi.
• Połączenie punktów, aby utworzyć trójkąt symetryczny.

Pamiętaj, ćwiczenie czyni mistrza! Im więcej będziesz ćwiczyć, tym łatwiej będzie Ci rysować trójkąty symetryczne. Powodzenia na egzaminie! Wierzę w Ciebie!