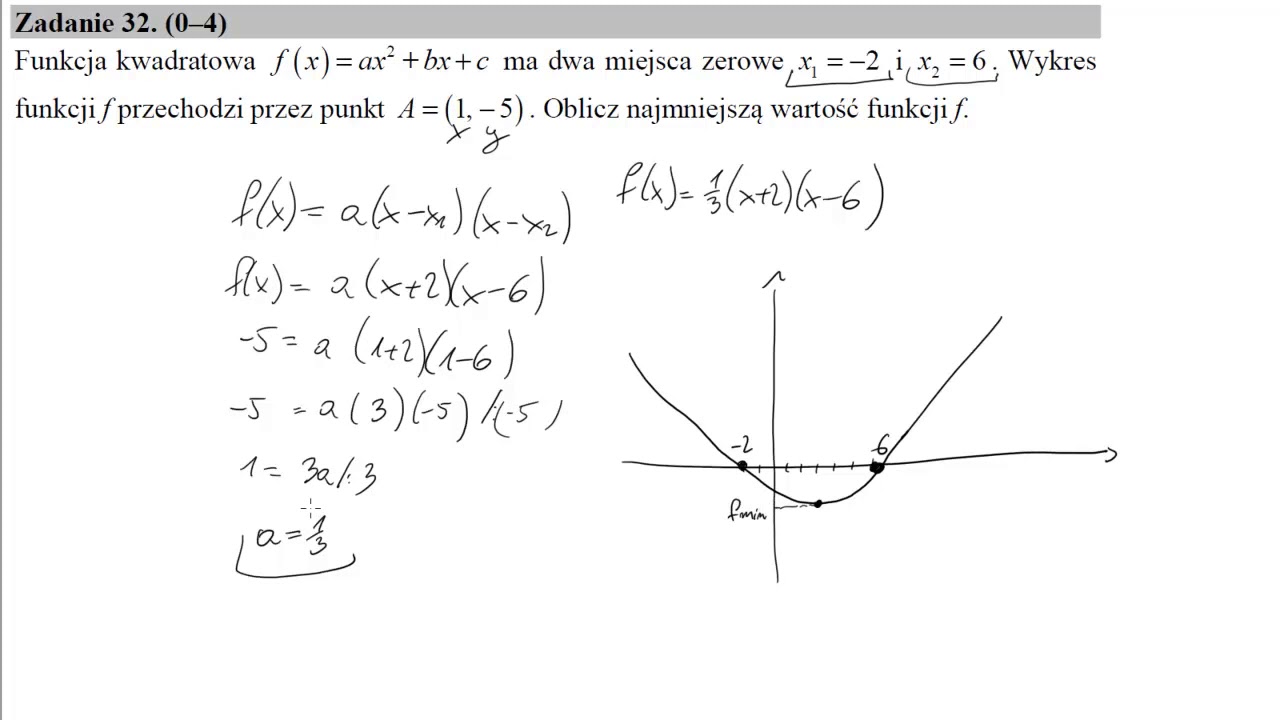
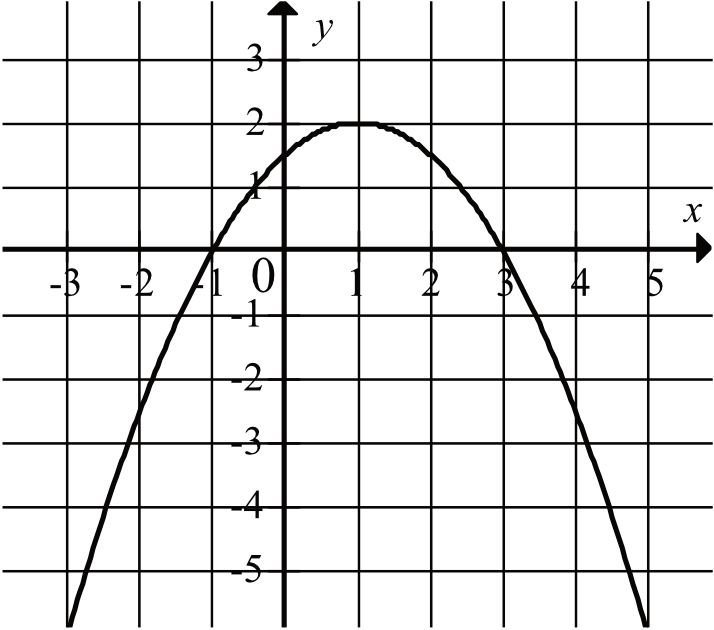
Napisz Wzór Funkcji Kwadratowej F Której Wykres Przedstawiono Na Rysunku

Dobrze, przejdźmy do tego od razu. Znalezienie wzoru funkcji kwadratowej, której wykres widzisz, to wbrew pozorom dość prosta sprawa. Istnieje kilka metod, a wybór zależy od tego, jakie informacje bezpośrednio odczytujesz z rysunku. Załóżmy, że dysponujesz dość czytelnym wykresem, z którego możesz wyciągnąć kilka kluczowych punktów.

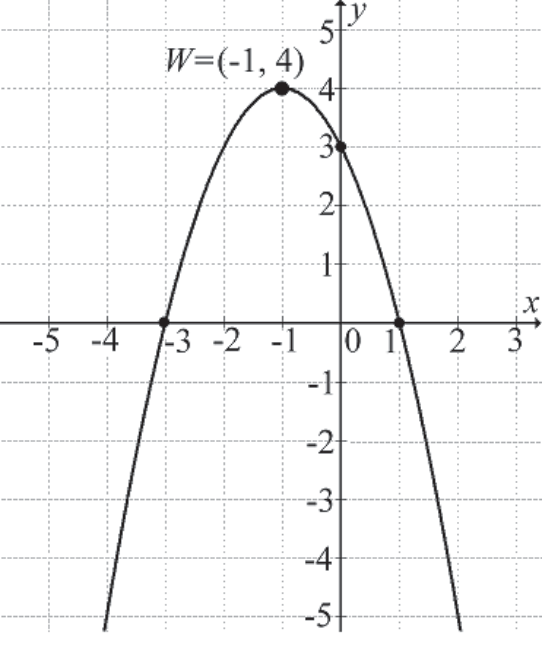
Sytuacja 1: Znamy wierzchołek i inny punkt na paraboli

Załóżmy, że z wykresu paraboli bez problemu odczytujesz współrzędne wierzchołka, powiedzmy W = (p, q). Pamiętaj, że postać kanoniczna funkcji kwadratowej wygląda następująco:

f(x) = a(x - p)² + q

Gdzie 'a' to współczynnik kierunkowy, który determinuje "rozciągnięcie" paraboli (jak bardzo jest "szeroka" lub "wąska") i czy ramiona są skierowane do góry (a > 0) czy do dołu (a < 0).

Skoro znasz (p, q), to masz już prawie wszystko! Potrzebujesz jeszcze wyznaczyć 'a'. W tym celu musisz odczytać z wykresu współrzędne innego punktu należącego do paraboli. Oznaczmy go jako P = (x₁, y₁). Podstawiasz te współrzędne do postaci kanonicznej:

y₁ = a(x₁ - p)² + q

I rozwiązujesz równanie ze względu na 'a'. Po wyznaczeniu 'a', podstawiasz jego wartość do postaci kanonicznej razem z wcześniej odczytanymi (p, q). To wszystko. Masz wzór funkcji w postaci kanonicznej. Jeśli potrzebujesz postać ogólną (f(x) = ax² + bx + c), po prostu wymnażasz i upraszczasz wyrażenie.

Na przykład: załóżmy, że W = (2, -1) oraz P = (0, 3). Wtedy:

3 = a(0 - 2)² + (-1) 3 = 4a - 1 4a = 4 a = 1

Wzór funkcji w postaci kanonicznej to: f(x) = (x - 2)² - 1. Przekształcając do postaci ogólnej:

f(x) = x² - 4x + 4 - 1 f(x) = x² - 4x + 3

Sytuacja 2: Znamy miejsca zerowe i inny punkt na paraboli

Jeśli z wykresu odczytujesz miejsca zerowe, czyli punkty przecięcia paraboli z osią OX (oznaczmy je jako x₁ i x₂), to możesz skorzystać z postaci iloczynowej funkcji kwadratowej:

f(x) = a(x - x₁)(x - x₂)

Podobnie jak wcześniej, potrzebujesz wyznaczyć współczynnik 'a'. W tym celu odczytujesz z wykresu współrzędne innego punktu P = (x₃, y₃), który należy do paraboli (ale nie jest miejscem zerowym!). Podstawiasz te współrzędne do postaci iloczynowej:

y₃ = a(x₃ - x₁)(x₃ - x₂)

Rozwiązujesz równanie ze względu na 'a', a następnie podstawiasz wyliczone 'a', x₁ i x₂ do wzoru w postaci iloczynowej. Gotowe! Jeśli chcesz postać ogólną, wymnażasz i upraszczasz.

Na przykład: załóżmy, że x₁ = -1, x₂ = 3 oraz P = (0, 6). Wtedy:

6 = a(0 - (-1))(0 - 3) 6 = a(1)(-3) 6 = -3a a = -2

Wzór funkcji w postaci iloczynowej to: f(x) = -2(x + 1)(x - 3). Przekształcając do postaci ogólnej:

f(x) = -2(x² - 3x + x - 3) f(x) = -2(x² - 2x - 3) f(x) = -2x² + 4x + 6

Sytuacja 3: Znamy trzy punkty na paraboli

Jeśli z wykresu możesz odczytać współrzędne trzech punktów należących do paraboli, powiedzmy P₁ = (x₁, y₁), P₂ = (x₂, y₂) i P₃ = (x₃, y₃), to możesz zapisać układ trzech równań z trzema niewiadomymi (a, b, c) w postaci ogólnej funkcji kwadratowej:

f(x) = ax² + bx + c

Układ równań wygląda następująco:

y₁ = ax₁² + bx₁ + c y₂ = ax₂² + bx₂ + c y₃ = ax₃² + bx₃ + c

Rozwiązujesz ten układ równań (np. metodą podstawiania, eliminacji Gaussa, używając macierzy itp.). Otrzymujesz wartości a, b i c, które podstawiasz do postaci ogólnej funkcji kwadratowej.

Na przykład: Załóżmy, że P₁ = (1, 2), P₂ = (2, 5), P₃ = (3, 10). Wtedy układ równań to:

2 = a(1)² + b(1) + c => a + b + c = 2 5 = a(2)² + b(2) + c => 4a + 2b + c = 5 10 = a(3)² + b(3) + c => 9a + 3b + c = 10

Rozwiązanie tego układu równań (pomijam tutaj kroki pośrednie, bo to już czysta algebra) daje: a = 1, b = 0, c = 1. Zatem wzór funkcji w postaci ogólnej to: f(x) = x² + 1.

Dodatkowe uwagi:

Pamiętaj, że dokładność uzyskanego wzoru zależy od dokładności odczytanych z wykresu współrzędnych punktów. Im dokładniej odczytasz te współrzędne, tym dokładniejszy będzie wzór funkcji. Czasami wykres jest na tyle niewyraźny, że odczytanie dokładnych współrzędnych jest niemożliwe i trzeba się posiłkować przybliżeniami.

Wybór metody zależy od tego, co najłatwiej odczytać z wykresu. Jeśli widać wierzchołek i jakiś inny punkt, najprościej użyć postaci kanonicznej. Jeśli widać miejsca zerowe i inny punkt, najprościej użyć postaci iloczynowej. Jeśli widzisz trzy dowolne punkty, to najprościej zapisać układ równań.

Zawsze warto sprawdzić, czy otrzymany wzór pasuje do wykresu. Możesz podstawić współrzędne kilku punktów odczytanych z wykresu do otrzymanego wzoru i sprawdzić, czy wyniki są zbliżone do wartości na wykresie. To pomoże ci wychwycić ewentualne błędy w obliczeniach lub niedokładności w odczytywaniu współrzędnych z wykresu.

Jeśli masz dostęp do oprogramowania graficznego (np. GeoGebra), możesz narysować wykres otrzymanej funkcji i porównać go z danym wykresem. To najbardziej wizualny i bezpośredni sposób na sprawdzenie poprawności rozwiązania. Pamiętaj, że niektóre programy mogą wymagać wprowadzenia wzoru w odpowiedniej składni.

Jeśli napotkasz trudności w rozwiązaniu układu równań, możesz skorzystać z kalkulatora macierzowego online lub oprogramowania do obliczeń symbolicznych (np. Wolfram Mathematica). Takie narzędzia mogą pomóc ci w szybkim i precyzyjnym rozwiązaniu układu równań.

Ważne jest, aby rozumieć związek między współczynnikami a, b, c we wzorze funkcji kwadratowej a kształtem paraboli. Współczynnik 'a' wpływa na kierunek ramion paraboli (do góry, jeśli a > 0, do dołu, jeśli a < 0) oraz na jej "rozciągnięcie". Współrzędne wierzchołka zależą od współczynników a, b, c (p = -b/2a, q = -Δ/4a). Miejsca zerowe zależą od współczynników a, b, c (x₁, x₂ = (-b ± √Δ) / 2a). Zrozumienie tych zależności ułatwia analizę wykresu i weryfikację otrzymanego wzoru.

I to w zasadzie wszystko. Praktyka czyni mistrza, więc spróbuj rozwiązać kilka przykładów i po pewnym czasie znajdowanie wzorów funkcji kwadratowych na podstawie wykresów stanie się dla ciebie intuicyjne.