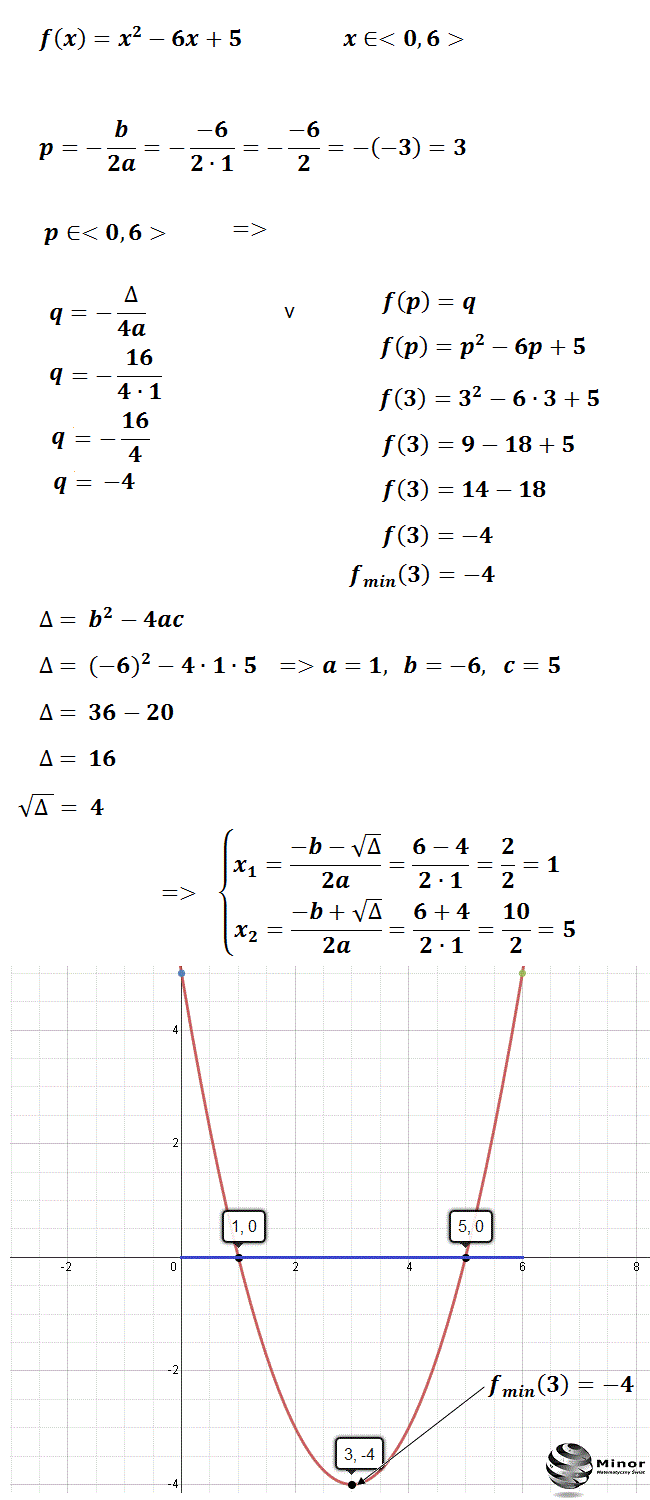Największą I Najmniejszą Wartość Funkcji Kwadratowej Bez Przedziału

Dobrze, oto artykuł odpowiadający na pytanie o znajdowanie największej i najmniejszej wartości funkcji kwadratowej bez przedziału, napisany zgodnie z Twoimi wytycznymi:

Funkcja kwadratowa, opisana ogólnym wzorem f(x) = ax² + bx + c, gdzie a, b i c są stałymi współczynnikami i a ≠ 0, charakteryzuje się parabolicznym wykresem. Zrozumienie, jak odnaleźć jej największą lub najmniejszą wartość, jest fundamentalne w wielu dziedzinach matematyki i jej zastosowaniach. Istotą jest analiza współczynnika 'a' oraz obliczenie współrzędnych wierzchołka paraboli.

Jeżeli współczynnik 'a' jest dodatni (a > 0), parabola skierowana jest ramionami do góry. Oznacza to, że funkcja osiąga minimum w swoim wierzchołku. Wartość minimalna to rzędna wierzchołka. Nie istnieje wartość maksymalna, ponieważ funkcja rośnie nieograniczenie w kierunku dodatnim, gdy x dąży do plus lub minus nieskończoności.

Z kolei, jeżeli współczynnik 'a' jest ujemny (a < 0), parabola skierowana jest ramionami do dołu. W tym przypadku funkcja osiąga maksimum w swoim wierzchołku. Wartość maksymalna to rzędna wierzchołka. Nie istnieje wartość minimalna, ponieważ funkcja maleje nieograniczenie w kierunku ujemnym, gdy x dąży do plus lub minus nieskończoności.

Aby precyzyjnie określić współrzędne wierzchołka paraboli, wykorzystujemy wzory:

• x_w = -b / 2a (odcięta wierzchołka)
• y_w = f(x_w) = a(x_w)² + b(x_w) + c (rzędna wierzchołka, czyli wartość funkcji w punkcie x_w)

Alternatywnie, rzędną wierzchołka można obliczyć korzystając ze wzoru:

• y_w = -Δ / 4a, gdzie Δ (delta) = b² - 4ac jest wyróżnikiem trójmianu kwadratowego.

Obliczanie wyróżnika (Δ) jest kluczowe, ponieważ informuje nas o liczbie miejsc zerowych funkcji kwadratowej. Jednak w kontekście znajdowania ekstremum funkcji (maksimum lub minimum) interesuje nas przede wszystkim do obliczenia współrzędnej y wierzchołka.

Przykłady Obliczania Wartości Ekstremalnych

Rozważmy kilka przykładów, aby utrwalić proces znajdowania wartości największej lub najmniejszej funkcji kwadratowej:

1. f(x) = 2x² - 8x + 6

   • Współczynnik a = 2 (dodatni), więc funkcja ma minimum.
   • x_w = -(-8) / (2 * 2) = 8 / 4 = 2
   • y_w = f(2) = 2(2)² - 8(2) + 6 = 8 - 16 + 6 = -2

   Funkcja f(x) osiąga minimum równe -2 w punkcie x = 2. Nie ma wartości maksymalnej.

2. g(x) = -x² + 4x - 5

   • Współczynnik a = -1 (ujemny), więc funkcja ma maksimum.
   • x_w = -4 / (2 * -1) = -4 / -2 = 2
   • y_w = g(2) = -(2)² + 4(2) - 5 = -4 + 8 - 5 = -1

   Funkcja g(x) osiąga maksimum równe -1 w punkcie x = 2. Nie ma wartości minimalnej.

3. h(x) = x² + 6x + 9

   • Współczynnik a = 1 (dodatni), więc funkcja ma minimum.
   • x_w = -6 / (2 * 1) = -6 / 2 = -3
   • y_w = h(-3) = (-3)² + 6(-3) + 9 = 9 - 18 + 9 = 0

   Funkcja h(x) osiąga minimum równe 0 w punkcie x = -3. Nie ma wartości maksymalnej. Zauważmy, że delta w tym przypadku wynosi 0 (Δ = 6² - 4 * 1 * 9 = 36 - 36 = 0), co oznacza, że wierzchołek paraboli leży na osi x.

4. k(x) = -2x² - 4x + 3

   • Współczynnik a = -2 (ujemny), więc funkcja ma maksimum.
   • x_w = -(-4) / (2 * -2) = 4 / -4 = -1
   • y_w = k(-1) = -2(-1)² - 4(-1) + 3 = -2 + 4 + 3 = 5

   Funkcja k(x) osiąga maksimum równe 5 w punkcie x = -1. Nie ma wartości minimalnej.

5. l(x) = 0.5x² - 3x + 1

   • Współczynnik a = 0.5 (dodatni), więc funkcja ma minimum.
   • x_w = -(-3) / (2 * 0.5) = 3 / 1 = 3
   • y_w = l(3) = 0.5(3)² - 3(3) + 1 = 4.5 - 9 + 1 = -3.5

   Funkcja l(x) osiąga minimum równe -3.5 w punkcie x = 3. Nie ma wartości maksymalnej.

Ważne jest, aby pamiętać o interpretacji wyników. Zawsze należy sprawdzić znak współczynnika 'a', aby określić, czy funkcja ma minimum, czy maksimum. Następnie, obliczając współrzędne wierzchołka, znajdujemy punkt, w którym to ekstremum występuje, oraz wartość tego ekstremum.

Zastosowanie w Zadaniach Optymalizacyjnych

Znajdowanie największej lub najmniejszej wartości funkcji kwadratowej ma szerokie zastosowanie w problemach optymalizacyjnych. Przykładowo, możemy chcieć znaleźć wymiary prostokąta o danym obwodzie, który ma największe pole, lub ustalić, przy jakiej cenie produktu zysk firmy będzie maksymalny. W takich przypadkach często udaje się sformułować funkcję kwadratową opisującą dany problem, a następnie znaleźć jej wierzchołek, który odpowiada rozwiązaniu optymalnemu.

Przykładowo, rozważmy problem: chcemy zbudować wybieg dla zwierząt w kształcie prostokąta, mając do dyspozycji 100 metrów siatki. Jakie wymiary powinien mieć ten prostokąt, aby jego pole było największe?

Oznaczmy długość jednego z boków prostokąta jako x. Wtedy długość drugiego boku wynosi (100 - 2x) / 2 = 50 - x. Pole prostokąta, P, wyraża się wzorem:

P(x) = x(50 - x) = 50x - x²

Jest to funkcja kwadratowa z a = -1 (ujemny), więc ma maksimum. Obliczamy x_w:

x_w = -50 / (2 * -1) = 25

Zatem, jeden bok prostokąta powinien mieć długość 25 metrów, a drugi:

50 - x_w = 50 - 25 = 25 metrów.

Największe pole wybiegu uzyskamy, gdy będzie on kwadratem o boku 25 metrów. Pole to wynosi 25 * 25 = 625 metrów kwadratowych.

Podsumowując, umiejętność znajdowania największej i najmniejszej wartości funkcji kwadratowej bez ograniczeń przedziału jest kluczowa dla rozwiązywania problemów optymalizacyjnych i zrozumienia zachowania się funkcji kwadratowych w ogólności. Analiza współczynnika 'a' oraz poprawne obliczenie współrzędnych wierzchołka paraboli to podstawowe kroki w tym procesie. Należy pamiętać o właściwej interpretacji wyników w kontekście danego problemu.