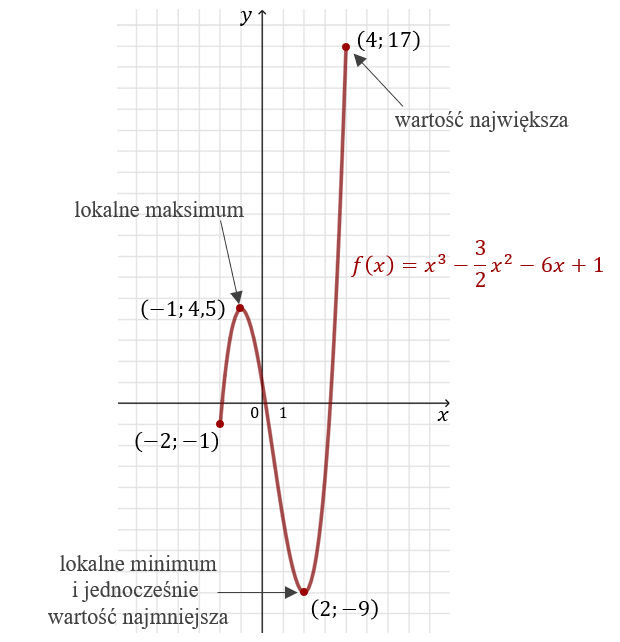
Najmniejsza Lub Największą Wartość Funkcji W Jakimś Przedziale

Zaczynamy podróż po świecie funkcji, by znaleźć ich ekstrema – największe i najmniejsze wartości w określonych granicach. Odkryjemy metody, które pozwolą nam zlokalizować te kluczowe punkty na wykresie, wykorzystując narzędzia analizy matematycznej. Bez zbędnych wstępów, przejdźmy do konkretów!

Na samym początku musimy zdefiniować przedział, na którym szukamy ekstremów. Może to być przedział domknięty (np. [a, b]), otwarty (np. (a, b)) lub półotwarty (np. [a, b) lub (a, b]). Wybór przedziału ma kluczowe znaczenie, ponieważ wpływa na to, czy funkcja osiąga swoje ekstrema w jego granicach.

Pierwszym krokiem jest wyznaczenie punktów krytycznych funkcji w danym przedziale. Są to punkty, w których pochodna funkcji jest równa zero lub nie istnieje. Pochodna funkcji informuje nas o tempie zmiany funkcji w danym punkcie. Gdy pochodna jest równa zero, funkcja przestaje rosnąć lub maleć – potencjalne miejsce wystąpienia ekstremum.

Obliczamy pochodną funkcji f(x), oznaczaną jako f'(x). Następnie szukamy rozwiązań równania f'(x) = 0. Te rozwiązania to potencjalne punkty ekstremalne. Dodatkowo, musimy sprawdzić, czy pochodna funkcji istnieje w każdym punkcie przedziału. Jeśli istnieją punkty, w których pochodna nie istnieje (np. punkty ostre, załamania wykresu), również je uwzględniamy jako potencjalne punkty ekstremalne.

Po wyznaczeniu punktów krytycznych, oceniamy, czy leżą one wewnątrz zadanego przedziału. Punkty krytyczne leżące poza przedziałem nie są dla nas interesujące w kontekście poszukiwania ekstremów w tym konkretnym przedziale.

Kolejny etap to obliczenie wartości funkcji w punktach krytycznych, które należą do przedziału. Obliczamy również wartości funkcji na krańcach przedziału, jeśli jest to przedział domknięty lub półotwarty.

Spośród wszystkich obliczonych wartości funkcji, wybieramy największą i najmniejszą. Największa wartość to maksimum funkcji w danym przedziale, a najmniejsza wartość to minimum funkcji w tym przedziale.

Analiza Drugiej Pochodnej

Alternatywną metodą identyfikacji ekstremów jest analiza drugiej pochodnej. Po wyznaczeniu punktów krytycznych, obliczamy drugą pochodną funkcji f''(x). Następnie podstawiamy do niej wartości punktów krytycznych.

Jeśli f''(x) > 0 w punkcie krytycznym, to funkcja osiąga w tym punkcie minimum lokalne. Wykres funkcji jest w tym miejscu wypukły w dół.

Jeśli f''(x) < 0 w punkcie krytycznym, to funkcja osiąga w tym punkcie maksimum lokalne. Wykres funkcji jest w tym miejscu wypukły w górę.

Jeśli f''(x) = 0, test drugiej pochodnej jest nierozstrzygający i nie możemy jednoznacznie określić, czy w danym punkcie występuje ekstremum. W takim przypadku musimy posłużyć się innymi metodami, np. analizą znaku pierwszej pochodnej w otoczeniu punktu krytycznego.

Analizując znak pierwszej pochodnej, możemy określić, czy funkcja rośnie czy maleje w otoczeniu punktu krytycznego. Jeśli funkcja rośnie po lewej stronie punktu krytycznego i maleje po prawej, to w tym punkcie występuje maksimum lokalne. Jeśli funkcja maleje po lewej stronie punktu krytycznego i rośnie po prawej, to w tym punkcie występuje minimum lokalne.

Rozważmy przykład. Niech f(x) = x^3 - 3x^2 + 2, a przedział to [-1, 3].

Obliczamy pierwszą pochodną: f'(x) = 3x^2 - 6x.

Przyrównujemy pochodną do zera: 3x^2 - 6x = 0.

Wyciągamy 3x przed nawias: 3x(x - 2) = 0.

Otrzymujemy dwa punkty krytyczne: x = 0 oraz x = 2. Oba punkty leżą w przedziale [-1, 3].

Obliczamy drugą pochodną: f''(x) = 6x - 6.

Sprawdzamy znak drugiej pochodnej w punktach krytycznych:

• f''(0) = 6(0) - 6 = -6 < 0, więc w punkcie x = 0 występuje maksimum lokalne.

• f''(2) = 6(2) - 6 = 6 > 0, więc w punkcie x = 2 występuje minimum lokalne.

Obliczamy wartości funkcji w punktach krytycznych i na krańcach przedziału:

• f(-1) = (-1)^3 - 3(-1)^2 + 2 = -1 - 3 + 2 = -2

• f(0) = (0)^3 - 3(0)^2 + 2 = 2

• f(2) = (2)^3 - 3(2)^2 + 2 = 8 - 12 + 2 = -2

• f(3) = (3)^3 - 3(3)^2 + 2 = 27 - 27 + 2 = 2

Porównujemy wartości funkcji: -2, 2, -2, 2.

Największa wartość funkcji w przedziale [-1, 3] to 2, a najmniejsza wartość to -2.

Warto pamiętać, że znalezienie ekstremów funkcji w przedziale ma wiele zastosowań w różnych dziedzinach nauki i techniki. Na przykład, w ekonomii możemy szukać maksymalnego zysku lub minimalnych kosztów. W fizyce możemy szukać punktu równowagi lub minimalnej energii. W inżynierii możemy optymalizować parametry konstrukcji, aby uzyskać maksymalną wytrzymałość lub minimalną wagę.

Analiza monotoniczności funkcji, czyli sprawdzanie, czy funkcja rośnie, czy maleje, jest ściśle powiązana z poszukiwaniem ekstremów. Wykorzystując znak pierwszej pochodnej, możemy określić, w jakich przedziałach funkcja rośnie, a w jakich maleje. Informacje te są cenne przy szkicowaniu wykresu funkcji i identyfikacji ekstremów.

Uwagi Końcowe

Poszukiwanie największej i najmniejszej wartości funkcji w danym przedziale jest ważnym zagadnieniem w analizie matematycznej. Prezentowane metody, oparte na analizie pochodnych, pozwalają na efektywne zlokalizowanie ekstremów funkcji. Pamiętajmy o dokładnym określeniu przedziału, wyznaczeniu punktów krytycznych i analizie wartości funkcji w tych punktach oraz na krańcach przedziału. Analiza drugiej pochodnej może pomóc w identyfikacji rodzaju ekstremum (maksimum lub minimum). W przypadku wątpliwości, warto przeanalizować znak pierwszej pochodnej w otoczeniu punktu krytycznego. Zastosowanie tych technik pozwala na rozwiązywanie problemów optymalizacyjnych w różnych dziedzinach.