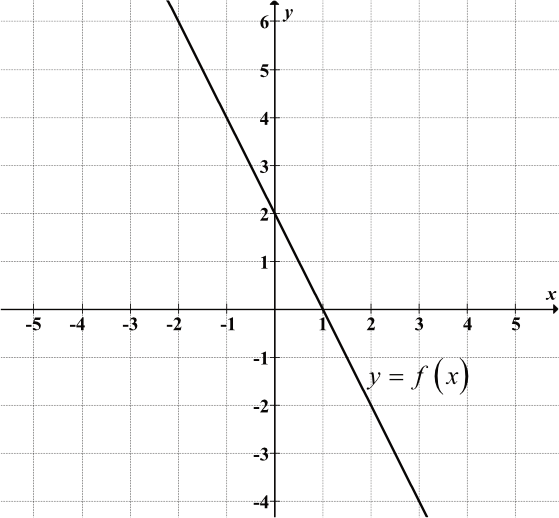Na Rysunku Przedstawiony Jest Fragment Wykresu Funkcji Liniowej F

Dobra, przyjrzyjmy się temu fragmentowi wykresu funkcji liniowej f. Zazwyczaj, gdy widzimy taki fragment, pytania dotyczą kilku podstawowych rzeczy: wzoru funkcji, miejsca zerowego, punktu przecięcia z osią Y, czy funkcja jest rosnąca, malejąca, czy stała, no i oczywiście, wartości funkcji dla konkretnych argumentów.

Zacznijmy od samego początku - funkcja liniowa. To taka funkcja, której wykresem jest linia prosta. Jej ogólny wzór to f(x) = ax + b. Naszym zadaniem jest znalezienie wartości a i b na podstawie tego, co widzimy na wykresie.

Żeby wyznaczyć a i b, potrzebujemy dwóch punktów należących do tej prostej. Te punkty możemy odczytać bezpośrednio z wykresu. Zwróć uwagę, gdzie prosta przecina siatkę – te przecięcia z liniami pomocniczymi układu współrzędnych są najłatwiejsze do odczytania. Załóżmy, że widzimy dwa punkty: A = (x₁, y₁) i B = (x₂, y₂).

Teraz możemy obliczyć a, czyli współczynnik kierunkowy prostej. Wzór na a to: a = (y₂ - y₁) / (x₂ - x₁). Po prostu odejmujemy od siebie współrzędne y i dzielimy przez różnicę współrzędnych x. Ważne jest, żeby kolejność odejmowania była taka sama w liczniku i mianowniku! Jak już obliczymy a, mamy połowę sukcesu.

Teraz obliczamy b. Do tego wykorzystamy jeden z punktów, które już znamy (na przykład punkt A) i wzór funkcji: f(x) = ax + b. Podstawiamy do tego wzoru współrzędne punktu A (czyli x₁ i y₁) oraz wyliczone wcześniej a. Otrzymujemy równanie: y₁ = a * x₁ + b. Z tego równania wyliczamy b: b = y₁ - a * x₁.

Mając a i b, możemy zapisać pełny wzór funkcji liniowej f(x) = ax + b. To bardzo ważne, bo teraz możemy obliczyć wartość funkcji dla dowolnego x. Po prostu podstawiamy x do wzoru i obliczamy f(x).

Analiza Funkcji

Po znalezieniu wzoru funkcji, możemy przejść do analizy jej właściwości.

• Miejsce zerowe: To taki x, dla którego f(x) = 0. Czyli, szukamy punktu, w którym wykres funkcji przecina oś X. Żeby go znaleźć, rozwiązujemy równanie: ax + b = 0. Przekształcamy je i otrzymujemy: x = -b / a. Jeśli a jest równe zero, to funkcja jest stała i albo nie ma miejsc zerowych (jeśli b jest różne od zera), albo ma nieskończenie wiele miejsc zerowych (jeśli b jest równe zero).

• Punkt przecięcia z osią Y: To punkt, w którym wykres funkcji przecina oś Y. Ten punkt jest bardzo prosty do odczytania z wzoru funkcji. Jego współrzędne to (0, b). Czyli, po prostu patrzymy na wartość b we wzorze f(x) = ax + b.

• Monotoniczność funkcji: Mówi nam, czy funkcja jest rosnąca, malejąca, czy stała. O tym decyduje współczynnik a.

  • Jeśli a > 0, to funkcja jest rosnąca. Oznacza to, że wraz ze wzrostem x, rośnie również f(x).
  • Jeśli a < 0, to funkcja jest malejąca. Oznacza to, że wraz ze wzrostem x, maleje f(x).
  • Jeśli a = 0, to funkcja jest stała. Oznacza to, że f(x) ma zawsze tę samą wartość, niezależnie od x. Wykres takiej funkcji to linia pozioma.

• Wartość funkcji dla danego argumentu: Jeśli chcemy obliczyć wartość funkcji dla jakiegoś konkretnego x, na przykład x = 5, to po prostu podstawiamy 5 do wzoru funkcji f(x) = ax + b. Czyli, obliczamy f(5) = a * 5 + b. Wynik tego obliczenia to wartość funkcji dla x = 5.

Przykładowe Zadanie:

Załóżmy, że z wykresu odczytaliśmy dwa punkty: A = (1, 2) i B = (3, 6).

1. Obliczamy a: a = (6 - 2) / (3 - 1) = 4 / 2 = 2.
2. Obliczamy b: Wykorzystujemy punkt A = (1, 2): 2 = 2 * 1 + b. Zatem, b = 2 - 2 = 0.
3. Wzór funkcji: f(x) = 2x + 0, czyli f(x) = 2x.
4. Miejsce zerowe: 2x = 0, zatem x = 0.
5. Punkt przecięcia z osią Y: (0, 0).
6. Monotoniczność: a = 2 > 0, więc funkcja jest rosnąca.
7. Wartość funkcji dla x = 4: f(4) = 2 * 4 = 8.

Dodatkowe Wskazówki:

• Upewnij się, że dokładnie odczytujesz współrzędne punktów z wykresu. Błąd w odczycie może prowadzić do błędnych obliczeń.
• Sprawdzaj swoje obliczenia, żeby uniknąć błędów arytmetycznych.
• Jeśli masz wątpliwości, narysuj wykres funkcji, którą obliczyłeś, i porównaj go z oryginalnym wykresem. To pomoże Ci sprawdzić, czy Twoje obliczenia są poprawne.
• Pamiętaj, że funkcja liniowa jest bardzo prostą funkcją i jej analiza nie powinna sprawiać większych problemów.

Podsumowanie:

Praca z fragmentem wykresu funkcji liniowej sprowadza się do znalezienia wzoru tej funkcji, a następnie do analizy jej właściwości. Znalezienie wzoru wymaga odczytania współrzędnych dwóch punktów z wykresu i obliczenia współczynników a i b. Następnie możemy obliczyć miejsce zerowe, punkt przecięcia z osią Y, określić monotoniczność funkcji i obliczyć wartość funkcji dla dowolnego argumentu. Pamiętaj o dokładności odczytu i sprawdzaniu obliczeń! Powodzenia!