Na Rysunku Przedstawiono Wykres Jednej Z Podanych Funkcji Której

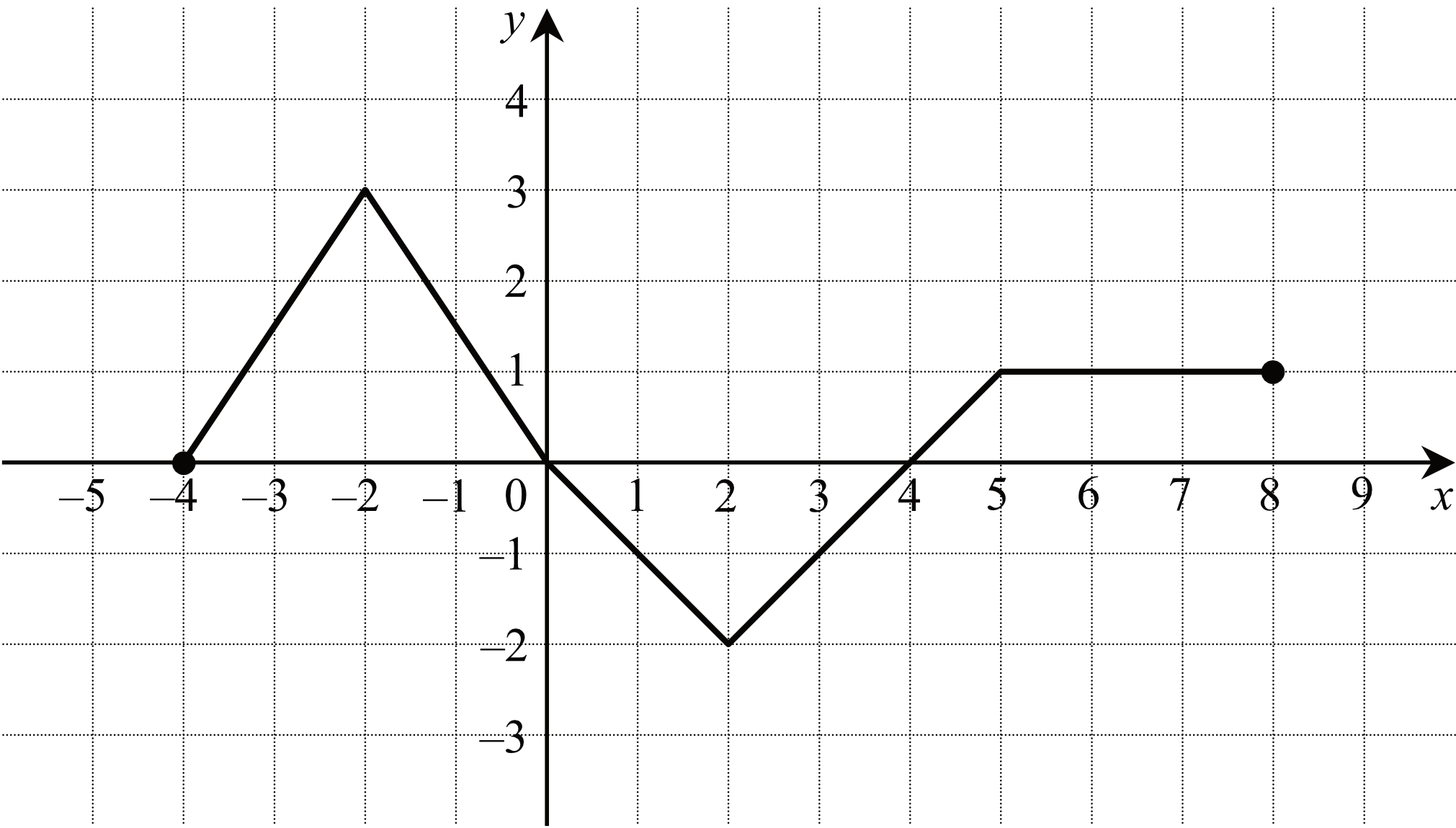
Okej, spróbujmy to wyjaśnić tak, żeby każdy zrozumiał, bez wchodzenia w zbyt skomplikowane szczegóły. Często spotykamy się z zadaniem, gdzie widzimy wykres jakiejś funkcji i musimy odgadnąć, która to funkcja. To może wydawać się trudne, ale z kilkoma wskazówkami staje się znacznie prostsze.

Najpierw spójrzmy na kształt wykresu. Kształt jest bardzo ważny, ponieważ każda podstawowa funkcja (liniowa, kwadratowa, wykładnicza, trygonometryczna) ma swój charakterystyczny wygląd.

• Linia prosta: To najprostsze. Jeśli widzisz prostą linię, to masz do czynienia z funkcją liniową. Ogólny wzór takiej funkcji to y = ax + b, gdzie 'a' to współczynnik kierunkowy (mówi nam, czy linia idzie w górę, czy w dół), a 'b' to punkt przecięcia z osią Y.
• Parabola: To taka litera "U" albo "odwrócone U". Parabola oznacza, że masz do czynienia z funkcją kwadratową. Jej ogólny wzór to y = ax² + bx + c. Kierunek paraboli (do góry czy do dołu) zależy od znaku 'a'.
• Krzywa wykładnicza: Charakteryzuje się tym, że rośnie bardzo szybko (albo maleje bardzo szybko). Funkcja wykładnicza ma wzór y = aˣ, gdzie 'a' jest liczbą większą od 0 i różną od 1.
• Funkcje trygonometryczne (sinus, cosinus): Wyglądają jak fale. Mają powtarzający się wzór. Sinus zaczyna się w punkcie (0, 0), a cosinus w punkcie (0, 1).

Jak analizować wykres?

Spójrzmy na kilka konkretnych punktów i cech wykresu, które pomogą nam dopasować go do odpowiedniej funkcji.

1. Punkty przecięcia z osiami: Zobacz, gdzie wykres przecina oś X (oś poziomą) i oś Y (oś pionową). Te punkty dają nam ważne informacje. Punkt przecięcia z osią Y odczytujemy bezpośrednio z wykresu. Dla funkcji liniowej, jest to wartość 'b' we wzorze y = ax + b. Punkty przecięcia z osią X to miejsca, gdzie funkcja ma wartość zero, czyli są to tak zwane miejsca zerowe.
2. Ekstrema (maksima i minima): Sprawdź, czy wykres ma jakieś "górki" (maksima) lub "dołki" (minima). Funkcje kwadratowe mają jedno ekstremum (wierzchołek paraboli). Funkcje trygonometryczne mają ich nieskończenie wiele.
3. Symetria: Zobacz, czy wykres jest symetryczny względem jakiejś osi. Parabola jest symetryczna względem prostej przechodzącej przez jej wierzchołek.
4. Asymptoty: To proste, do których wykres zbliża się bardzo blisko, ale nigdy ich nie przecina. Funkcje wykładnicze i hiperbole często mają asymptoty.
5. Monotoniczność: Zbadaj, czy funkcja rośnie, maleje, czy jest stała na poszczególnych przedziałach. Funkcja rosnąca idzie w górę, patrząc od lewej do prawej. Funkcja malejąca idzie w dół.

Teraz, mając te narzędzia, możemy krok po kroku eliminować możliwe opcje.

Przykład:

Załóżmy, że widzisz wykres, który wygląda jak parabola skierowana ramionami do góry. To od razu mówi nam, że mamy do czynienia z funkcją kwadratową (y = ax² + bx + c), gdzie 'a' jest dodatnie. Sprawdźmy, gdzie parabola przecina oś Y. Powiedzmy, że przecina ją w punkcie (0, 2). To oznacza, że 'c' we wzorze funkcji kwadratowej wynosi 2. Teraz spójrz na miejsca zerowe (punkty przecięcia z osią X). Powiedzmy, że są to punkty (-1, 0) i (3, 0). Mając te informacje, możemy spróbować znaleźć wzór konkretnej funkcji. Możemy podstawić te punkty do wzoru ogólnego i rozwiązać układ równań, aby znaleźć wartości 'a' i 'b'. Albo, alternatywnie, możemy skorzystać z postaci iloczynowej funkcji kwadratowej: y = a(x - x₁)(x - x₂), gdzie x₁ i x₂ to miejsca zerowe. W naszym przypadku: y = a(x + 1)(x - 3). Wiemy, że w punkcie x = 0, y = 2, więc możemy to podstawić: 2 = a(0 + 1)(0 - 3), czyli 2 = -3a. Stąd a = -2/3. Ostatecznie wzór funkcji to: y = (-2/3)(x + 1)(x - 3).

Inny przykład:

Wyobraźmy sobie wykres, który wygląda jak linia prosta idąca w górę od lewej do prawej. Oznacza to, że mamy do czynienia z funkcją liniową (y = ax + b), gdzie 'a' jest dodatnie. Jeśli linia przecina oś Y w punkcie (0, -1), to 'b' wynosi -1. Jeśli wiemy, że linia przechodzi przez punkt (1, 2), to możemy to podstawić do wzoru: 2 = a * 1 - 1, czyli 2 = a - 1. Stąd a = 3. Ostatecznie wzór funkcji to: y = 3x - 1.

Kiedy mam problem z zadaniem?

Jeśli masz kilka funkcji do wyboru, a wykres wygląda skomplikowanie, spróbuj podstawiać kilka wartości x do każdej funkcji i sprawdzić, czy otrzymane wartości y zgadzają się z tym, co widzisz na wykresie. To często pomaga wyeliminować błędne odpowiedzi. Na przykład, jeśli widzisz, że dla x = 0, y = 5, to od razu możesz wykluczyć wszystkie funkcje, które dla x = 0 dają inną wartość.

Pamiętaj, że najważniejsze to spokojnie przeanalizować wykres, zidentyfikować jego kluczowe cechy i porównać je z charakterystycznymi cechami podstawowych funkcji. Ćwiczenie czyni mistrza! Im więcej zadań rozwiążesz, tym łatwiej będzie Ci rozpoznawać różne typy funkcji na podstawie ich wykresów.

Jeśli dostaniesz zadanie z bardziej złożoną funkcją, na przykład z przesuniętą lub rozciągniętą funkcją trygonometryczną, proces analizy jest podobny. Skup się na ustaleniu, jaka jest podstawowa funkcja (sinus, cosinus), a następnie spróbuj zidentyfikować parametry, które wpłynęły na jej kształt (amplituda, okres, przesunięcie).

Na przykład, funkcja y = 2sin(x) ma amplitudę równą 2, co oznacza, że jej wartości wahają się między -2 a 2. Funkcja y = sin(2x) ma okres równy π, co oznacza, że pełny cykl fali powtarza się co π jednostek. Funkcja y = sin(x + π/2) jest przesunięta w lewo o π/2 jednostki względem standardowej funkcji sinus.

Podsumowując, rozpoznawanie funkcji na podstawie wykresu to umiejętność, którą można nabyć poprzez systematyczną analizę i ćwiczenia. Skup się na kształcie wykresu, punktach przecięcia z osiami, ekstremach, symetrii i asymptotach. Pamiętaj, że każda funkcja ma swój charakterystyczny wygląd, który można zidentyfikować, analizując jej wzór i właściwości.