Na Rysunku Przedstawiono Szesciokat Foremny O Boku Rownym 2

Na rysunku przedstawiono sześciokąt foremny o boku równym 2. Zastanówmy się, jakie informacje możemy wyciągnąć z tego faktu i jak możemy wykorzystać tę wiedzę do obliczeń związanych z tym sześciokątem.

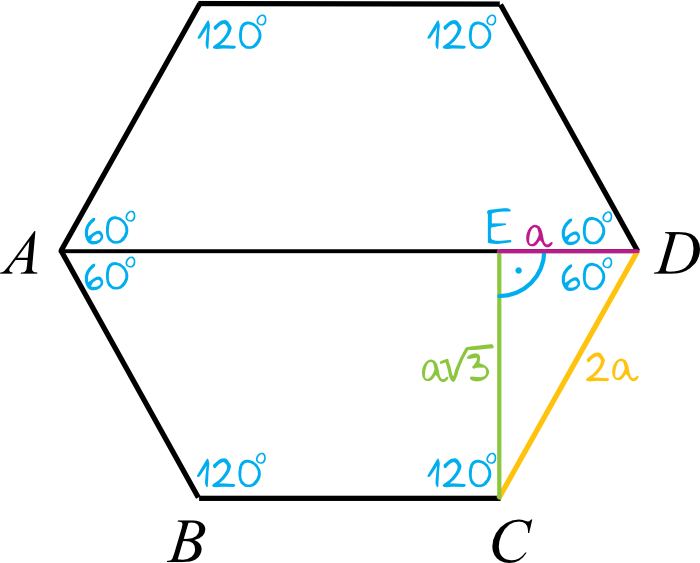
Sześciokąt foremny to figura geometryczna, która posiada sześć równych boków i sześć równych kątów wewnętrznych. Każdy kąt wewnętrzny sześciokąta foremnego ma miarę 120 stopni. Jest to konsekwencja wzoru na sumę kątów wewnętrznych wielokąta, która wynosi (n-2) * 180 stopni, gdzie n to liczba boków. W przypadku sześciokąta (6-2) * 180 = 4 * 180 = 720 stopni. Dzieląc tę wartość przez 6 (liczbę kątów), otrzymujemy 120 stopni.

Skoro wiemy, że bok sześciokąta foremnego ma długość 2, możemy obliczyć jego obwód. Obwód to suma długości wszystkich boków. W przypadku sześciokąta foremnego o boku 2, obwód wynosi 6 * 2 = 12.

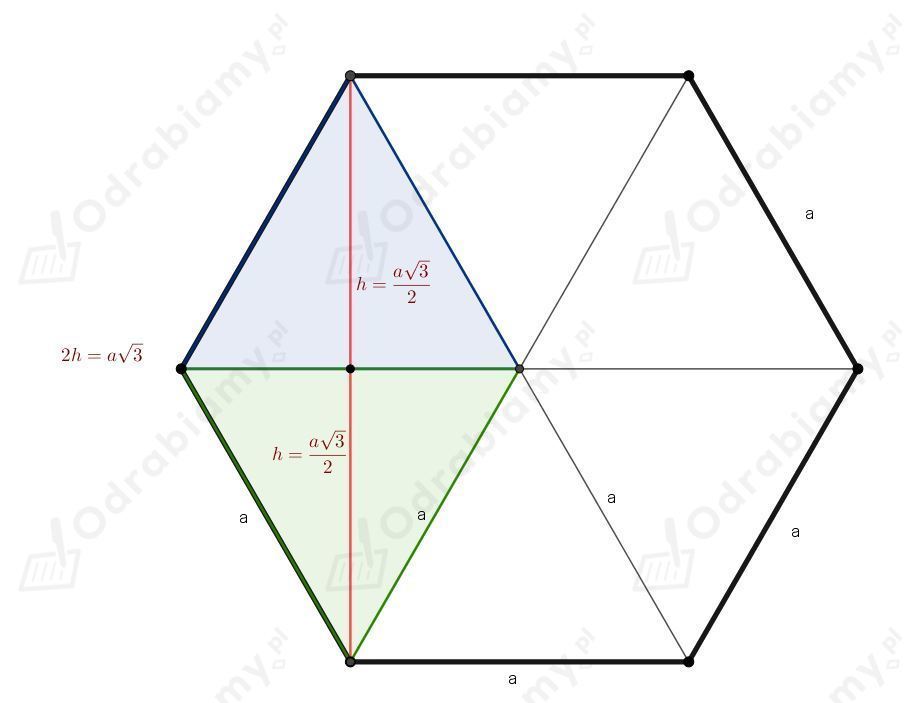
Możemy również przyjrzeć się diagonalom sześciokąta foremnego. Istnieją dwa rodzaje diagonali: krótsze i dłuższe. Dłuższe diagonale przechodzą przez środek sześciokąta i łączą przeciwległe wierzchołki. Krótsze diagonale łączą wierzchołki oddalone o dwa boki. Dłuższa diagonala ma długość dwa razy większą niż długość boku, czyli w naszym przypadku 2 * 2 = 4. Wynika to z faktu, że sześciokąt foremny można podzielić na sześć trójkątów równobocznych o boku równym długości boku sześciokąta. Dłuższa diagonala odpowiada dwóm bokom takiego trójkąta.

Krótszą diagonalę możemy obliczyć, korzystając z własności trójkąta równobocznego i twierdzenia Pitagorasa. Wyobraźmy sobie, że krótsza diagonala jest podstawą trójkąta równoramiennego, którego ramiona są bokami sześciokąta. Wysokość tego trójkąta dzieli go na dwa trójkąty prostokątne. Długość połowy podstawy (czyli połowy krótszej diagonali) możemy obliczyć, odejmując od kąta 120 stopni kąt prosty 90 stopni, co daje nam trójkąt o kątach 30, 60 i 90 stopni. Stosunek boków w takim trójkącie wynosi 1:√3:2. Zatem wysokość trójkąta równoramiennego, będąca również bokiem trójkąta prostokątnego, ma długość √3 (ponieważ bok trójkąta równoramiennego ma długość 2). Teraz możemy obliczyć długość połowy krótszej diagonali, korzystając z twierdzenia Pitagorasa: a^2 + (√3)^2 = 2^2, a^2 + 3 = 4, a^2 = 1, a = 1. Zatem cała krótsza diagonala ma długość 2√3. Możemy również obliczyć ją, korzystając bezpośrednio z własności sześciokąta foremnego – krótsza diagonala jest √3 razy dłuższa od boku, czyli 2√3.

<h2>Pole Sześciokąta Foremnego</h2>

Kolejną ważną cechą sześciokąta foremnego jest jego pole. Istnieje kilka sposobów na obliczenie pola sześciokąta foremnego o boku 2. Najprostszym jest podzielenie sześciokąta na sześć trójkątów równobocznych o boku równym 2. Pole trójkąta równobocznego o boku a wyraża się wzorem (a^2 * √3) / 4. W naszym przypadku a = 2, więc pole jednego trójkąta równobocznego wynosi (2^2 * √3) / 4 = (4 * √3) / 4 = √3. Ponieważ mamy sześć takich trójkątów, pole całego sześciokąta wynosi 6 * √3.

Innym sposobem obliczenia pola sześciokąta foremnego jest wykorzystanie wzoru P = (3√3 * a^2) / 2, gdzie a to długość boku. W naszym przypadku a = 2, więc P = (3√3 * 2^2) / 2 = (3√3 * 4) / 2 = 12√3 / 2 = 6√3.

Sześciokąt foremny posiada środek symetrii i sześć osi symetrii. Trzy z tych osi przechodzą przez pary przeciwległych wierzchołków, a trzy przez środki przeciwległych boków.

Możemy również spróbować wpisać okrąg w sześciokąt foremny. Środek okręgu wpisanego pokrywa się ze środkiem sześciokąta. Promień okręgu wpisanego jest równy odległości od środka sześciokąta do środka dowolnego z jego boków. Zauważmy, że ten promień jest również wysokością trójkąta równobocznego o boku 2, na który podzieliliśmy sześciokąt. Zatem promień okręgu wpisanego wynosi √3.

Podobnie, możemy opisać okrąg na sześciokącie foremnym. Środek okręgu opisanego również pokrywa się ze środkiem sześciokąta. Promień okręgu opisanego jest równy odległości od środka sześciokąta do dowolnego z jego wierzchołków. Zauważmy, że ten promień jest równy długości boku trójkąta równobocznego, na który podzieliliśmy sześciokąt, czyli wynosi 2.

<h2>Zastosowania Sześciokątów Foremnych</h2>

Sześciokąty foremne znajdują szerokie zastosowanie w różnych dziedzinach. Ze względu na ich regularność i efektywne wykorzystanie przestrzeni, często pojawiają się w naturze, na przykład w plastrach miodu budowanych przez pszczoły. Konstrukcja plastrów miodu w kształcie sześciokątów pozwala pszczołom na maksymalne wykorzystanie przestrzeni i minimalizację zużycia wosku.

W architekturze i budownictwie, sześciokąty foremne są wykorzystywane jako elementy dekoracyjne i konstrukcyjne. Można je znaleźć w mozaikach, posadzkach, a nawet w konstrukcjach dachów i ścian.

W grafice komputerowej i projektowaniu gier, sześciokąty foremne są często wykorzystywane do tworzenia map i siatek, ponieważ pozwalają na równomierne pokrycie powierzchni i łatwe obliczanie odległości.

W chemii, sześciokąt foremny jest podstawowym elementem struktury benzenu, który jest jednym z najważniejszych związków organicznych.

Sześciokąty foremne pojawiają się również w różnych grach i zabawach, takich jak układanki i gry logiczne.

Podsumowując, sześciokąt foremny o boku równym 2 to figura geometryczna, która posiada wiele interesujących własności i znajduje szerokie zastosowanie w różnych dziedzinach. Znając długość boku, możemy obliczyć jego obwód, pole, długości diagonali, promień okręgu wpisanego i opisanego, a także wiele innych parametrów. Sześciokąt foremny jest przykładem figury geometrycznej, która łączy w sobie prostotę i elegancję, a jednocześnie posiada wiele praktycznych zastosowań.

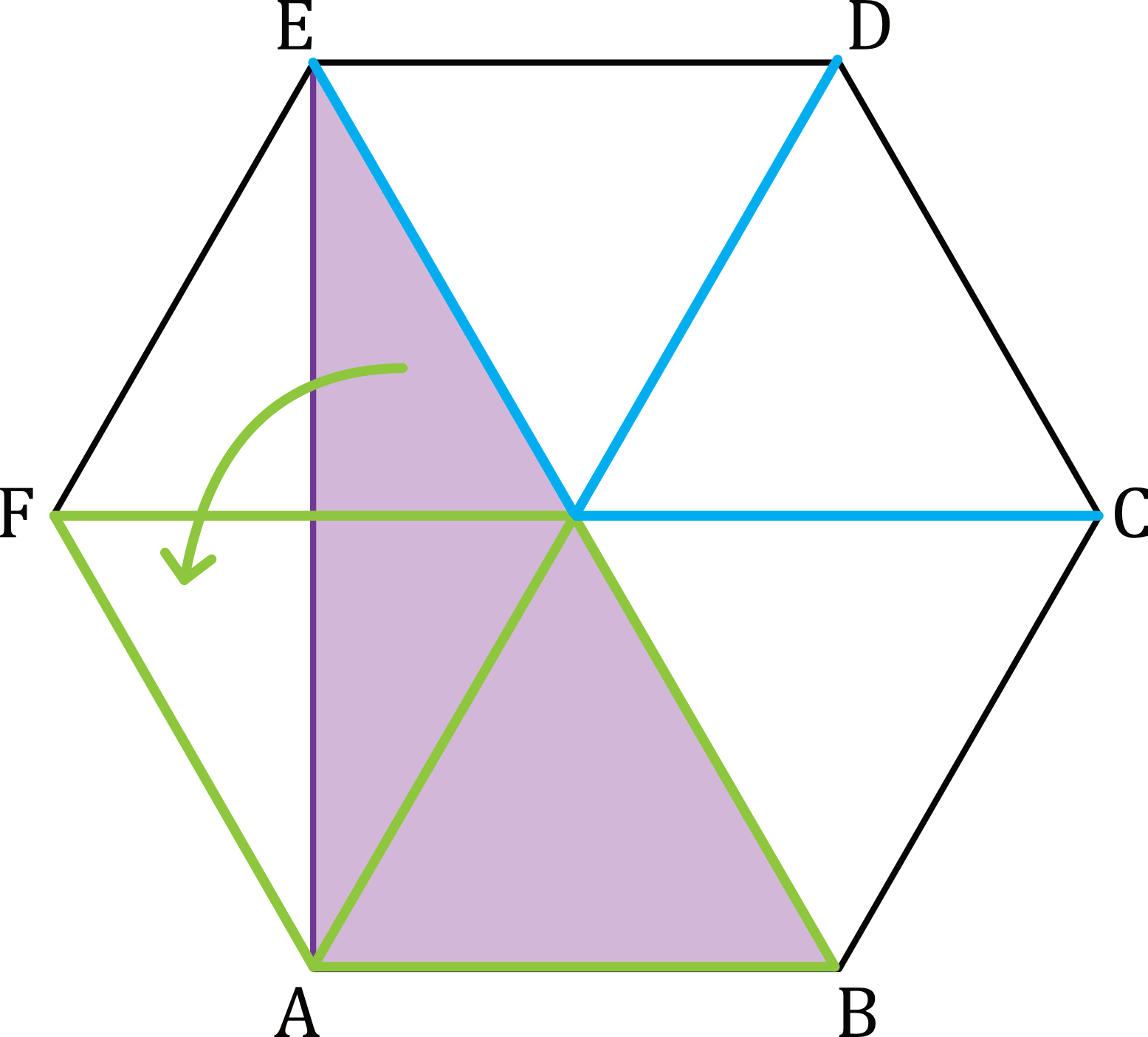
<h2>Podział na Mniejsze Figury</h2>

Rozważmy jeszcze możliwość podziału naszego sześciokąta foremnego o boku 2 na mniejsze figury. Jak już wspomniano, możemy go podzielić na sześć trójkątów równobocznych. Ale czy istnieją inne możliwości?

Możemy podzielić sześciokąt na trapezy równoramienne. Przeciągając odcinki równoległe do dwóch przeciwległych boków, przechodzące przez środek sześciokąta, możemy podzielić go na trzy identyczne trapezy równoramienne. Wysokość każdego trapezu wynosi √3, a podstawy mają długości 2 i 4. Pole każdego trapezu można obliczyć ze wzoru (a+b)h/2, gdzie a i b to długości podstaw, a h to wysokość. Zatem pole jednego trapezu wynosi (2+4)√3/2 = 6√3/2 = 3√3. Suma pól trzech trapezów daje nam pole całego sześciokąta, czyli 3 * 3√3 = 9√3. Coś jest nie tak! Gdzie popełniliśmy błąd?

Błąd polega na tym, że te trapezy nie wypełniają całego sześciokąta. Opisany podział nie jest poprawny.

Wracając do podziału na sześć trójkątów równobocznych, możemy zauważyć, że każdy trójkąt równoboczny można podzielić na dwa trójkąty prostokątne o kątach 30, 60 i 90 stopni. Zatem sześciokąt foremny można podzielić na 12 takich trójkątów prostokątnych.

Możemy również podzielić sześciokąt na prostokąt i dwa trójkąty prostokątne. Rysując prostokąt wpisany w sześciokąt, tak aby jego dłuższe boki były równoległe do dwóch przeciwległych boków sześciokąta, otrzymamy prostokąt o bokach 2 i 2√3. Pole tego prostokąta wynosi 4√3. Pozostałe dwa trójkąty prostokątne są identyczne i każdy z nich ma pole równe √3. Zatem pole całego sześciokąta wynosi 4√3 + √3 + √3 = 6√3.

Analiza różnych podziałów sześciokąta foremnego pozwala na lepsze zrozumienie jego geometrii i własności. Każdy podział ujawnia inne aspekty tej figury i pozwala na wykorzystanie różnych metod obliczeniowych.

Wiedza o własnościach sześciokąta foremnego o boku równym 2 pozwala na rozwiązywanie różnorodnych problemów geometrycznych i praktycznych, a także na lepsze zrozumienie otaczającego nas świata, w którym sześciokąty foremne występują w wielu miejscach, od struktury plastrów miodu po konstrukcje architektoniczne.