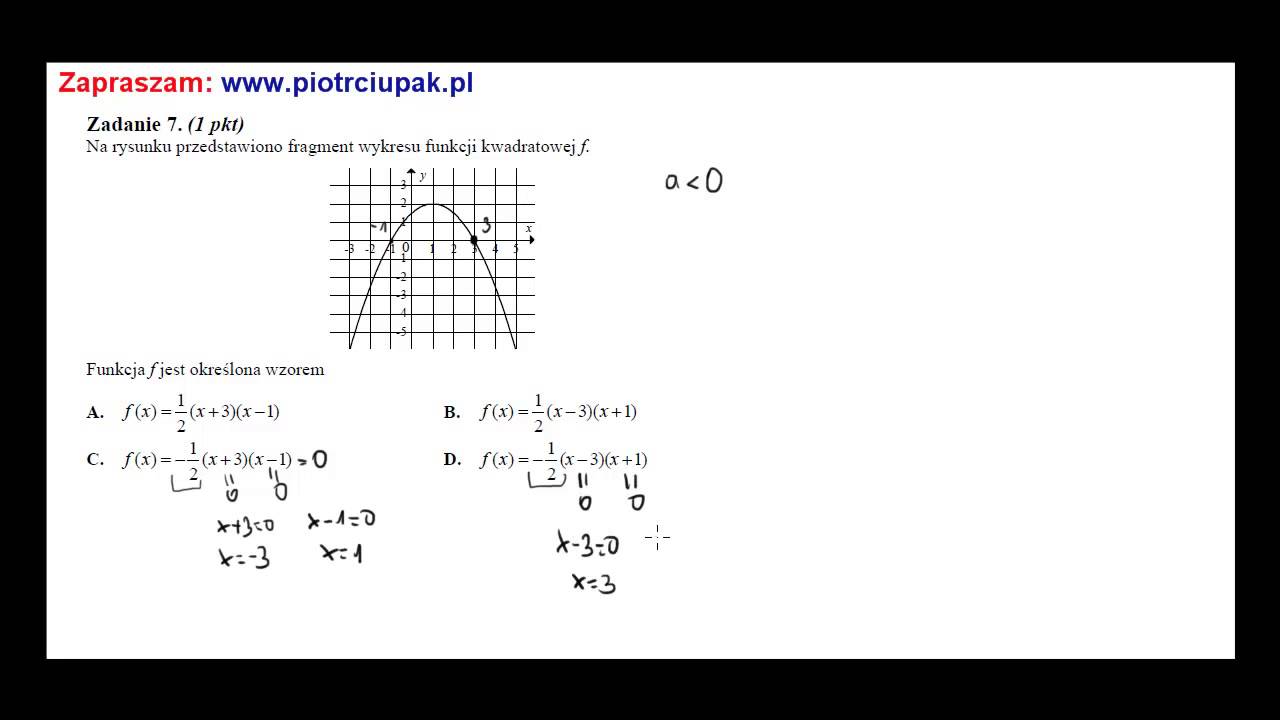
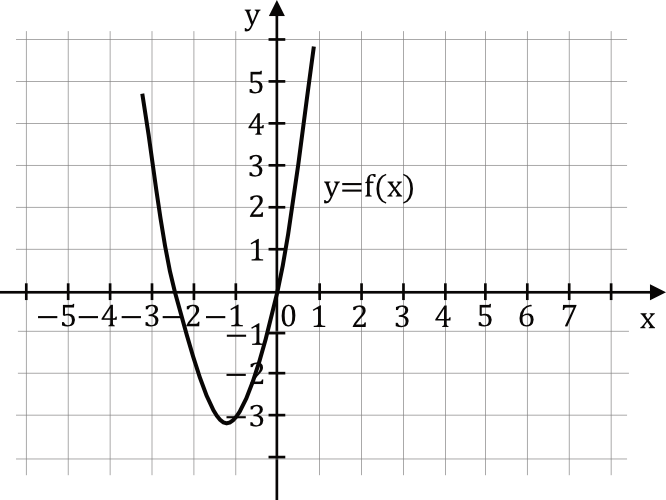
Na Rysunku Przedstawiono Fragment Wykresu Funkcji Kwadratowej F

Okej, postaram się odpowiedzieć na typowe pytania uczniów dotyczące fragmentu wykresu funkcji kwadratowej, przedstawionego na rysunku, w sposób prosty i zrozumiały.

Mamy dany fragment wykresu funkcji kwadratowej f. Z samego rysunku możemy wyciągnąć wiele informacji, które pomogą nam zrozumieć tę funkcję i rozwiązywać związane z nią zadania. Najczęściej spotykane pytania dotyczą miejsc zerowych, wierzchołka paraboli, osi symetrii, wzoru funkcji (w różnych postaciach), zbioru wartości, przedziałów monotoniczności (wzrastania i malejenia), wartości największej i najmniejszej (jeśli są w danym przedziale) oraz znaku funkcji w różnych przedziałach.

Odczytywanie informacji z wykresu

Na początek, przyjrzyjmy się, co możemy bezpośrednio odczytać z wykresu. Najczęściej rysunek przedstawia parabolę, która przecina oś OX (oś x) w jednym lub dwóch punktach, albo wcale. Te punkty przecięcia to miejsca zerowe funkcji. Jeżeli parabola dotyka osi OX w jednym punkcie, to mówimy o jednym miejscu zerowym (podwójnym). Jeżeli parabola nie przecina osi OX, funkcja nie ma miejsc zerowych (w zbiorze liczb rzeczywistych).

Spójrzmy na wierzchołek paraboli. To jest ten najbardziej charakterystyczny punkt - "szczyt" (dla paraboli skierowanej ramionami do dołu) albo "dół" (dla paraboli skierowanej ramionami do góry). Współrzędne wierzchołka oznaczamy jako (p, q). Wierzchołek jest kluczowy, ponieważ pozwala nam określić oś symetrii paraboli.

Oś symetrii to prosta pionowa, która przechodzi przez wierzchołek paraboli. Jej równanie to x = p (gdzie p to współrzędna x wierzchołka). Oś symetrii dzieli parabolę na dwie identyczne połówki.

Przedziały monotoniczności

Parabola albo rośnie, albo maleje (albo jest stała, ale to nie dotyczy funkcji kwadratowej). Patrzymy na wykres od lewej do prawej. Jeśli linia wykresu idzie w górę, to funkcja rośnie. Jeśli linia wykresu idzie w dół, to funkcja maleje. Ważne jest, aby określić, gdzie funkcja rośnie i maleje. Pomaga nam w tym wierzchołek. Na przykład, jeśli ramiona paraboli są skierowane do góry, to funkcja maleje od minus nieskończoności do x wierzchołka, a rośnie od x wierzchołka do plus nieskończoności. Musisz patrzeć na konkretny wykres i zauważyć, w którą stronę skierowane są ramiona paraboli.

Zbiór wartości

Zbiór wartości to wszystkie możliwe wartości y, które przyjmuje funkcja. Patrzymy, jak "wysoko" i "nisko" sięga wykres. Jeśli ramiona paraboli są skierowane do góry, to najniższą wartością jest y wierzchołka (q), a wykres "sięga" do plus nieskończoności. Zatem zbiór wartości to <q, +∞). Jeśli ramiona są skierowane do dołu, to najwyższą wartością jest y wierzchołka (q), a wykres "sięga" do minus nieskończoności. Zatem zbiór wartości to (-∞, q>.

Wartości funkcji w danym przedziale

Czasami pytanie dotyczy wartości największej lub najmniejszej funkcji w określonym przedziale. Trzeba zobaczyć, czy wierzchołek paraboli leży w tym przedziale. Jeśli tak, to wartość funkcji w wierzchołku (q) jest albo wartością największą (jeśli ramiona skierowane w dół), albo najmniejszą (jeśli ramiona skierowane do góry). Jeśli wierzchołek NIE leży w przedziale, to trzeba sprawdzić wartości funkcji na końcach przedziału i wybrać większą lub mniejszą z nich.

Znak funkcji

Pytanie o znak funkcji to pytanie, kiedy funkcja jest dodatnia (wykres leży nad osią OX), a kiedy ujemna (wykres leży pod osią OX). Jeżeli funkcja ma miejsca zerowe, to one dzielą oś OX na przedziały, w których funkcja ma stały znak (albo dodatni, albo ujemny). Patrzysz, czy w danym przedziale wykres jest nad, czy pod osią OX.

Różne postacie wzoru funkcji kwadratowej

Funkcję kwadratową można zapisać na kilka sposobów:

Postać ogólna: f(x) = ax² + bx + c
Postać kanoniczna (wierzchołkowa): f(x) = a(x - p)² + q (gdzie (p, q) to wierzchołek)
Postać iloczynowa (jeśli istnieją miejsca zerowe): f(x) = a(x - x₁) (x - x₂) (gdzie x₁ i x₂ to miejsca zerowe)

Z rysunku najłatwiej odczytać informacje potrzebne do zapisu w postaci kanonicznej (współrzędne wierzchołka) oraz iloczynowej (miejsca zerowe). Żeby znaleźć współczynniki w postaci ogólnej, trzeba zwykle rozwiązać układ równań, mając dane np. współrzędne wierzchołka i jednego dodatkowego punktu na wykresie.

Przechodzenie między postaciami wzoru

Załóżmy, że mamy postać kanoniczną f(x) = a(x - p)² + q i chcemy przejść do postaci ogólnej. Wystarczy rozwinąć wzór:

f(x) = a(x² - 2px + p²) + q f(x) = ax² - 2apx + ap² + q

Teraz możemy zidentyfikować współczynniki: a (w obu postaciach taki sam) b = -2ap c = ap² + q

Podobnie, mając postać iloczynową f(x) = a(x - x₁) (x - x₂), możemy przejść do postaci ogólnej:

f(x) = a(x² - x₂x - x₁x + x₁x₂) f(x) = a(x² - (x₁ + x₂)x + x₁x₂) f(x) = ax² - a(x₁ + x₂)x + ax₁x₂

Współczynniki: a (w obu postaciach taki sam) b = -a(x₁ + x₂) c = ax₁x₂

Przykładowe zadania i jak je rozwiązywać

Zadanie 1: Na rysunku przedstawiono fragment paraboli, której wierzchołek ma współrzędne (2, -1). Parabola przechodzi przez punkt (0, 3). Znajdź wzór funkcji w postaci kanonicznej i ogólnej.

Rozwiązanie:

Wierzchołek to (2, -1), więc p = 2 i q = -1. Postać kanoniczna to f(x) = a(x - 2)² - 1.
Parabola przechodzi przez punkt (0, 3), więc f(0) = 3. Podstawiamy do postaci kanonicznej: 3 = a(0 - 2)² - 1.
Rozwiązujemy równanie: 3 = 4a - 1 => 4a = 4 => a = 1.
Postać kanoniczna: f(x) = (x - 2)² - 1.
Przechodzimy do postaci ogólnej: f(x) = x² - 4x + 4 - 1 = x² - 4x + 3.

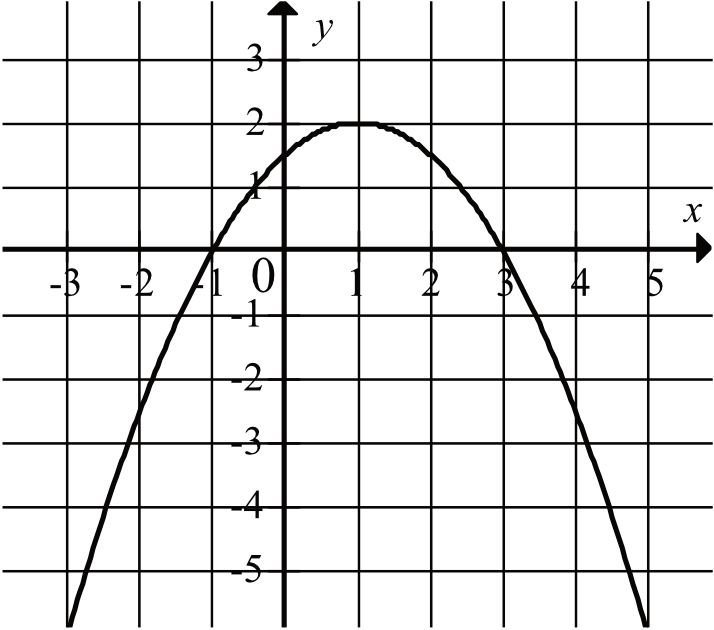
Zadanie 2: Na rysunku przedstawiono fragment paraboli przecinającej oś OX w punktach -1 i 3. Parabola przechodzi przez punkt (0, -3). Znajdź wzór funkcji w postaci iloczynowej i ogólnej.

Rozwiązanie:

Miejsca zerowe to -1 i 3, więc postać iloczynowa to f(x) = a(x + 1)(x - 3).
Parabola przechodzi przez punkt (0, -3), więc f(0) = -3. Podstawiamy do postaci iloczynowej: -3 = a(0 + 1)(0 - 3).
Rozwiązujemy równanie: -3 = -3a => a = 1.
Postać iloczynowa: f(x) = (x + 1)(x - 3).
Przechodzimy do postaci ogólnej: f(x) = x² - 3x + x - 3 = x² - 2x - 3.

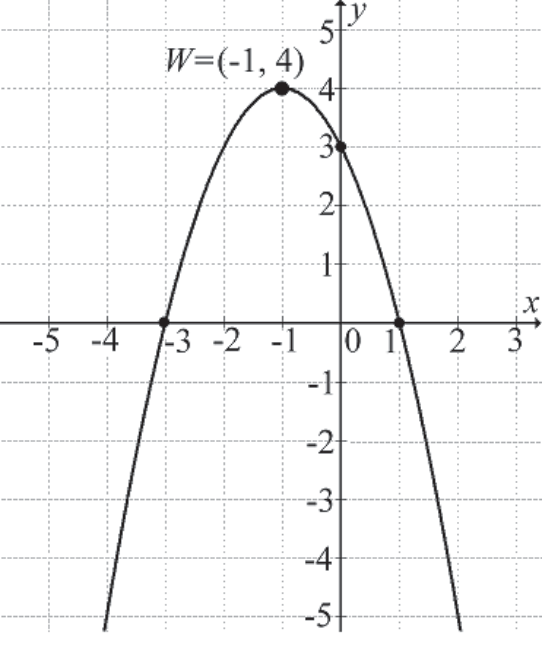
Zadanie 3: Na rysunku widać parabolę z ramionami skierowanymi w dół. Wierzchołek ma współrzędne (1, 4). Podaj zbiór wartości funkcji.

Rozwiązanie:

Ramiona skierowane w dół, więc parabola ma wartość największą w wierzchołku.
Wartość y wierzchołka to 4.
Zbiór wartości to (-∞, 4>.

Mam nadzieję, że te wyjaśnienia i przykłady pomogą Ci lepiej zrozumieć, jak analizować fragment wykresu funkcji kwadratowej i rozwiązywać związane z nim zadania. Pamiętaj, że kluczem jest dokładne odczytywanie informacji z rysunku i umiejętność posługiwania się różnymi postaciami wzoru funkcji kwadratowej. Powodzenia!