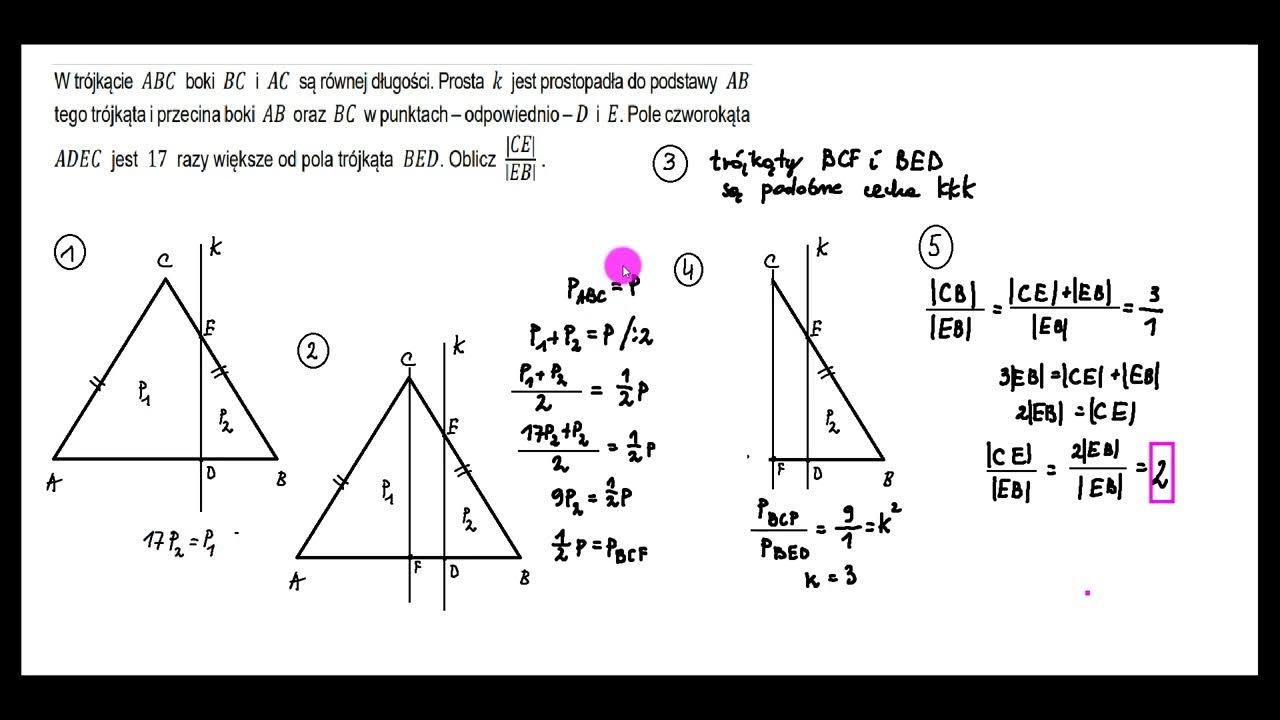
Na Rysunku Przedstawiona Jest Prosta K

Czy kiedykolwiek zastanawiałeś się, jak jeden prosty rysunek może kryć w sobie bogactwo informacji i stanowić fundament do zrozumienia bardziej złożonych zagadnień matematycznych? Dziś skupimy się na jednym konkretnym elemencie: prostej k. Naszym celem jest demistyfikacja tej prostej, zrozumienie jej cech i nauczenie się, jak wykorzystać ją do rozwiązywania problemów. Ten artykuł skierowany jest do uczniów szkół podstawowych i średnich, a także do wszystkich tych, którzy chcą odświeżyć swoje wiadomości z geometrii.

Czym Jest Prosta?

Zanim zagłębimy się w analizę prostej k, warto przypomnieć sobie, czym w ogóle jest prosta w matematyce. Najprościej mówiąc, prosta to nieskończona linia, która rozciąga się w obu kierunkach bez końca. Nie ma początku ani końca i jest definiowana przez co najmniej dwa punkty. Wyobraź sobie promień światła laserowego – teoretycznie, biegnie on w nieskończoność.

Ważne cechy prostej:

Nieskończona długość: Nie ma końca.
Brak krzywizny: Jest idealnie prosta.
Definiowana przez dwa punkty: Przez dwa różne punkty na płaszczyźnie przechodzi dokładnie jedna prosta.

Analiza Rysunku z Prostą k

Załóżmy, że mamy rysunek, na którym widoczna jest prosta k. Aby skutecznie ją analizować, musimy zwrócić uwagę na kilka kluczowych elementów.

Położenie Prostej k na Rysunku

Pierwsze pytanie, które powinniśmy sobie zadać, to: jak prosta k jest zorientowana w przestrzeni? Czy jest pozioma, pionowa, czy nachylona pod pewnym kątem? Orientacja prostej k ma ogromne znaczenie, szczególnie gdy będziemy analizować jej równanie lub szukać punktów przecięcia z innymi prostymi lub osiami układu współrzędnych.

Punkty Leżące na Prostej k

Następnie, poszukajmy punktów, które wyraźnie leżą na prostej k. Mogą to być punkty zaznaczone na rysunku, lub punkty, które możemy z łatwością odczytać, korzystając z układu współrzędnych. Znając współrzędne dwóch punktów leżących na prostej, możemy wyznaczyć jej równanie.

Na przykład, jeśli na prostej k widzimy punkty A(1, 2) i B(3, 4), to możemy z tych informacji obliczyć równanie tej prostej. To niezwykle ważna umiejętność w rozwiązywaniu zadań z geometrii analitycznej.

Punkty Przecięcia z Osiami Układu Współrzędnych

Sprawdźmy, czy prosta k przecina osie układu współrzędnych (oś X i oś Y). Punkty przecięcia z osiami są szczególnie ważne, ponieważ pozwalają nam określić tzw. współrzędne charakterystyczne prostej. Punkt przecięcia z osią Y nazywamy wyrazem wolnym w równaniu prostej, a punkt przecięcia z osią X (o ile istnieje) to miejsce zerowe funkcji liniowej reprezentowanej przez tę prostą.

Inne Obiekty Geometryczne na Rysunku

Zwróćmy uwagę, czy na rysunku, poza prostą k, znajdują się inne obiekty geometryczne, takie jak inne proste, okręgi, trójkąty, czy kwadraty. Relacja pomiędzy prostą k a tymi obiektami może być kluczowa do rozwiązania zadania. Czy prosta k jest prostopadła do innej prostej? Czy przecina okrąg w dwóch punktach? Czy jest styczna do okręgu? Odpowiedzi na te pytania pomogą nam zrozumieć sytuację przedstawioną na rysunku.

Równanie Prostej k

Jednym z najważniejszych aspektów analizy prostej k jest znalezienie jej równania. Istnieje kilka sposobów, aby to zrobić, w zależności od danych, które mamy do dyspozycji.

Równanie Kierunkowe Prostej

Najpopularniejszą formą równania prostej jest równanie kierunkowe: y = ax + b, gdzie:

a to współczynnik kierunkowy, który mówi nam o nachyleniu prostej (jak szybko rośnie lub maleje wartość y, gdy x rośnie).
b to wyraz wolny, który określa punkt przecięcia prostej z osią Y.

Jeśli znamy dwa punkty leżące na prostej k, możemy obliczyć współczynnik kierunkowy a ze wzoru: a = (y2 - y1) / (x2 - x1), gdzie (x1, y1) i (x2, y2) to współrzędne tych punktów. Następnie, możemy podstawić współrzędne jednego z tych punktów oraz obliczony współczynnik kierunkowy do równania y = ax + b i obliczyć wyraz wolny b.

Równanie Ogólne Prostej

Inną formą równania prostej jest równanie ogólne: Ax + By + C = 0, gdzie A, B i C to współczynniki liczbowe. Równanie to jest bardziej ogólne, ponieważ pozwala opisać również proste pionowe (których nie można opisać za pomocą równania kierunkowego).

Aby przejść z równania kierunkowego do równania ogólnego, wystarczy przekształcić równanie y = ax + b w postać Ax + By + C = 0. Na przykład, równanie y = 2x + 3 możemy zapisać jako -2x + y - 3 = 0.

Równanie Prostej Przechodzącej Przez Dwa Punkty

Jeśli znamy współrzędne dwóch punktów A(x1, y1) i B(x2, y2) leżących na prostej k, możemy od razu napisać jej równanie korzystając z wzoru:

(y - y1) / (x - x1) = (y2 - y1) / (x2 - x1)

Po przekształceniu tego równania, otrzymamy równanie prostej w postaci ogólnej lub kierunkowej.

Przykładowe Zadania i Rozwiązania

Aby lepiej zrozumieć, jak analizować prostą k na rysunku, przeanalizujmy kilka przykładowych zadań.

Zadanie 1:

Na rysunku przedstawiona jest prosta k przechodząca przez punkty A(2, 1) i B(4, 5). Znajdź równanie tej prostej w postaci kierunkowej.

Rozwiązanie:

Obliczamy współczynnik kierunkowy a: a = (5 - 1) / (4 - 2) = 4 / 2 = 2
Podstawiamy współrzędne punktu A (2, 1) i współczynnik kierunkowy a = 2 do równania y = ax + b: 1 = 2 * 2 + b
Obliczamy wyraz wolny b: 1 = 4 + b => b = -3
Otrzymujemy równanie prostej k: y = 2x - 3

Zadanie 2:

Na rysunku przedstawiona jest prosta k o równaniu y = -x + 2. Znajdź punkt przecięcia tej prostej z osią X.

Rozwiązanie:

Punkt przecięcia z osią X ma współrzędną y równą 0. Zatem, musimy rozwiązać równanie: 0 = -x + 2
Przekształcamy równanie: x = 2
Punkt przecięcia prostej k z osią X to (2, 0).

Dlaczego To Jest Ważne?

Umiejętność analizowania rysunku z prostą k i wyznaczania jej równania jest fundamentalna w wielu dziedzinach nauki i techniki. Wykorzystywana jest w:

Matematyce: Podstawą geometrii analitycznej, algebry liniowej, analizy matematycznej.
Fizyce: Opis ruchu jednostajnego prostoliniowego, analizy wykresów zależności fizycznych.
Informatyce: Grafika komputerowa, algorytmy, tworzenie gier.
Inżynierii: Projektowanie konstrukcji, obliczenia statyczne.

Zrozumienie prostej k to krok w kierunku opanowania bardziej zaawansowanych zagadnień matematycznych i technicznych. To narzędzie, które otwiera drzwi do wielu fascynujących obszarów wiedzy.

Podsumowanie i Wartości Dodane

W tym artykule przyjrzeliśmy się bliżej prostej k przedstawionej na rysunku. Omówiliśmy, jak analizować jej położenie, identyfikować punkty leżące na prostej, znajdować punkty przecięcia z osiami układu współrzędnych oraz wyznaczać jej równanie. Przeanalizowaliśmy również kilka przykładowych zadań, aby zilustrować praktyczne zastosowanie zdobytej wiedzy.

Pamiętaj, że kluczem do sukcesu w matematyce jest praktyka. Im więcej zadań rozwiążesz, tym lepiej zrozumiesz zagadnienia i tym pewniej będziesz się czuł w rozwiązywaniu problemów. Zachęcamy Cię do dalszego eksplorowania świata matematyki i wykorzystywania wiedzy o prostej k do rozwiązywania coraz bardziej skomplikowanych zadań. Powodzenia!