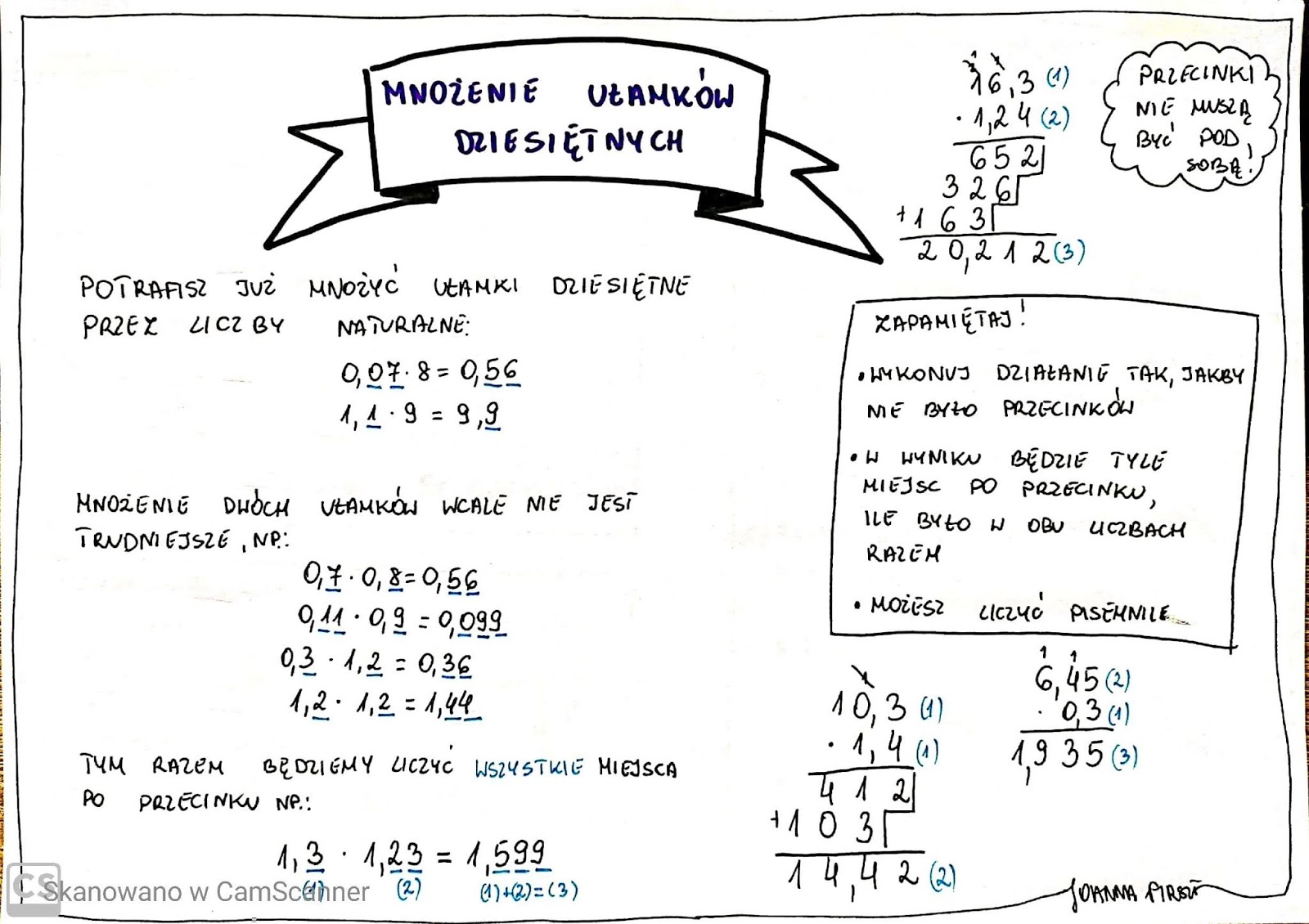
Mnożenie Ułamków Dziesiętnych Przez Liczby Naturalne Klasa 5

Witajcie, młodzi matematycy! Dziś zajmiemy się mnożeniem ułamków dziesiętnych przez liczby naturalne. To nic trudnego, obiecuję! Przekonacie się, że to bardzo podobne do zwykłego mnożenia, które już znacie.

Zacznijmy od prostego przykładu: 0,2 x 3.

Wyobraźcie sobie, że macie trzy monety po 20 groszy każda. Ile macie groszy razem? 60 groszy, prawda? To dokładnie to samo, co 0,2 x 3 = 0,6.

Spójrzmy na kolejny przykład: 1,5 x 2.

Możecie pomyśleć o tym jak o dwóch batonach, które kosztują po 1,5 złotego każdy. Ile zapłacicie za te batony? 3 złote. Więc 1,5 x 2 = 3.

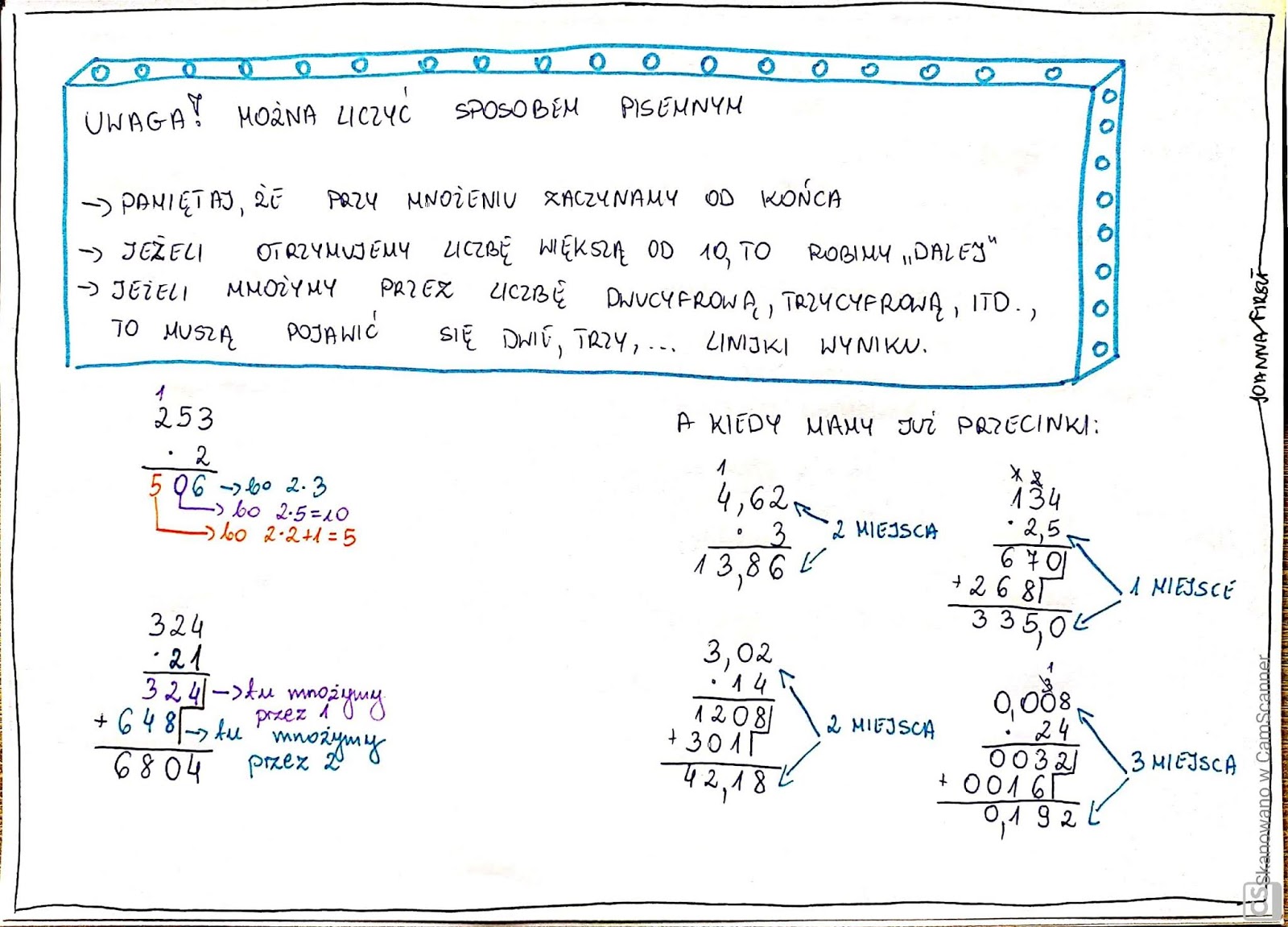
To, co robimy, to w zasadzie mnożymy liczbę bez przecinka, a potem musimy tylko pamiętać o umieszczeniu przecinka we właściwym miejscu.

Weźmy przykład: 2,34 x 4.

Najpierw pomijamy przecinek i mnożymy 234 x 4.

234 x 4 = 936

Teraz musimy zastanowić się, gdzie umieścić przecinek. W liczbie 2,34 mamy dwa miejsca po przecinku (3 i 4). Oznacza to, że w naszym wyniku, 936, musimy również odliczyć dwa miejsca od końca i tam umieścić przecinek.

Więc 2,34 x 4 = 9,36

Widzicie, to naprawdę proste!

Spróbujmy z trudniejszym przykładem: 12,05 x 7.

Znowu pomijamy przecinek i mnożymy 1205 x 7.

1205 x 7 = 8435

W liczbie 12,05 mamy dwa miejsca po przecinku (0 i 5). Zatem w wyniku 8435 musimy odliczyć dwa miejsca od końca i tam wstawić przecinek.

Więc 12,05 x 7 = 84,35

Zauważcie, że liczba naturalna, przez którą mnożymy, nie ma przecinka. Przecinek pojawia się tylko w ułamku dziesiętnym.

Co się dzieje, jeśli mamy zero na końcu po przecinku? Na przykład 3,50 x 2?

Mnożymy 350 x 2 = 700

Mamy dwa miejsca po przecinku w liczbie 3,50 (5 i 0). Odliczamy dwa miejsca od końca w 700 i otrzymujemy 7,00.

Pamiętajcie, że zera na końcu po przecinku możemy pominąć. Więc 7,00 to to samo co 7.

Dlatego 3,50 x 2 = 7.

Jak to działa w praktyce?

Spróbujmy rozwiązać kilka zadań tekstowych, żeby zobaczyć, jak możemy wykorzystać tę wiedzę w życiu codziennym.

Zadanie 1:

Kasia kupiła 5 lizaków. Każdy lizak kosztował 1,25 zł. Ile Kasia zapłaciła za lizaki?

Musimy pomnożyć 1,25 x 5.

Pomijamy przecinek i mnożymy 125 x 5 = 625

W liczbie 1,25 mamy dwa miejsca po przecinku. Odliczamy dwa miejsca od końca w 625 i wstawiamy przecinek.

Dostajemy 6,25.

Odpowiedź: Kasia zapłaciła 6,25 zł za lizaki.

Zadanie 2:

Jeden kilogram jabłek kosztuje 2,80 zł. Mama kupiła 3 kg jabłek. Ile mama zapłaciła za jabłka?

Musimy pomnożyć 2,80 x 3.

Pomijamy przecinek i mnożymy 280 x 3 = 840

W liczbie 2,80 mamy dwa miejsca po przecinku. Odliczamy dwa miejsca od końca w 840 i wstawiamy przecinek.

Dostajemy 8,40.

Odpowiedź: Mama zapłaciła 8,40 zł za jabłka.

Zadanie 3:

Pan Jan przejechał samochodem 4 odcinki trasy. Każdy odcinek miał długość 15,7 km. Ile kilometrów przejechał pan Jan?

Musimy pomnożyć 15,7 x 4.

Pomijamy przecinek i mnożymy 157 x 4 = 628

W liczbie 15,7 mamy jedno miejsce po przecinku. Odliczamy jedno miejsce od końca w 628 i wstawiamy przecinek.

Dostajemy 62,8.

Odpowiedź: Pan Jan przejechał 62,8 km.

Pamiętajcie, że kluczem do sukcesu jest regularna praktyka. Im więcej zadań rozwiążecie, tym łatwiej będzie Wam mnożyć ułamki dziesiętne przez liczby naturalne.

Ważne jest również, aby zwracać uwagę na to, co robimy. Czy wynik ma sens? Jeśli mnożymy 0,5 x 4, to spodziewamy się wyniku większego niż 0,5, ale mniejszego niż 4. Sprawdzanie, czy wynik jest logiczny, pomoże nam uniknąć błędów.

Mnożenie ułamków dziesiętnych przez liczby naturalne to bardzo przydatna umiejętność. Używamy jej w sklepie, przy obliczaniu kosztów podróży, a nawet podczas gotowania! Dlatego warto poświęcić trochę czasu na opanowanie tej umiejętności.

Podsumowując: