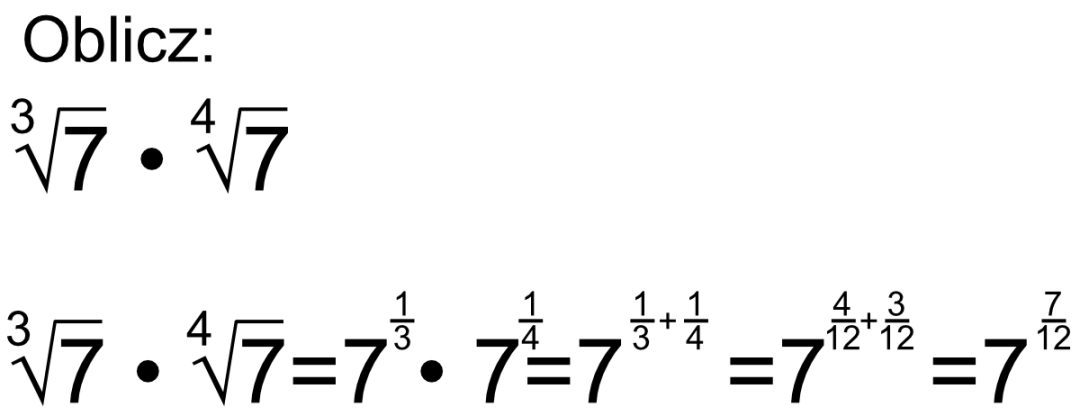Mnożenie Pierwiastka Przez Liczbę Całkowitą

Czy kiedykolwiek zastanawiałeś się, jak uprościć wyrażenie, w którym pierwiastek miesza się z liczbą całkowitą? Może wydaje się to skomplikowane, ale w rzeczywistości mnożenie pierwiastka przez liczbę całkowitą jest prostym i użytecznym narzędziem matematycznym. W tym artykule przyjrzymy się, jak to zrobić, dlaczego to działa i gdzie możesz to zastosować. Artykuł ten jest przeznaczony dla uczniów szkół średnich, studentów oraz wszystkich, którzy chcą odświeżyć swoje umiejętności matematyczne i lepiej zrozumieć operacje na pierwiastkach.

Co to jest pierwiastek?

Zanim przejdziemy do mnożenia, przypomnijmy sobie, czym jest pierwiastek. Mówiąc najprościej, pierwiastek kwadratowy z liczby x to taka liczba, która pomnożona przez samą siebie daje x. Na przykład, pierwiastek kwadratowy z 9 to 3, ponieważ 3 * 3 = 9. Matematycznie zapisujemy to jako √9 = 3. Istnieją również pierwiastki wyższych stopni, np. pierwiastek trzeciego stopnia (sześcienny), oznaczany jako ∛.

Warto pamiętać, że pierwiastki mogą być liczbami całkowitymi (np. √4 = 2), ale także liczbami niewymiernymi (np. √2 ≈ 1.4142). Liczby niewymierne nie dają się zapisać jako ułamek zwykły, a ich rozwinięcie dziesiętne jest nieskończone i nieokresowe.

Mnożenie pierwiastka przez liczbę całkowitą – zasady

Mnożenie pierwiastka przez liczbę całkowitą jest bardzo proste. Wyobraź sobie, że masz wyrażenie a√b, gdzie a to liczba całkowita, a √b to pierwiastek. W takim przypadku, a po prostu staje się współczynnikiem przed pierwiastkiem. Nie możemy "wmieszać" go bezpośrednio pod znak pierwiastka, chyba że podniesiemy go do potęgi odpowiadającej stopniowi pierwiastka.

Przykład:

3√5 to po prostu "trzy pierwiastki z pięciu". Nie możemy obliczyć √5 bez kalkulatora (otrzymamy liczbę niewymierną), więc wyrażenie 3√5 pozostawiamy w takiej postaci.

Jeżeli chcemy wprowadzić liczbę całkowitą pod pierwiastek, musimy wykonać odpowiednią operację. Na przykład:

W przypadku pierwiastka kwadratowego, podnosimy liczbę całkowitą do kwadratu i mnożymy przez liczbę pod pierwiastkiem: a√b = √(a² * b)
W przypadku pierwiastka trzeciego stopnia, podnosimy liczbę całkowitą do potęgi trzeciej i mnożymy przez liczbę pod pierwiastkiem: a∛b = ∛(a³ * b)

Przykłady mnożenia pierwiastka przez liczbę całkowitą

Oto kilka przykładów, które pomogą Ci lepiej zrozumieć:

2√3: To po prostu "dwa pierwiastki z trzech". Jeśli chcemy wprowadzić 2 pod pierwiastek, to 2√3 = √(2² * 3) = √(4 * 3) = √12
5√2: To "pięć pierwiastków z dwóch". Jeśli chcemy wprowadzić 5 pod pierwiastek, to 5√2 = √(5² * 2) = √(25 * 2) = √50
-4√7: To "minus cztery pierwiastki z siedmiu". Jeśli chcemy wprowadzić -4 pod pierwiastek, to -4√7 = -√(4² * 7) = -√(16 * 7) = -√112 (zwróć uwagę na zachowanie znaku minus przed pierwiastkiem).
10∛4: To "dziesięć pierwiastków trzeciego stopnia z czterech". Jeśli chcemy wprowadzić 10 pod pierwiastek, to 10∛4 = ∛(10³ * 4) = ∛(1000 * 4) = ∛4000

Dlaczego to działa?

Zrozumienie, dlaczego możemy mnożyć pierwiastek przez liczbę całkowitą w ten sposób, leży w podstawowych prawach działań na pierwiastkach i potęgach. Kluczową zasadą jest:

√(a * b) = √a * √b

czyli pierwiastek z iloczynu dwóch liczb jest równy iloczynowi pierwiastków z tych liczb. Wykorzystując to prawo, możemy zrozumieć, dlaczego a√b = √(a² * b). W istocie, cofamy się do formy √(a²) * √b, a ponieważ √(a²) = a (dla a dodatniego), wracamy do punktu wyjścia.

Zastosowania mnożenia pierwiastka przez liczbę całkowitą

Mnożenie pierwiastka przez liczbę całkowitą ma wiele praktycznych zastosowań w matematyce i fizyce. Oto kilka przykładów:

Upraszczanie wyrażeń: Często upraszczanie wyrażeń algebraicznych wymaga wyłączenia czynnika przed znak pierwiastka. Na przykład, √75 można uprościć do 5√3. Dzieje się tak, ponieważ 75 = 25 * 3, więc √75 = √(25 * 3) = √25 * √3 = 5√3.
Rozwiązywanie równań: W rozwiązywaniu równań kwadratowych często pojawiają się pierwiastki. Upraszczanie tych pierwiastków pomaga w uzyskaniu bardziej przejrzystych i zrozumiałych rozwiązań.
Geometria: W obliczeniach związanych z długościami boków trójkątów (np. z twierdzenia Pitagorasa) często występują pierwiastki. Upraszczanie ich jest kluczowe do uzyskania dokładnych wyników. Na przykład, jeśli przekątna kwadratu ma długość √8, to możemy uprościć to do 2√2, co jest bardziej zrozumiałe.
Fizyka: W fizyce pierwiastki pojawiają się w różnych wzorach, np. związanych z energią kinetyczną, prędkością czy przyspieszeniem. Upraszczanie wyrażeń z pierwiastkami ułatwia obliczenia i interpretację wyników.

Przykłady praktyczne

Przykład 1: Upraszczanie wyrażenia

Uprość wyrażenie: √18 + 3√2

Zauważamy, że 18 = 9 * 2, więc √18 = √(9 * 2) = √9 * √2 = 3√2
Teraz możemy podstawić to do oryginalnego wyrażenia: 3√2 + 3√2
Dodajemy współczynniki przed pierwiastkiem: (3 + 3)√2 = 6√2
Ostatecznie: √18 + 3√2 = 6√2

Przykład 2: Rozwiązywanie równania

Rozwiąż równanie: x² = 27

Wyciągamy pierwiastek kwadratowy z obu stron: x = ±√27
Upraszczamy √27. Zauważamy, że 27 = 9 * 3, więc √27 = √(9 * 3) = √9 * √3 = 3√3
Ostatecznie: x = ±3√3

Przykład 3: Geometria – obliczanie długości boku trójkąta

W trójkącie prostokątnym jedna przyprostokątna ma długość 2, a przeciwprostokątna ma długość √20. Oblicz długość drugiej przyprostokątnej.

Z twierdzenia Pitagorasa: a² + b² = c², gdzie a i b to przyprostokątne, a c to przeciwprostokątna.
W naszym przypadku: 2² + b² = (√20)²
Upraszczamy: 4 + b² = 20
Odejmujemy 4 od obu stron: b² = 16
Wyciągamy pierwiastek kwadratowy: b = √16 = 4
Jednak, co jeśli mielibyśmy przeciwprostokątną o długości √24 ? Wtedy: 4 + b² = 24, b² = 20, b = √20. Upraszczamy: √20 = √(4 * 5) = √4 * √5 = 2√5.

Wskazówki i triki

Znajdź największy kwadrat/sześcian: Podczas upraszczania pierwiastków, szukaj największego kwadratu (dla pierwiastka kwadratowego) lub sześcianu (dla pierwiastka trzeciego stopnia), który dzieli liczbę pod pierwiastkiem.
Pamiętaj o znaku: Przy wprowadzaniu liczb ujemnych pod pierwiastek, pamiętaj o zachowaniu znaku minus przed pierwiastkiem.
Ćwicz, ćwicz, ćwicz: Im więcej ćwiczysz, tym łatwiej będzie Ci rozpoznawać wzory i upraszczać wyrażenia z pierwiastkami.
Używaj kalkulatora (z głową): Kalkulator może pomóc w sprawdzeniu odpowiedzi, ale staraj się najpierw rozwiązywać zadania ręcznie, aby lepiej zrozumieć proces.

Podsumowanie

Mnożenie pierwiastka przez liczbę całkowitą to podstawowa umiejętność matematyczna, która jest przydatna w wielu dziedzinach. Zrozumienie zasad i regularna praktyka pozwolą Ci na swobodne operowanie pierwiastkami i upraszczanie wyrażeń. Pamiętaj o kluczowych krokach: rozpoznawaniu pierwiastka, wyciąganiu czynnika przed znak pierwiastka, a w razie potrzeby – wprowadzaniu go pod pierwiastek po podniesieniu do odpowiedniej potęgi.

Mamy nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć, jak mnożyć pierwiastek przez liczbę całkowitą. Powodzenia w dalszej nauce matematyki!