Mnożenie I Dzielenie Ułamków Zwykłych Zadania Klasa 6 Pdf

Ułamki zwykłe to fundament matematyki, a opanowanie operacji mnożenia i dzielenia na nich jest kluczowe dla uczniów klasy 6. W tym artykule skupimy się na rozwiązywaniu zadań z zakresu mnożenia i dzielenia ułamków zwykłych, tak jak te, które często pojawiają się w materiałach PDF dla klasy 6. Przygotujcie się na konkretne przykłady i praktyczne ćwiczenia, które pomogą Wam utrwalić wiedzę.

Zacznijmy od mnożenia. Mnożąc ułamki zwykłe, postępujemy stosunkowo prosto. Weźmy przykład:

2/3 * 1/4

Mnożymy licznik przez licznik, a mianownik przez mianownik. Otrzymujemy:

(2 * 1) / (3 * 4) = 2/12

Teraz, jeśli to możliwe, upraszczamy ułamek. W tym przypadku 2/12 można uprościć, dzieląc licznik i mianownik przez 2:

2/12 = 1/6

Kolejny przykład:

5/8 * 3/7

Postępujemy analogicznie:

(5 * 3) / (8 * 7) = 15/56

W tym przypadku ułamka 15/56 nie da się już uprościć.

A co, jeśli mnożymy ułamek przez liczbę całkowitą? Załóżmy, że mamy:

3/4 * 5

W takim przypadku liczbę całkowitą możemy traktować jako ułamek z mianownikiem równym 1:

3/4 * 5/1

Teraz mnożymy normalnie:

(3 * 5) / (4 * 1) = 15/4

Otrzymaliśmy ułamek niewłaściwy. Możemy go zamienić na liczbę mieszaną:

15/4 = 3 i 3/4

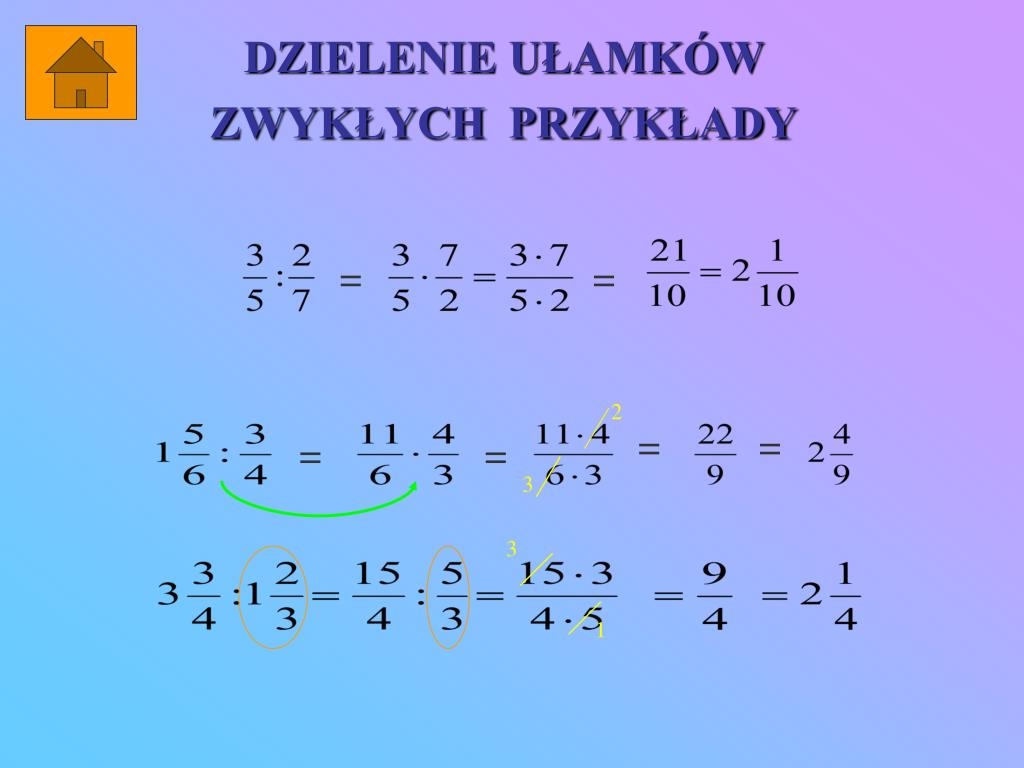
Przejdźmy teraz do dzielenia ułamków. Dzielenie ułamków to tak naprawdę mnożenie przez odwrotność drugiego ułamka. To brzmi skomplikowanie, ale w praktyce jest proste.

Załóżmy, że mamy:

1/2 : 1/3

Aby podzielić 1/2 przez 1/3, musimy znaleźć odwrotność ułamka 1/3. Odwrotność ułamka to po prostu zamiana licznika z mianownikiem. Zatem odwrotność 1/3 to 3/1.

Teraz zamiast dzielić, mnożymy przez odwrotność:

1/2 * 3/1 = (1 * 3) / (2 * 1) = 3/2

Ułamek 3/2 to ułamek niewłaściwy. Zamieniamy go na liczbę mieszaną:

3/2 = 1 i 1/2

Kolejny przykład:

2/5 : 3/4

Odwrotność ułamka 3/4 to 4/3. Zatem:

2/5 * 4/3 = (2 * 4) / (5 * 3) = 8/15

Ułamka 8/15 nie da się uprościć.

A co z dzieleniem ułamka przez liczbę całkowitą? Załóżmy, że mamy:

4/7 : 2

Liczbę całkowitą 2 traktujemy jako ułamek 2/1. Odwrotność 2/1 to 1/2. Zatem:

4/7 * 1/2 = (4 * 1) / (7 * 2) = 4/14

Upraszczamy ułamek 4/14, dzieląc licznik i mianownik przez 2:

4/14 = 2/7

Zadania Złożone

Często w zadaniach dla klasy 6 pojawiają się kombinacje mnożenia i dzielenia ułamków. W takich przypadkach należy pamiętać o kolejności wykonywania działań (kolejność działań: nawiasy, potęgowanie i pierwiastkowanie, mnożenie i dzielenie, dodawanie i odejmowanie).

Przykład:

(1/2 + 1/4) * 2/3 : 1/6

Najpierw rozwiązujemy działanie w nawiasie:

1/2 + 1/4 = 2/4 + 1/4 = 3/4

Teraz mamy:

3/4 * 2/3 : 1/6

Wykonujemy mnożenie:

3/4 * 2/3 = (3 * 2) / (4 * 3) = 6/12 = 1/2

Teraz mamy:

1/2 : 1/6

Dzielimy:

1/2 * 6/1 = (1 * 6) / (2 * 1) = 6/2 = 3

Ostateczny wynik to 3.

Inny przykład:

2/5 : (1/3 - 1/6) * 3/4

Najpierw rozwiązujemy działanie w nawiasie:

1/3 - 1/6 = 2/6 - 1/6 = 1/6

Teraz mamy:

2/5 : 1/6 * 3/4

Wykonujemy dzielenie:

2/5 * 6/1 = (2 * 6) / (5 * 1) = 12/5

Teraz mamy:

12/5 * 3/4 = (12 * 3) / (5 * 4) = 36/20

Upraszczamy ułamek 36/20, dzieląc licznik i mianownik przez 4:

36/20 = 9/5

Zamieniamy na liczbę mieszaną:

9/5 = 1 i 4/5

Praktyczne Wskazówki

Upraszczaj Ułamki Przed Mnożeniem/Dzieleniem: Jeśli to możliwe, upraszczaj ułamki przed rozpoczęciem mnożenia lub dzielenia. To ułatwi obliczenia i zmniejszy prawdopodobieństwo popełnienia błędu. Na przykład, w wyrażeniu 4/6 * 3/2, uprość 4/6 do 2/3, a następnie pomnóż.
Zamieniaj Liczby Mieszane na Ułamki Niewłaściwe: Przed mnożeniem lub dzieleniem liczb mieszanych, zamień je na ułamki niewłaściwe. Na przykład, zamiast mnożyć 2 i 1/2 * 1/3, zamień 2 i 1/2 na 5/2, a następnie pomnóż.
Pamiętaj o Kolejności Działań: Przy rozwiązywaniu zadań z wieloma działaniami, pamiętaj o kolejności wykonywania działań (nawiasy, mnożenie/dzielenie, dodawanie/odejmowanie).
Sprawdzaj Wyniki: Po każdym obliczeniu, sprawdź, czy wynik ma sens. Czy ułamek da się uprościć? Czy wynik jest rozsądny w kontekście zadania?
Ćwicz Regularnie: Mnożenie i dzielenie ułamków to umiejętność, którą można udoskonalić tylko poprzez regularne ćwiczenia. Rozwiązuj zadania z podręcznika, zeszytu ćwiczeń i dodatkowych materiałów.

Przykładowe Zadania

Oblicz: 2/7 * 5/9
Oblicz: 3/8 : 1/4
Oblicz: (1/3 + 1/6) * 4/5
Oblicz: 5/8 : (2/3 - 1/6)
Pani Kowalska kupiła 3/4 kg jabłek po 4 zł za kilogram. Ile zapłaciła?
Podziel pizzę na 8 kawałków. Zjadłeś 3/8 pizzy. Ile kawałków zjadłeś?
Zadanie z treścią: W klasie 6a jest 24 uczniów. 2/3 uczniów lubi matematykę. Ile uczniów lubi matematykę?

Rozwiązanie zadań:

2/7 * 5/9 = (2 * 5) / (7 * 9) = 10/63
3/8 : 1/4 = 3/8 * 4/1 = (3 * 4) / (8 * 1) = 12/8 = 3/2 = 1 i 1/2
(1/3 + 1/6) * 4/5 = (2/6 + 1/6) * 4/5 = 3/6 * 4/5 = 1/2 * 4/5 = (1 * 4) / (2 * 5) = 4/10 = 2/5
5/8 : (2/3 - 1/6) = 5/8 : (4/6 - 1/6) = 5/8 : 3/6 = 5/8 : 1/2 = 5/8 * 2/1 = (5 * 2) / (8 * 1) = 10/8 = 5/4 = 1 i 1/4
3/4 * 4 = 3/4 * 4/1 = (3 * 4) / (4 * 1) = 12/4 = 3 zł
3/8 * 8 = 3/8 * 8/1 = (3 * 8) / (8 * 1) = 24/8 = 3 kawałki
2/3 * 24 = 2/3 * 24/1 = (2 * 24) / (3 * 1) = 48/3 = 16 uczniów

Mam nadzieję, że ten artykuł pomoże Wam lepiej zrozumieć i rozwiązywać zadania z mnożenia i dzielenia ułamków zwykłych. Pamiętajcie o regularnych ćwiczeniach i dokładnym sprawdzaniu wyników. Powodzenia!