Mnożenie I Dzielenie Ułamków Zwykłych Zadania Klasa 6

Dobrze, oto artykuł wyjaśniający mnożenie i dzielenie ułamków zwykłych, napisany prostym językiem dla uczniów klasy 6:

Hej klaso! Dzisiaj zajmiemy się mnożeniem i dzieleniem ułamków zwykłych. To wcale nie jest takie trudne, jak się wydaje! Postaram się to wytłumaczyć jak najprościej, żebyście mogli z łatwością rozwiązywać zadania.

Mnożenie Ułamków

Mnożenie ułamków jest naprawdę proste. Po prostu mnożymy licznik z licznikiem i mianownik z mianownikiem.

Przykład 1:

Mamy ułamek 1/2 i chcemy go pomnożyć przez ułamek 2/3.

Robimy tak:

(1/2) * (2/3) = (1 * 2) / (2 * 3) = 2/6

Teraz, jeśli to możliwe, skracamy ułamek. 2/6 można skrócić przez 2, czyli dzielimy górę i dół przez 2.

2/6 = 1/3

Więc (1/2) * (2/3) = 1/3

Przykład 2:

Pomnóżmy teraz 3/4 przez 1/5.

(3/4) * (1/5) = (3 * 1) / (4 * 5) = 3/20

Ułamka 3/20 nie da się skrócić, więc to jest nasz ostateczny wynik.

Przykład 3:

A co, jeśli mamy ułamek i liczbę naturalną? Na przykład 2/5 * 3.

Pamiętajcie, że każdą liczbę naturalną możemy zapisać jako ułamek z mianownikiem 1. Czyli 3 to to samo co 3/1.

Teraz mnożymy:

(2/5) * (3/1) = (2 * 3) / (5 * 1) = 6/5

Ułamek 6/5 to ułamek niewłaściwy (licznik jest większy od mianownika). Możemy go zamienić na liczbę mieszaną. Ile razy 5 mieści się w 6? Raz, i zostaje nam 1 reszty.

Czyli 6/5 = 1 1/5 (jeden i jedna piąta).

Skracanie Przed Mnożeniem

Czasem możemy sobie ułatwić życie, skracając ułamki przed ich pomnożeniem. To znaczy, szukamy liczb, które dzielą zarówno licznik jednego ułamka, jak i mianownik drugiego ułamka.

Przykład:

Mamy pomnożyć 4/9 przez 3/8.

(4/9) * (3/8)

Zauważamy, że 4 i 8 dzielą się przez 4. Dzielimy więc 4 przez 4 (otrzymujemy 1) i 8 przez 4 (otrzymujemy 2).

Podobnie, 3 i 9 dzielą się przez 3. Dzielimy 3 przez 3 (otrzymujemy 1) i 9 przez 3 (otrzymujemy 3).

Teraz mamy:

(1/3) * (1/2) = (1 * 1) / (3 * 2) = 1/6

O wiele prościej, prawda? Gdybyśmy pomnożyli najpierw, mielibyśmy 12/72, a potem musielibyśmy to skrócić.

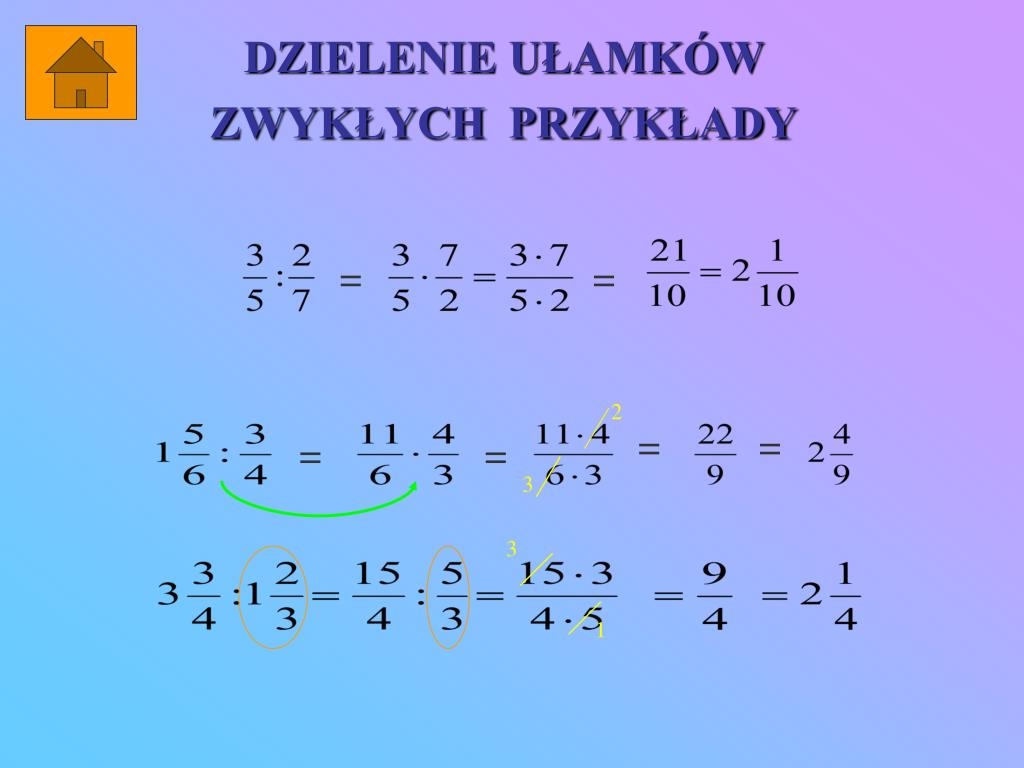
Dzielenie Ułamków

Dzielenie ułamków jest prawie tak proste jak mnożenie. Jest jeden mały haczyk: musimy odwrócić drugi ułamek i zamienić dzielenie na mnożenie.

Przykład 1:

Mamy ułamek 1/2 i chcemy go podzielić przez ułamek 1/4.

(1/2) : (1/4)

Odwracamy drugi ułamek (1/4), czyli zamieniamy licznik z mianownikiem. Otrzymujemy 4/1 (czyli po prostu 4).

Teraz zamieniamy dzielenie na mnożenie:

(1/2) * (4/1) = (1 * 4) / (2 * 1) = 4/2

Skracamy ułamek 4/2 przez 2:

4/2 = 2/1 = 2

Więc (1/2) : (1/4) = 2

Przykład 2:

Podzielmy 2/3 przez 5/6.

(2/3) : (5/6)

Odwracamy drugi ułamek: 6/5

Zamieniamy dzielenie na mnożenie:

(2/3) * (6/5) = (2 * 6) / (3 * 5) = 12/15

Skracamy ułamek 12/15 przez 3:

12/15 = 4/5

Więc (2/3) : (5/6) = 4/5

Przykład 3:

A co, jeśli dzielimy ułamek przez liczbę naturalną? Na przykład 3/7 : 2.

Pamiętamy, że 2 to to samo co 2/1.

(3/7) : (2/1)

Odwracamy drugi ułamek: 1/2

Zamieniamy dzielenie na mnożenie:

(3/7) * (1/2) = (3 * 1) / (7 * 2) = 3/14

Ułamka 3/14 nie da się skrócić.

Dzielenie i Skracanie

Podobnie jak przy mnożeniu, możemy czasem skrócić ułamki po odwróceniu drugiego ułamka i zamianie dzielenia na mnożenie.

Przykład:

Mamy podzielić 5/8 przez 15/16.

(5/8) : (15/16)

Odwracamy drugi ułamek: 16/15

Zamieniamy dzielenie na mnożenie:

(5/8) * (16/15)

Teraz możemy skrócić. 5 i 15 dzielą się przez 5. Dzielimy 5 przez 5 (otrzymujemy 1) i 15 przez 5 (otrzymujemy 3).

8 i 16 dzielą się przez 8. Dzielimy 8 przez 8 (otrzymujemy 1) i 16 przez 8 (otrzymujemy 2).

Teraz mamy:

(1/1) * (2/3) = (1 * 2) / (1 * 3) = 2/3

Więc (5/8) : (15/16) = 2/3

Kiedy Stosować Mnożenie i Dzielenie

Mnożenie ułamków stosujemy, gdy chcemy znaleźć jakąś część z innej części. Na przykład, jeśli mamy pół ciasta (1/2) i chcemy zjeść tylko ćwierć tego kawałka (1/4), to liczymy:

(1/4) * (1/2) = 1/8

Czyli zjemy 1/8 całego ciasta.

Dzielenie ułamków stosujemy, gdy chcemy podzielić coś na równe części, gdy te części są ułamkami. Na przykład, jeśli mamy 3/4 czekolady i chcemy podzielić ją równo pomiędzy 2 osoby, to liczymy:

(3/4) : 2 = (3/4) : (2/1) = (3/4) * (1/2) = 3/8

Czyli każda osoba dostanie 3/8 czekolady.

Pamiętajcie, żeby zawsze uważnie czytać zadanie i zastanowić się, czy trzeba pomnożyć, czy podzielić.

Mam nadzieję, że teraz mnożenie i dzielenie ułamków zwykłych jest dla was bardziej zrozumiałe! Ćwiczcie regularnie, rozwiązujcie zadania, a na pewno staniecie się ekspertami w tej dziedzinie. Powodzenia!