Mnożenie I Dzielenie Potęg O Tych Samych Wykładnikach

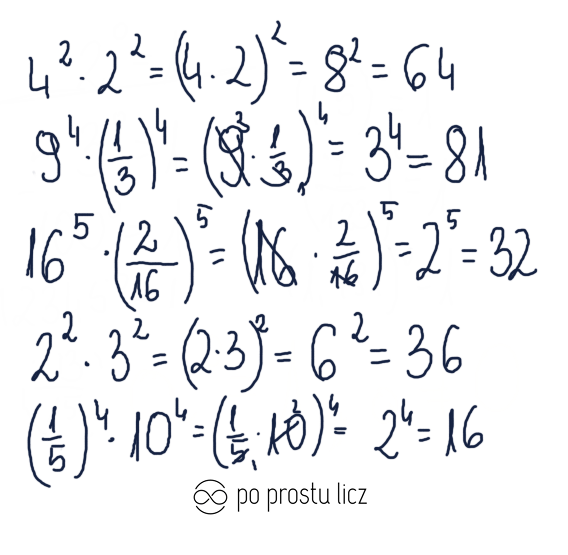
Jasne, oto artykuł tłumaczący mnożenie i dzielenie potęg o tych samych wykładnikach, napisany w prostym języku i z uwzględnieniem Twoich wskazówek:

Hej wszystkim! Dzisiaj porozmawiamy o bardzo fajnej rzeczy związanej z potęgami: mnożeniu i dzieleniu potęg, które mają ten sam wykładnik. Brzmi skomplikowanie? Spokojnie, zaraz zobaczycie, że to całkiem proste.

Mnożenie Potęg o Tych Samych Wykładnikach

Wyobraźcie sobie, że macie dwa wyrażenia, w których coś podnosicie do tej samej potęgi. Na przykład: 2³ i 3³. Widzicie? Oba są podniesione do potęgi 3.

Co zrobić, żeby to pomnożyć? To proste! Mnożymy to, co jest podnoszone do potęgi (czyli podstawy), a wykładnik zostawiamy bez zmian. Czyli w naszym przykładzie:

2³ * 3³ = (2 * 3)³ = 6³

I to wszystko! Pomnożyliśmy 2 i 3, żeby dostać 6, a wykładnik 3 został taki sam.

Spróbujmy jeszcze jednego przykładu. Załóżmy, że mamy:

5² * 4² = (5 * 4)² = 20²

Znowu, pomnożyliśmy podstawy (5 i 4) i zostawiliśmy wykładnik (2) bez zmian.

To działa zawsze, kiedy mnożymy potęgi o tych samych wykładnikach. Nieważne, czy liczby są małe, duże, czy to ułamki – zasada jest taka sama.

Na przykład:

(1/2)⁴ * 6⁴ = (1/2 * 6)⁴ = 3⁴

Pamiętajcie, że to działa tylko wtedy, gdy wykładniki są takie same! Jeśli mamy 2³ * 2², to już inna historia (wtedy dodajemy wykładniki, ale to na inną lekcję).

A co, jeśli mamy literki zamiast liczb? Też działa! Załóżmy, że mamy a⁵ * b⁵. Wtedy:

a⁵ * b⁵ = (a * b)⁵ = (ab)⁵

Czyli po prostu zapisujemy "ab" w nawiasie i podnosimy do potęgi 5.

Dzielenie Potęg o Tych Samych Wykładnikach

Teraz przejdźmy do dzielenia. To bardzo podobne do mnożenia, tylko zamiast mnożyć, dzielimy.

Załóżmy, że mamy 6³ / 3³. Co robimy? Dzielimy podstawy (6 i 3), a wykładnik zostawiamy bez zmian. Czyli:

6³ / 3³ = (6 / 3)³ = 2³

Proste, prawda? Podzieliliśmy 6 przez 3, żeby dostać 2, a wykładnik 3 został taki sam.

Inny przykład:

10² / 2² = (10 / 2)² = 5²

Podzieliliśmy 10 przez 2 i zostawiliśmy wykładnik 2.

Podobnie jak przy mnożeniu, to działa zawsze, kiedy dzielimy potęgi o tych samych wykładnikach. I tak samo, jeśli mamy ułamki, to też działa:

(9/2)⁴ / (3/2)⁴ = ((9/2) / (3/2))⁴ = (9/2 * 2/3)⁴ = (3)⁴

Pamiętajcie, że dzielenie przez ułamek to to samo, co mnożenie przez jego odwrotność. Dlatego (9/2) / (3/2) zamieniło się w (9/2 * 2/3).

A co z literkami? Dokładnie to samo! Załóżmy, że mamy a⁵ / b⁵. Wtedy:

a⁵ / b⁵ = (a / b)⁵

Czyli zapisujemy "a/b" w nawiasie i podnosimy do potęgi 5.

Ważna uwaga: Pamiętajcie, że nie możemy dzielić przez zero! Czyli w przykładzie a⁵ / b⁵, "b" nie może być zerem.

Podsumowanie i kilka dodatkowych przykładów

Żeby to wszystko utrwalić, zróbmy jeszcze kilka przykładów.

Mamy 7³ * 2³. Co robimy? Mnożymy 7 i 2, a wykładnik zostawiamy bez zmian:

7³ * 2³ = (7 * 2)³ = 14³
Mamy 15² / 5². Co robimy? Dzielimy 15 przez 5, a wykładnik zostawiamy bez zmian:

15² / 5² = (15 / 5)² = 3²
Mamy (1/3)⁵ * 9⁵. Co robimy? Mnożymy 1/3 i 9, a wykładnik zostawiamy bez zmian:

(1/3)⁵ * 9⁵ = (1/3 * 9)⁵ = 3⁵
Mamy x⁷ / y⁷. Co robimy? Dzielimy x przez y, a wykładnik zostawiamy bez zmian:

x⁷ / y⁷ = (x / y)⁷

Mam nadzieję, że teraz mnożenie i dzielenie potęg o tych samych wykładnikach jest dla Was jasne. Pamiętajcie o tej prostej zasadzie: mnożymy lub dzielimy podstawy, a wykładnik zostaje taki sam. To wszystko! Teraz możecie ćwiczyć i rozwiązywać zadania. Powodzenia!