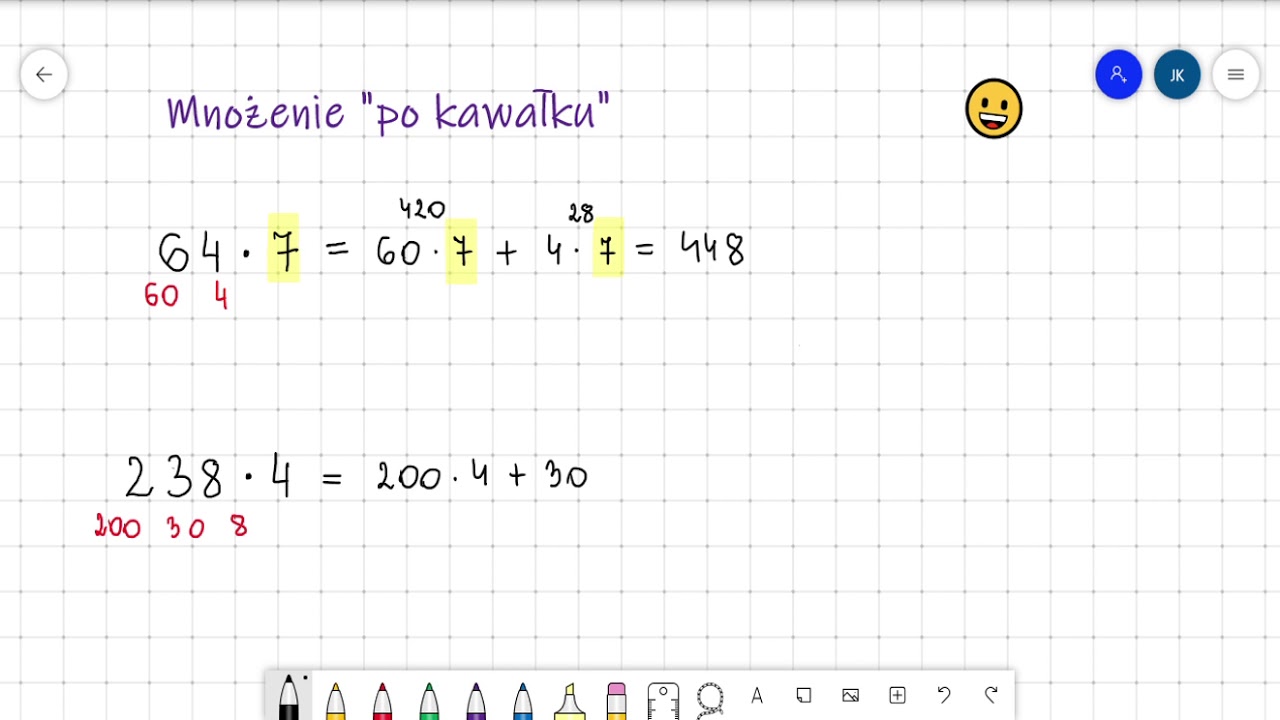Mnożenie I Dzielenie Po Kawałku

Czy kiedykolwiek patrzyłeś na skomplikowane działanie matematyczne i czułeś, że chcesz je… pociąć na mniejsze kawałki? No cóż, mamy dla ciebie dobre wieści! Istnieje metoda, która pozwala na łatwiejsze i bardziej intuicyjne rozwiązywanie zadań z mnożenia i dzielenia, szczególnie tych z większymi liczbami. Nazywa się "mnożenie i dzielenie po kawałku", a ten artykuł pokaże Ci, jak to działa i dlaczego warto to znać.

Czym jest Mnożenie i Dzielenie "Po Kawałku"?

Mnożenie i dzielenie "po kawałku", znane także jako rozkład na czynniki pierwsze lub dekompozycja, to strategia, która polega na rozbijaniu liczb na mniejsze, łatwiejsze do opanowania elementy. Zamiast próbować mnożyć 345 x 27 bezpośrednio, rozkładamy je na prostsze działania, które możemy wykonać w pamięci lub z niewielką pomocą.

Cel: Uprościć skomplikowane obliczenia poprzez dekompozycję liczb na mniejsze, bardziej zarządcze części. Dla kogo? Uczniowie, studenci, a także osoby dorosłe, które chcą poprawić swoje umiejętności obliczeniowe i poczuć się pewniej z matematyką w życiu codziennym.

Dlaczego Warto Używać Tej Metody?

Istnieje wiele powodów, dla których warto opanować mnożenie i dzielenie po kawałku:

Zwiększa zrozumienie: Zamiast mechanicznie wykonywać algorytm, rozumiesz, co się dzieje z liczbami.
Ułatwia obliczenia w pamięci: Mniejsze liczby są łatwiejsze do manipulowania w głowie.
Redukuje błędy: Rozkład na mniejsze kroki zmniejsza ryzyko pomyłek.
Poprawia intuicję matematyczną: Zauważasz wzorce i zależności, które umykają przy tradycyjnych metodach.
Zwiększa pewność siebie: Gdy opanujesz technikę, poczujesz się bardziej komfortowo z matematyką.

Mnożenie "Po Kawałku" - Krok po Kroku

Przyjrzyjmy się, jak działa mnożenie "po kawałku" na przykładzie:

Przykład: 24 x 13

Krok 1: Rozkładamy jedną z liczb (najczęściej większą) na sumę składników. W tym przypadku rozkładamy 13 na 10 + 3.

Krok 2: Wykonujemy mnożenie każdego składnika z rozkładu przez drugą liczbę (24).

24 x 10 = 240
24 x 3 = 72

Krok 3: Dodajemy wyniki cząstkowe.

240 + 72 = 312

Zatem 24 x 13 = 312

Inny Przykład: 37 x 15

Rozkładamy 15 na 10 + 5.

37 x 10 = 370
37 x 5 = (37 x 10) / 2 = 370 / 2 = 185 (Tutaj wykorzystujemy fakt, że mnożenie przez 5 jest połową mnożenia przez 10!)

Dodajemy wyniki:

370 + 185 = 555

Zatem 37 x 15 = 555

Strategie Rozkładu dla Mnożenia

Rozkład na dziesiątki i jedności: Najczęściej stosowana metoda, jak w powyższych przykładach.
Rozkład na czynniki pierwsze: Przydatne, gdy jedna z liczb ma łatwe do znalezienia czynniki pierwsze (np. 12 = 2 x 2 x 3).
Użycie liczb "okrągłych": Jeśli masz np. 19, możesz myśleć o tym jako 20 - 1.

Dzielenie "Po Kawałku" - Demistyfikacja!

Dzielenie "po kawałku" jest równie przydatne i pozwala unikać stresu związanego z długim dzieleniem pisemnym, zwłaszcza przy większych liczbach. Kluczem jest szacowanie i odejmowanie wielokrotności dzielnika.

Przykład: 252 / 6

Krok 1: Zastanawiamy się, ile razy 6 mieści się "mniej więcej" w 252. Możemy zacząć od szacowania: Czy 6 mieści się 10 razy? 6 x 10 = 60. Tak, mieści się więcej niż 10 razy.

Krok 2: Czy 6 mieści się 20 razy? 6 x 20 = 120. Tak, mieści się więcej.

Krok 3: Czy 6 mieści się 40 razy? 6 x 40 = 240. Blisko! Odejmmy 240 od 252:

252 - 240 = 12

Krok 4: Ile razy 6 mieści się w 12? 2 razy (6 x 2 = 12)

Krok 5: Dodajemy nasze "ile razy" (40 + 2 = 42)

Zatem 252 / 6 = 42

Inny Przykład: 385 / 7

Krok 1: Ile razy 7 mieści się w 385? Czy 10 razy? 7 x 10 = 70. Tak, więcej.

Krok 2: Czy 20 razy? 7 x 20 = 140. Tak, więcej.

Krok 3: Czy 50 razy? 7 x 50 = 350. Blisko!

Krok 4: 385 - 350 = 35

Krok 5: Ile razy 7 mieści się w 35? 5 razy (7 x 5 = 35)

Krok 6: 50 + 5 = 55

Zatem 385 / 7 = 55

Wskazówki do Dzielenia "Po Kawałku"

Zacznij od szacowania: Użyj liczb "okrągłych" (10, 20, 50, 100) jako punktu wyjścia.
Odejmuj stopniowo: Odejmuj wielokrotności dzielnika, aż dojdziesz do zera lub liczby mniejszej od dzielnika (reszty).
Sprawdzaj: Pomnóż wynik przez dzielnik, aby sprawdzić, czy otrzymasz pierwotną liczbę (lub liczbę z resztą dodaną).

Mnożenie i Dzielenie "Po Kawałku" w Praktyce

Gdzie możesz wykorzystać te techniki? Wszędzie tam, gdzie potrzebujesz szybko i sprawnie wykonywać obliczenia, bez użycia kalkulatora. Oto kilka przykładów:

Zakupy: Szybkie obliczanie kosztu kilku produktów o tej samej cenie.
Podróże: Szacowanie odległości i czasu podróży.
Gotowanie: Skalowanie przepisów (np. podwajanie lub potrajanie składników).
Finanse osobiste: Obliczanie rat kredytów, oprocentowania, oszczędności.
Praca: Szybkie szacowanie kosztów, zysków, produktywności.

Podsumowanie i Korzyści

Mnożenie i dzielenie "po kawałku" to potężne narzędzie, które pozwala nam zrozumieć i opanować operacje matematyczne w sposób bardziej intuicyjny. To nie tylko sposób na szybsze obliczenia, ale przede wszystkim na rozwinięcie myślenia matematycznego i pewności siebie. Zachęcamy do praktyki, eksperymentowania i odkrywania własnych strategii rozkładu liczb. Zobaczysz, jak szybko staniesz się mistrzem mnożenia i dzielenia "po kawałku"! Spróbuj już dziś, a zobaczysz różnicę!