Mnożenie I Dzielenie Liczb Całkowitych Klasa 6 Kartkówka

Rozpocznijmy przygodę z mnożeniem i dzieleniem liczb całkowitych! W klasie 6 to bardzo ważny temat, który buduje solidne fundamenty matematyczne. Przygotujmy się do kartkówki!

Zacznijmy od przypomnienia, czym są liczby całkowite. To liczby naturalne (1, 2, 3…), zero (0) oraz liczby ujemne (-1, -2, -3…). Mnożenie i dzielenie liczb całkowitych rządzi się swoimi prawami, a zrozumienie tych praw jest kluczem do sukcesu na kartkówce.

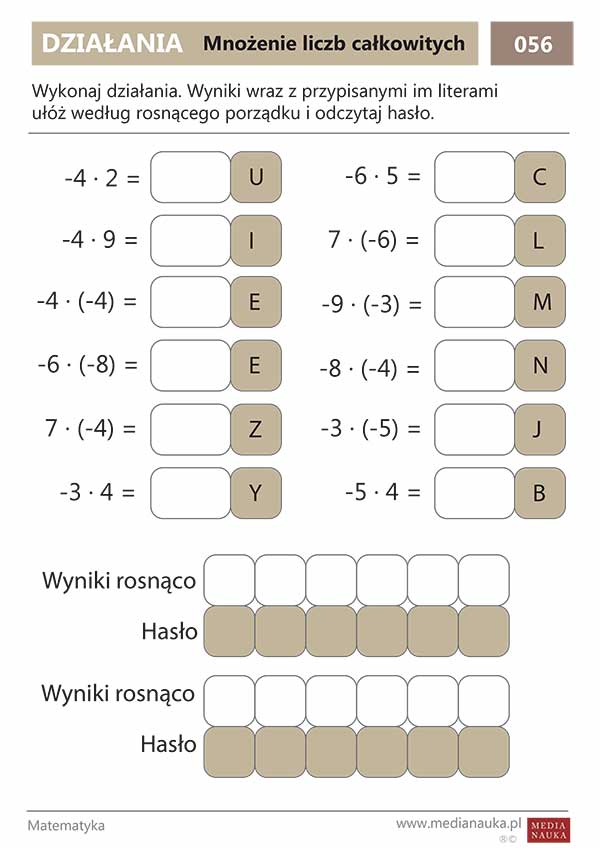
Mnożenie liczb całkowitych.

Przypomnijmy sobie, jak mnożymy liczby naturalne. Na przykład, 3 x 4 = 12. To proste! Ale co, jeśli mamy liczby ujemne?

Zasada jest taka:

• Liczba dodatnia pomnożona przez liczbę dodatnią daje liczbę dodatnią. (Np. 5 x 2 = 10)
• Liczba ujemna pomnożona przez liczbę ujemną daje liczbę dodatnią. (Np. -3 x -2 = 6)
• Liczba dodatnia pomnożona przez liczbę ujemną daje liczbę ujemną. (Np. 4 x -5 = -20)
• Liczba ujemna pomnożona przez liczbę dodatnią daje liczbę ujemną. (Np. -2 x 6 = -12)

Spójrzmy na to z innej strony. Iloczyn dwóch liczb o jednakowych znakach jest dodatni. Iloczyn dwóch liczb o różnych znakach jest ujemny.

Kilka przykładów:

• (-7) * (-3) = 21
• 8 * (-4) = -32
• (-9) * 2 = -18
• 10 * 5 = 50

Ważne jest, aby zapamiętać te zasady! Ćwiczenie czyni mistrza, więc rozwiązujmy zadania. Weźmy na przykład takie zadanie: Oblicz: (-6) * 8 * (-2).

(-6) * 8 = -48 -48 * (-2) = 96

Odp: 96

A co, jeśli mamy więcej niż dwie liczby? Mnożymy po kolei, pamiętając o znakach. Na przykład: (-2) x 3 x (-4) x (-1). Najpierw (-2) x 3 = -6. Potem -6 x (-4) = 24. Na koniec 24 x (-1) = -24. Zatem, (-2) x 3 x (-4) x (-1) = -24.

Zauważmy, że jeśli w mnożeniu występuje parzysta liczba czynników ujemnych, wynik jest dodatni. Jeśli występuje nieparzysta liczba czynników ujemnych, wynik jest ujemny. To bardzo przydatna wskazówka!

Rozwiążmy jeszcze jedno zadanie: Oblicz: (-1) * (-1) * (-1) * (-1) * (-1)

Mamy pięć czynników ujemnych, czyli nieparzystą liczbę. Zatem wynik będzie ujemny. (-1) * (-1) = 1 1 * (-1) = -1 -1 * (-1) = 1 1 * (-1) = -1

Odp: -1

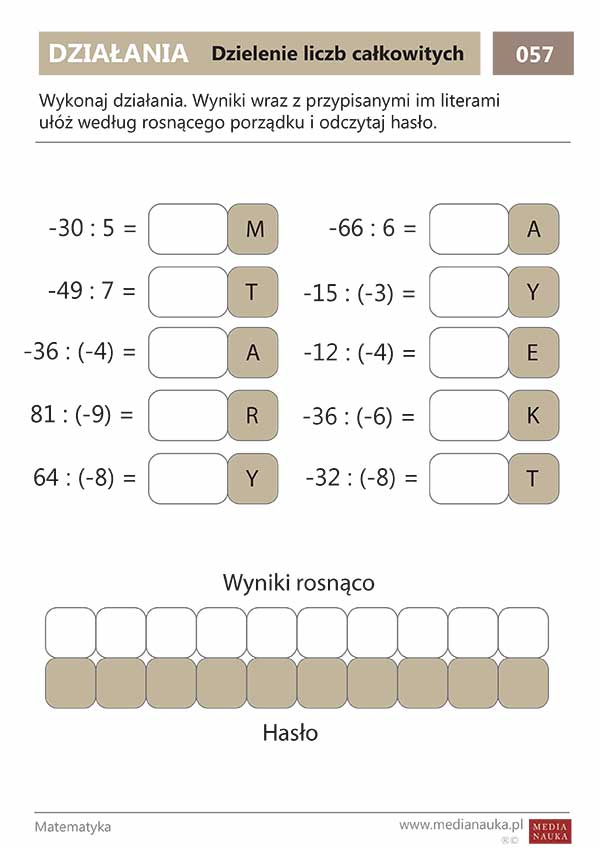
Dzielenie liczb całkowitych.

Dzielenie liczb całkowitych jest bardzo podobne do mnożenia, jeśli chodzi o zasady znaków.

• Liczba dodatnia podzielona przez liczbę dodatnią daje liczbę dodatnią. (Np. 10 / 2 = 5)
• Liczba ujemna podzielona przez liczbę ujemną daje liczbę dodatnią. (Np. -6 / -3 = 2)
• Liczba dodatnia podzielona przez liczbę ujemną daje liczbę ujemną. (Np. 20 / -5 = -4)
• Liczba ujemna podzielona przez liczbę dodatnią daje liczbę ujemną. (Np. -12 / 6 = -2)

Podobnie jak w mnożeniu: iloraz dwóch liczb o jednakowych znakach jest dodatni. Iloraz dwóch liczb o różnych znakach jest ujemny.

Kilka przykładów:

• (-15) / (-3) = 5
• 24 / (-4) = -6
• (-36) / 9 = -4
• 40 / 5 = 8

Pamiętajmy, że dzielenie przez zero jest niedozwolone! Nie możemy dzielić żadnej liczby przez zero.

Rozwiążmy zadanie: Oblicz: (-48) / 6

(-48) / 6 = -8

Odp: -8

A teraz trudniejsze zadanie: Oblicz: 72 / (-9) / (-2)

Najpierw 72 / (-9) = -8 Potem -8 / (-2) = 4

Odp: 4

Kolejne zadanie: Oblicz: (-100) / 5 / (-4)

(-100) / 5 = -20 -20 / (-4) = 5

Odp: 5

Mnożenie i dzielenie – zadania łączone.

Często na kartkówce pojawiają się zadania, w których trzeba połączyć mnożenie i dzielenie. W takich przypadkach pamiętamy o kolejności wykonywania działań: najpierw mnożenie i dzielenie (od lewej do prawej), a potem dodawanie i odejmowanie.

Przykład: Oblicz: 5 x (-3) + 12 / (-2)

Najpierw mnożenie: 5 x (-3) = -15 Potem dzielenie: 12 / (-2) = -6 Na koniec dodawanie: -15 + (-6) = -21

Odp: -21

Spróbujmy rozwiązać kolejne zadanie: (-4) * 3 - 18 / (-6)

(-4) * 3 = -12 18 / (-6) = -3 -12 - (-3) = -12 + 3 = -9

Odp: -9

I jeszcze jedno zadanie: 24 / (-3) + (-2) * 5

24 / (-3) = -8 (-2) * 5 = -10 -8 + (-10) = -18

Odp: -18

Wyrażenia Arytmetyczne z Liczbami Całkowitymi

Na kartkówce mogą pojawić się bardziej złożone wyrażenia arytmetyczne, zawierające nawiasy. Pamiętamy, że najpierw wykonujemy działania w nawiasach.

Przykład: Oblicz: (-2 + 5) x (8 - 10)

Najpierw nawiasy: -2 + 5 = 3 8 - 10 = -2 Potem mnożenie: 3 x (-2) = -6

Odp: -6

Kolejne zadanie: 15 / (3 - 8) + (-4) * (2 + 1)

Najpierw nawiasy: 3 - 8 = -5 2 + 1 = 3 Potem dzielenie i mnożenie: 15 / (-5) = -3 (-4) * 3 = -12 Na koniec dodawanie: -3 + (-12) = -15

Odp: -15

Jeszcze jedno: (-6) * (4 - 7) - 20 / (-2 - 3)

Nawiasy: 4 - 7 = -3 -2 - 3 = -5 Mnożenie i dzielenie: (-6) * (-3) = 18 20 / (-5) = -4 Odejmowanie: 18 - (-4) = 18 + 4 = 22

Odp: 22

Rozwiązywanie równań z liczbami całkowitymi

Czasami na kartkówce pojawiają się proste równania z liczbami całkowitymi. Rozwiązanie równania polega na znalezieniu takiej wartości niewiadomej (zazwyczaj oznaczanej literą x), która spełnia równanie.

Przykład: Rozwiąż równanie: x + 5 = 2

Chcemy, aby po jednej stronie równania został tylko x. W tym celu odejmujemy 5 od obu stron równania: x + 5 - 5 = 2 - 5 x = -3

Odp: x = -3

Sprawdzenie: (-3) + 5 = 2 (zgadza się!)

Kolejne równanie: x - 3 = -7

Dodajemy 3 do obu stron równania: x - 3 + 3 = -7 + 3 x = -4

Odp: x = -4

Sprawdzenie: (-4) - 3 = -7 (zgadza się!)

Równanie z mnożeniem: 2x = -10

Dzielimy obie strony równania przez 2: 2x / 2 = -10 / 2 x = -5

Odp: x = -5

Sprawdzenie: 2 * (-5) = -10 (zgadza się!)

Równanie z dzieleniem: x / (-3) = 4

Mnożymy obie strony równania przez (-3): x / (-3) * (-3) = 4 * (-3) x = -12

Odp: x = -12

Sprawdzenie: (-12) / (-3) = 4 (zgadza się!)

Pamiętajmy o sprawdzaniu rozwiązań równań! To bardzo ważne, aby upewnić się, że znaleźliśmy prawidłową wartość niewiadomej.

Zadania tekstowe z liczbami całkowitymi

Zadania tekstowe często sprawiają uczniom trudność. Kluczem do sukcesu jest uważne przeczytanie zadania i zrozumienie, o co pytają. Następnie trzeba przełożyć treść zadania na język matematyki, czyli ułożyć odpowiednie działanie lub równanie.

Przykład: Temperatura powietrza o godzinie 6:00 wynosiła -3°C. Do godziny 12:00 temperatura wzrosła o 7°C. Jaka była temperatura o godzinie 12:00?

Rozwiązanie: Początkowa temperatura: -3°C Wzrost temperatury: 7°C Temperatura o 12:00: -3 + 7 = 4°C

Odp: Temperatura o godzinie 12:00 wynosiła 4°C.

Kolejne zadanie: Dług Marysi wynosi 15 zł. Mama dała jej 8 zł. Ile teraz wynosi dług Marysi?

Rozwiązanie: Początkowy dług: -15 zł Kwota otrzymana od mamy: 8 zł Aktualny dług: -15 + 8 = -7 zł

Odp: Dług Marysi wynosi teraz 7 zł.

Pamiętaj o analizie zadania, zanim zaczniesz liczyć. Określ, co jest dane, a co masz obliczyć.

Powodzenia na kartkówce! Powtarzaj zasady, rozwiązuj zadania i nie daj się zaskoczyć!