Miary Kątów W Trapezie Równoramiennym

Drodzy Nauczyciele Matematyki,

Ten artykuł ma na celu ułatwienie Państwu nauczania o miarach kątów w trapezie równoramiennym. Omówimy kluczowe własności, typowe błędy uczniów oraz metody, które mogą uczynić ten temat bardziej przystępnym i interesującym dla uczniów.

Kluczowe Własności Trapezu Równoramiennego

Zacznijmy od definicji: Trapez równoramienny to trapez, którego ramiona są równej długości. Oznacza to, że kąty przy każdej podstawie są równe.

Główne własności, które należy podkreślić w trakcie lekcji:

Kąty przy tej samej podstawie są równe. Jeśli mamy trapez ABCD, gdzie AB jest podstawą dłuższą, a CD podstawą krótszą, to kąt DAB = kąt CBA oraz kąt ADC = kąt BCD.
Suma miar kątów przy każdym ramieniu wynosi 180 stopni. Czyli kąt DAB + kąt ADC = 180 stopni oraz kąt CBA + kąt BCD = 180 stopni. Wynika to z faktu, że ramiona tworzą z podstawami kąty wewnętrzne jednostronne, a te są suplementarne.
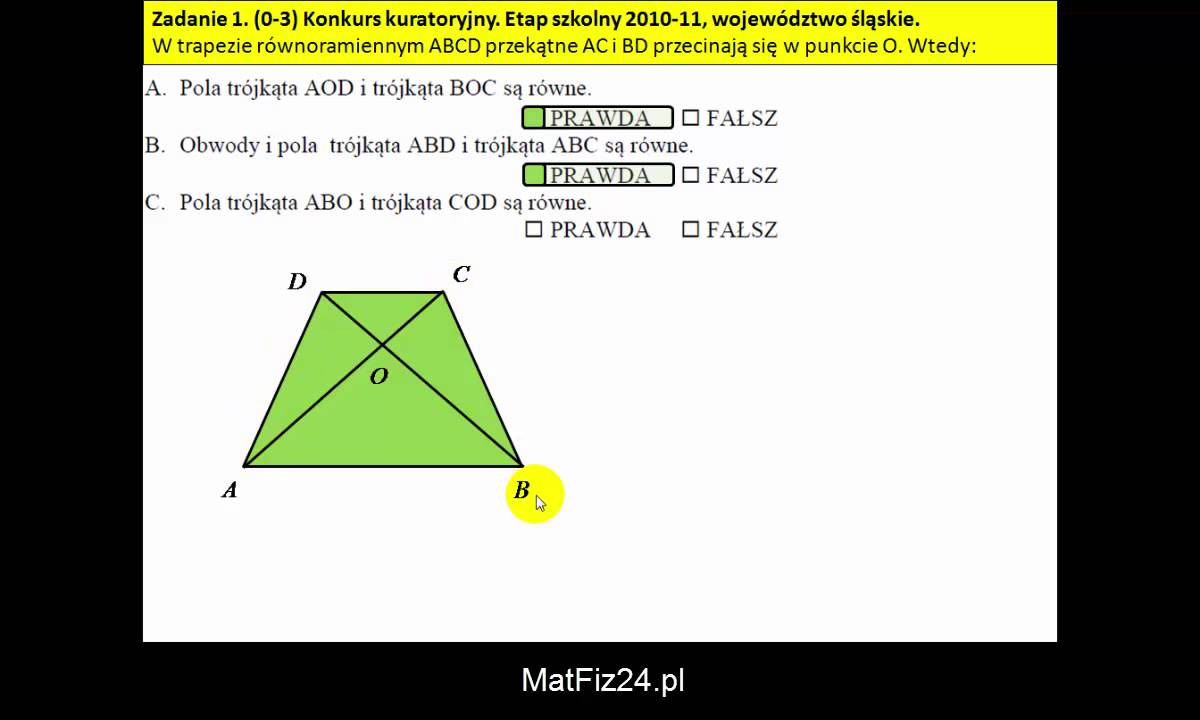
Przekątne trapezu równoramiennego są równej długości. Choć ta własność nie jest bezpośrednio związana z miarami kątów, warto ją wspomnieć, aby pokazać uczniom bogactwo własności tej figury.

Jak Efektywnie Tłumaczyć?

Oto kilka sugestii, jak skutecznie wprowadzić ten temat:

Wizualizacja: Używajcie rysunków, modeli trapezu równoramiennego. Najlepiej, aby uczniowie sami je narysowali. Pozwólcie im mierzyć kąty za pomocą kątomierza, aby sami empirycznie przekonali się o własnościach.
Podział na prostsze figury: Pokażcie, jak trapez równoramienny można rozłożyć na prostokąt i dwa trójkąty prostokątne (przystające). Pozwoli to uczniom zrozumieć związek między kątami w trapezie a kątami w znanych im już figurach.
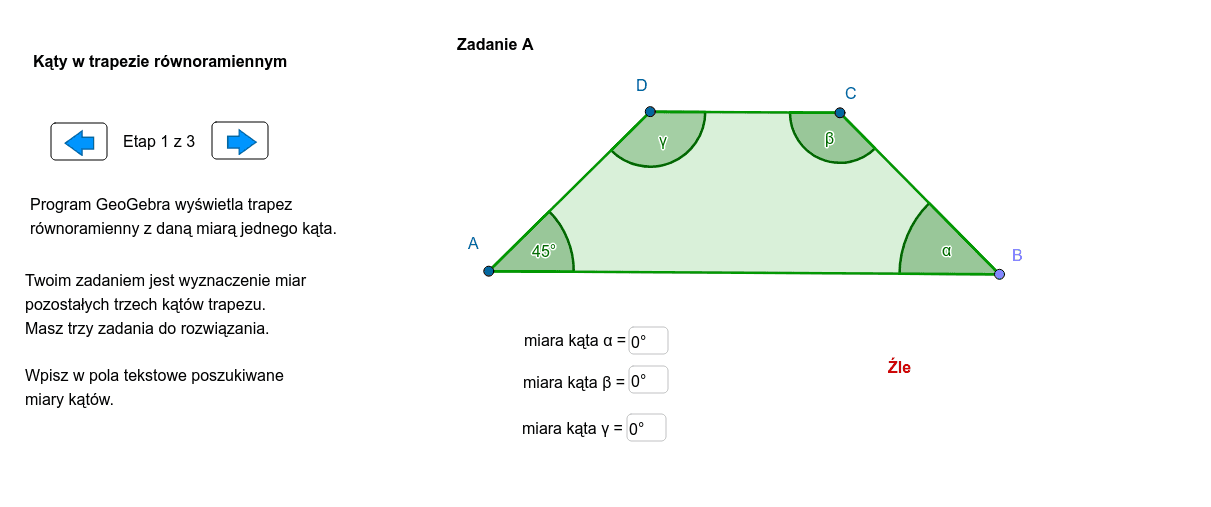
Zadania o różnym stopniu trudności: Zacznijcie od prostych zadań, gdzie podana jest miara jednego kąta, a uczniowie mają obliczyć pozostałe. Stopniowo wprowadzajcie zadania, które wymagają użycia dodatkowej wiedzy (np. związki między kątami w trójkącie).
Użycie oprogramowania geometrycznego: Programy takie jak GeoGebra pozwalają na dynamiczne manipulowanie trapezem równoramiennym i obserwowanie, jak zmieniają się miary kątów przy zmianie długości podstaw i ramion.

Typowe Błędy i Jak Im Zapobiegać

Uczniowie często popełniają następujące błędy:

Zakładają, że wszystkie kąty w trapezie równoramiennym są równe. Należy wyraźnie podkreślić, że tylko kąty przy tej samej podstawie są równe.
Nie pamiętają, że suma miar kątów przy ramieniu wynosi 180 stopni. Pomocne może być przypomnienie o kątach wewnętrznych jednostronnych, które powstają przy przecięciu dwóch prostych równoległych trzecią prostą.
Mylą trapez równoramienny z innym typem trapezu (np. prostokątnym) lub z równoległobokiem. Ważne jest, aby dobrze utrwalić definicję i własności trapezu równoramiennego.
Nie potrafią poprawnie zinterpretować danych w zadaniu. Na przykład, jeśli zadanie mówi, że kąt przy podstawie ma miarę 60 stopni, uczeń może nie wiedzieć, który kąt dokładnie chodzi. Należy ćwiczyć czytanie ze zrozumieniem i analizę rysunków.

Jak zapobiegać tym błędom?

Kładźcie nacisk na definicje i własności. Powtarzajcie je regularnie, zadawajcie pytania sprawdzające zrozumienie.
Ćwiczcie rozwiązywanie zadań. Im więcej zadań uczniowie rozwiążą, tym lepiej zrozumieją temat.
Zachęcajcie do rysowania i oznaczania rysunków. Poprawne oznaczenie kątów i boków na rysunku ułatwia rozwiązanie zadania.
Analizujcie błędy. Kiedy uczeń popełni błąd, nie karzcie go za to, ale wspólnie przeanalizujcie, gdzie popełnił błąd i dlaczego.

Angażujące Metody Nauczania

Oto kilka pomysłów, jak uatrakcyjnić lekcje o trapezie równoramiennym:

Gry i zabawy: Stwórzcie grę, w której uczniowie muszą odgadywać miary kątów w trapezie równoramiennym na podstawie podanych informacji. Można wykorzystać karty z rysunkami trapezów i zadaniami.
Praca w grupach: Podzielcie uczniów na grupy i dajcie im zadanie, np. zaprojektowanie mozaiki z trapezów równoramiennych.
Wykorzystanie kontekstu realnego: Znajdźcie przykłady trapezów równoramiennych w otoczeniu (np. w architekturze, w meblach). Pokażcie zdjęcia i zapytajcie uczniów, gdzie widzą trapezy i jakie mają własności.
Projekty: Zaproponujcie uczniom wykonanie projektu, np. zbudowanie modelu trapezu równoramiennego z kartonu lub innych materiałów.

Przykład zadania angażującego:

Wyobraź sobie, że jesteś architektem i projektujesz witraż w kształcie trapezu równoramiennego. Kąt przy jednej z podstaw ma miarę 70 stopni. Jakie miary będą miały pozostałe kąty? Wykonaj szkic witrażu, oznaczając miary wszystkich kątów.

Takie zadanie pozwala uczniom poczuć, że wiedza o trapezie równoramiennym ma praktyczne zastosowanie.

Pamiętajcie, że kluczem do sukcesu jest cierpliwość i indywidualne podejście do każdego ucznia. Starajcie się tworzyć atmosferę, w której uczniowie nie boją się zadawać pytań i popełniać błędów. Zrozumienie własności trapezu równoramiennego to ważny krok w dalszej edukacji matematycznej.

Życzymy Państwu owocnych lekcji!