Miara Kąta Wewnętrznego Sześciokąta Foremnego Jest Równa

Zastanawiasz się, jaka jest miara kąta wewnętrznego sześciokąta foremnego? Przygotuj się na podróż, która krok po kroku rozwieje Twoje wątpliwości i zapewni pełne zrozumienie tego zagadnienia.

Rozpocznijmy od definicji. Sześciokąt foremny to figura geometryczna, która posiada sześć równych boków i sześć równych kątów wewnętrznych. Słowo "foremny" jest tutaj kluczowe, ponieważ odnosi się do regularności figury. Gdybyśmy mieli do czynienia ze zwykłym sześciokątem (czyli takim, który nie musi mieć równych boków i kątów), miara kątów wewnętrznych mogłaby być różna w każdym wierzchołku.

Żeby wyznaczyć miarę kąta wewnętrznego sześciokąta foremnego, najpierw potrzebujemy znać sumę wszystkich jego kątów wewnętrznych. Wykorzystamy do tego prosty wzór, który obowiązuje dla wszystkich wielokątów. Wzór ten brzmi: (n - 2) * 180°, gdzie 'n' oznacza liczbę boków wielokąta.

W naszym przypadku n = 6, ponieważ mamy do czynienia z sześciokątem. Podstawiając tę wartość do wzoru, otrzymujemy:

(6 - 2) * 180° = 4 * 180° = 720°

To oznacza, że suma wszystkich kątów wewnętrznych sześciokąta foremnego wynosi 720 stopni.

Dzielimy i Zwyciężamy!

Teraz, kiedy znamy sumę wszystkich kątów, możemy obliczyć miarę pojedynczego kąta wewnętrznego. Ponieważ sześciokąt jest foremny, wszystkie jego kąty są równe. Wystarczy więc podzielić sumę kątów przez liczbę kątów (która jest równa liczbie boków).

Czyli: 720° / 6 = 120°

Otrzymujemy wynik 120 stopni. To jest właśnie miara jednego kąta wewnętrznego sześciokąta foremnego.

Aby lepiej to zrozumieć, wyobraź sobie sześciokąt foremny narysowany na kartce papieru. Każdy z jego sześciu kątów "otwiera się" pod kątem 120 stopni. Możesz to sprawdzić przy użyciu kątomierza, oczywiście rysując sześciokąt foremny z należytą precyzją.

Ta wiedza znajduje zastosowanie w wielu dziedzinach, od geometrii i matematyki, po architekturę i projektowanie. Sześciokąty foremne, ze względu na swoje regularne kształty i efektywne wykorzystanie przestrzeni, są często spotykane w naturze (na przykład w plastrach miodu) oraz w konstrukcjach tworzonych przez człowieka.

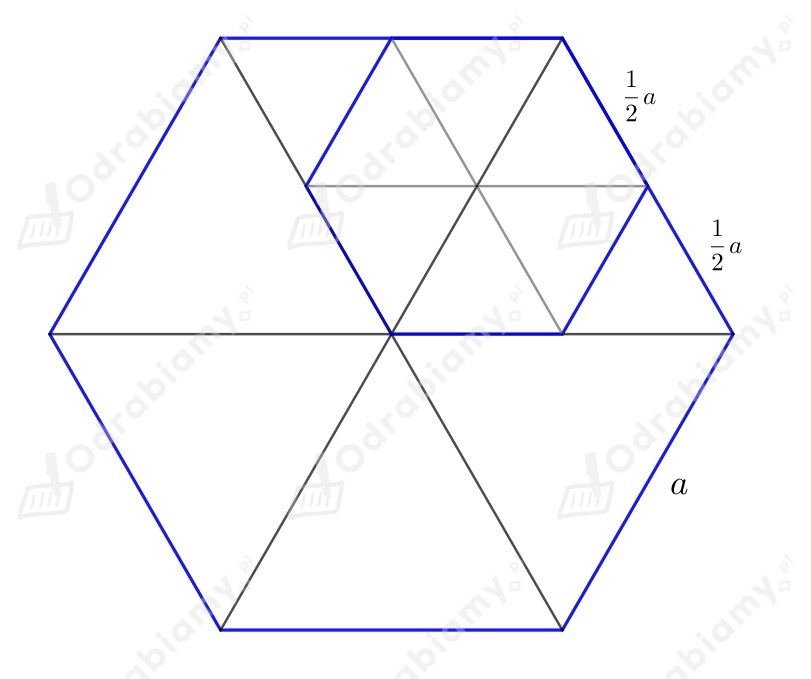
Możemy również spróbować podejść do tego problemu w inny sposób, dzieląc sześciokąt foremny na mniejsze, łatwiejsze do analizy figury. Wyobraźmy sobie, że rysujemy linie od środka sześciokąta do każdego z jego wierzchołków. W ten sposób dzielimy sześciokąt na sześć identycznych trójkątów równobocznych.

W trójkącie równobocznym każdy kąt ma miarę 60 stopni. Zauważmy, że kąt wewnętrzny sześciokąta foremnego składa się z dwóch kątów trójkąta równobocznego, które stykają się w danym wierzchołku sześciokąta.

Czyli: 60° + 60° = 120°

Ponownie, dochodzimy do tego samego wyniku: miara kąta wewnętrznego sześciokąta foremnego wynosi 120 stopni. Ta metoda, choć bardziej wizualna, potwierdza nasze wcześniejsze obliczenia i daje dodatkowe zrozumienie struktury sześciokąta foremnego.

Pamiętaj, że kluczem do zrozumienia geometrii jest praktyka. Narysuj kilka sześciokątów foremnych, zmierz ich kąty i sprawdź, czy wynik zawsze wynosi 120 stopni. Im więcej ćwiczysz, tym lepiej zrozumiesz zasady rządzące światem figur geometrycznych.

Zastosowania w Praktyce

Sześciokąty foremne, jak już wspomniałem, znajdują szerokie zastosowanie w praktyce. Ich obecność w naturze, na przykład w strukturze plastrów miodu, jest fascynująca. Pszczoły budują komórki w kształcie sześciokątów, ponieważ taki kształt pozwala na maksymalne wykorzystanie przestrzeni i minimalizację zużycia wosku. Dzięki temu, konstrukcja jest stabilna i efektywna.

W architekturze, sześciokąty foremne mogą być wykorzystywane do projektowania podłóg, ścian, a nawet całych budynków. Ich regularny kształt i możliwość łączenia w moduły pozwalają na tworzenie estetycznych i funkcjonalnych rozwiązań.

W grafice komputerowej i projektowaniu gier, sześciokąty foremne są często używane do tworzenia map i środowisk. Pozwalają na łatwe dzielenie przestrzeni i implementację ruchu postaci w grze.

Nawet w chemii, sześciokąty foremne są obecne w strukturach molekularnych. Na przykład, pierścień benzenu, który jest podstawowym elementem wielu związków organicznych, ma kształt sześciokąta foremnego.

Dlatego też, zrozumienie właściwości sześciokąta foremnego, w tym miary jego kątów wewnętrznych, jest cenną umiejętnością, która może przydać się w wielu różnych dziedzinach.

Podsumowując, miara kąta wewnętrznego sześciokąta foremnego wynosi 120 stopni. Do obliczenia tej wartości wykorzystaliśmy wzór na sumę kątów wewnętrznych wielokąta oraz podzieliliśmy otrzymaną sumę przez liczbę kątów sześciokąta. Dodatkowo, analizowaliśmy strukturę sześciokąta, dzieląc go na trójkąty równoboczne, co potwierdziło nasz wynik. Pamiętaj, że praktyka i zrozumienie podstawowych zasad geometrii są kluczowe do opanowania tej wiedzy. Powodzenia!