Matematyka Pola Figur Klasa 5
Hej! Zastanawiasz się, jak obliczyć pole różnych kształtów? Ten artykuł jest dla Ciebie! Skierowany jest do uczniów klasy 5, którzy dopiero zaczynają swoją przygodę z geometrią. Razem odkryjemy tajniki obliczania pól figur, a dzięki temu matematyka stanie się jeszcze bardziej zrozumiała i ciekawa!
Wprowadzenie do Pola Figur
Wyobraź sobie, że malujesz płot. Musisz wiedzieć, ile farby potrzebujesz, prawda? Obliczenie pola pomoże Ci to ustalić! Pole figury to po prostu miara powierzchni, jaką ta figura zajmuje. Mówiąc prościej, to ile "miejsca" jest wewnątrz danej figury.
Do obliczania pola używamy różnych jednostek. Najczęściej spotykane to:
- centymetry kwadratowe (cm²) – wyobraź sobie kwadrat o boku 1 cm, jego pole to 1 cm²
- metry kwadratowe (m²) – kwadrat o boku 1 m ma pole 1 m²
- kilometry kwadratowe (km²) – używane do mierzenia bardzo dużych obszarów, np. powierzchni miast czy krajów
Dlaczego Pole Figur Jest Ważne?
Pomyślmy o praktycznych zastosowaniach! Obliczanie pola jest niezwykle przydatne w życiu codziennym. Na przykład:
- Podczas remontu – obliczamy pole ścian, podłogi, aby kupić odpowiednią ilość farby, płytek, paneli.
- W ogrodnictwie – obliczamy powierzchnię rabaty, aby wiedzieć, ile nasion wysiać.
- W rolnictwie – rolnicy obliczają powierzchnię pól, aby wiedzieć, ile nawozu potrzebują.
- W architekturze – architekci obliczają powierzchnię pomieszczeń, aby zaprojektować budynki.
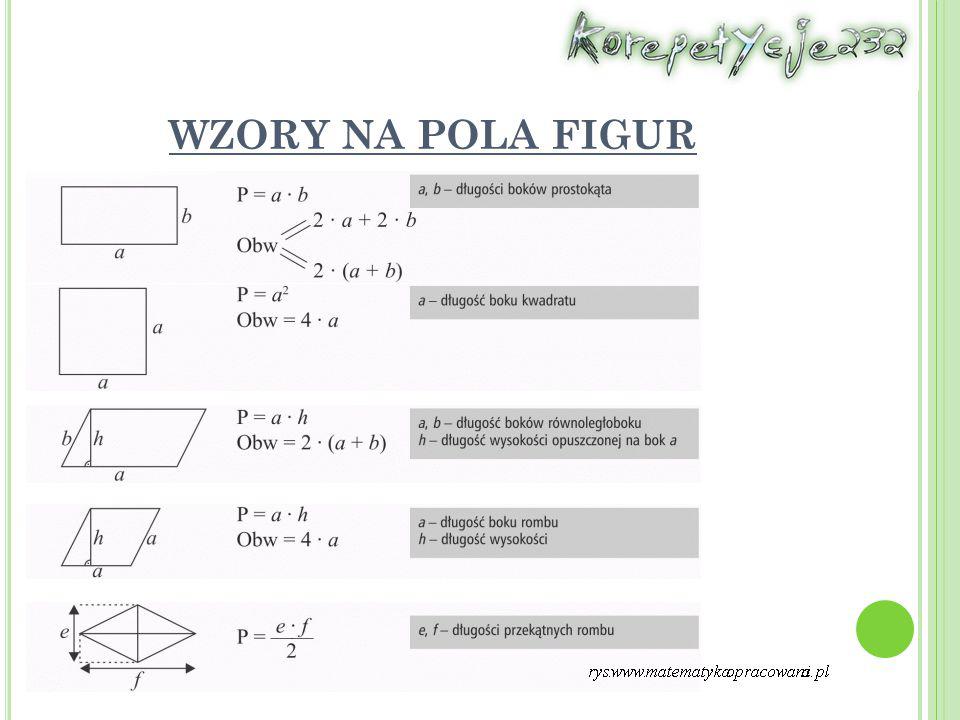
Obliczanie Pola Prostokąta i Kwadratu
Zaczynamy od najprostszych figur: prostokąta i kwadratu. To świetne figury na początek, ponieważ ich pole oblicza się bardzo łatwo!
Pole Prostokąta
Prostokąt ma dwa boki krótsze (szerokość) i dwa boki dłuższe (długość). Aby obliczyć jego pole, wystarczy pomnożyć długość przez szerokość:
Pole prostokąta = długość * szerokość (czyli P = a * b)
Przykład:
Wyobraź sobie prostokąt o długości 5 cm i szerokości 3 cm. Jego pole wynosi:
P = 5 cm * 3 cm = 15 cm²
Zatem, pole tego prostokąta to 15 centymetrów kwadratowych.
Pole Kwadratu
Kwadrat to szczególny rodzaj prostokąta, w którym wszystkie boki są równe. Zatem, aby obliczyć pole kwadratu, wystarczy pomnożyć długość boku przez siebie:
Pole kwadratu = bok * bok (czyli P = a * a, inaczej P = a²)
Przykład:
Wyobraź sobie kwadrat o boku 4 cm. Jego pole wynosi:
P = 4 cm * 4 cm = 16 cm²
Zatem, pole tego kwadratu to 16 centymetrów kwadratowych.
Obliczanie Pola Równoległoboku
Równoległobok to figura, która ma dwie pary boków równoległych. Nie wszystkie kąty są proste, jak w prostokącie, ale zasada obliczania pola jest bardzo podobna!
Aby obliczyć pole równoległoboku, potrzebujemy znać długość jego podstawy (a) i wysokość (h) opuszczoną na tę podstawę. Wysokość to odcinek prostopadły do podstawy, łączący ją z przeciwległym bokiem.
Pole równoległoboku = podstawa * wysokość (czyli P = a * h)
Przykład:
Wyobraź sobie równoległobok o podstawie 6 cm i wysokości 4 cm. Jego pole wynosi:
P = 6 cm * 4 cm = 24 cm²
Zatem, pole tego równoległoboku to 24 centymetry kwadratowe.
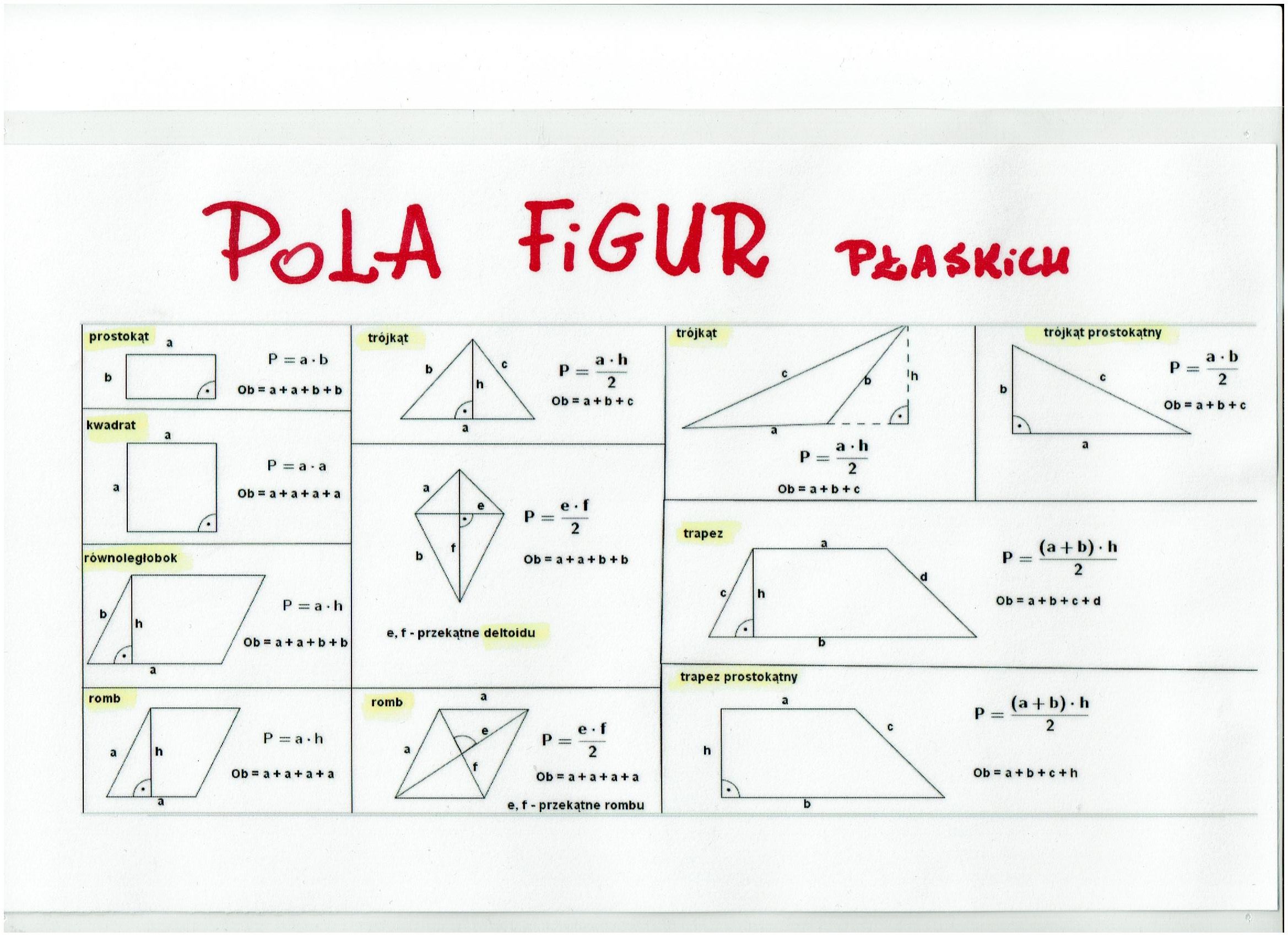
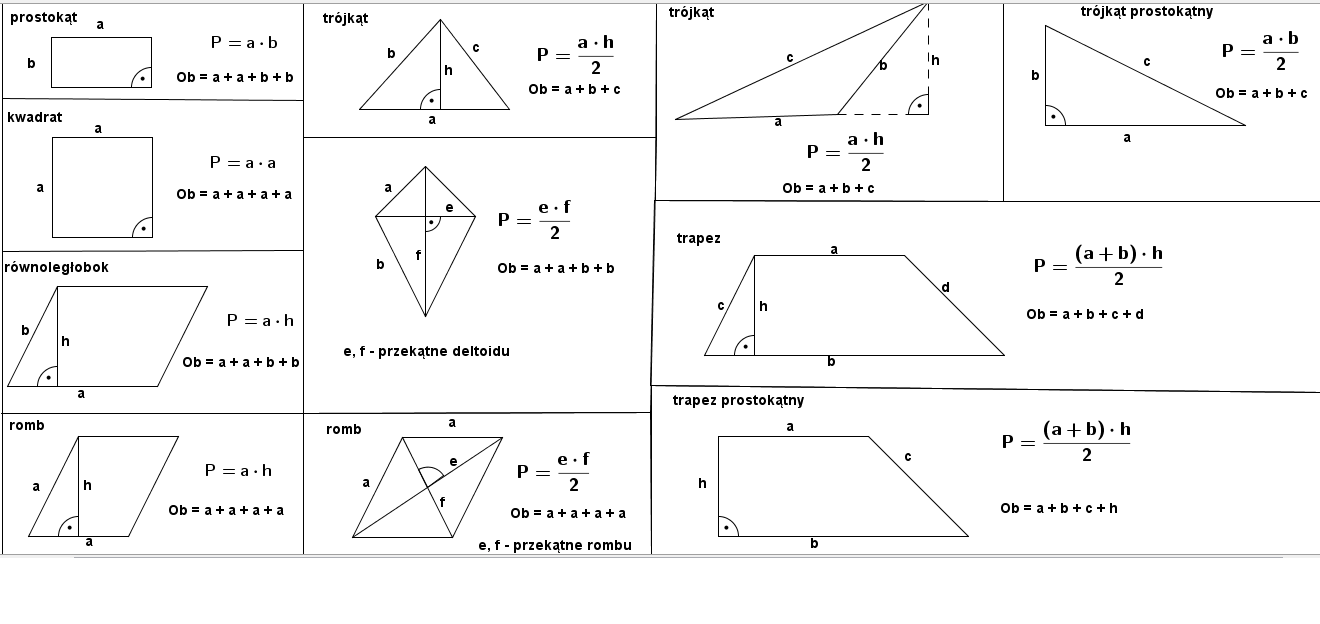
Obliczanie Pola Trójkąta
Trójkąt to figura, która ma trzy boki i trzy kąty. Obliczanie jego pola jest trochę inne niż w przypadku prostokąta czy równoległoboku.
Podobnie jak w równoległoboku, potrzebujemy znać długość podstawy (a) i wysokość (h) opuszczoną na tę podstawę. Wysokość to odcinek prostopadły do podstawy, łączący ją z przeciwległym wierzchołkiem.
Pole trójkąta = (podstawa * wysokość) / 2 (czyli P = (a * h) / 2)
Dlaczego dzielimy przez 2? Można sobie wyobrazić, że trójkąt to połowa równoległoboku.
Przykład:
Wyobraź sobie trójkąt o podstawie 8 cm i wysokości 5 cm. Jego pole wynosi:
P = (8 cm * 5 cm) / 2 = 40 cm² / 2 = 20 cm²
Zatem, pole tego trójkąta to 20 centymetrów kwadratowych.
Obliczanie Pola Rombu
Romb to czworokąt, który ma wszystkie boki równe. Jego przekątne przecinają się pod kątem prostym.
Aby obliczyć pole rombu, możemy użyć dwóch sposobów:
- Znając długość boku (a) i wysokość (h) opuszczoną na ten bok:
- Znając długości przekątnych (e i f):
Pole rombu = bok * wysokość (czyli P = a * h)
Pole rombu = (przekątna e * przekątna f) / 2 (czyli P = (e * f) / 2)
Przykład (przekątne):
Wyobraź sobie romb, którego przekątne mają długości 6 cm i 8 cm. Jego pole wynosi:
P = (6 cm * 8 cm) / 2 = 48 cm² / 2 = 24 cm²
Zatem, pole tego rombu to 24 centymetry kwadratowe.
Obliczanie Pola Trapezu
Trapez to czworokąt, który ma co najmniej jedną parę boków równoległych. Te boki nazywamy podstawami (a i b). Potrzebujemy także znać wysokość (h) trapezu, czyli odległość między podstawami.
Pole trapezu = ((podstawa a + podstawa b) * wysokość) / 2 (czyli P = ((a + b) * h) / 2)
Przykład:
Wyobraź sobie trapez o podstawach długości 5 cm i 7 cm oraz wysokości 4 cm. Jego pole wynosi:
P = ((5 cm + 7 cm) * 4 cm) / 2 = (12 cm * 4 cm) / 2 = 48 cm² / 2 = 24 cm²
Zatem, pole tego trapezu to 24 centymetry kwadratowe.
Ćwiczenia i Przykłady
Czas na praktykę! Spróbuj rozwiązać kilka zadań:
- Oblicz pole prostokąta o długości 7 cm i szerokości 2 cm.
- Oblicz pole kwadratu o boku 6 cm.
- Oblicz pole równoległoboku o podstawie 10 cm i wysokości 3 cm.
- Oblicz pole trójkąta o podstawie 9 cm i wysokości 4 cm.
- Oblicz pole rombu, którego przekątne mają długości 5 cm i 10 cm.
- Oblicz pole trapezu o podstawach długości 4 cm i 6 cm oraz wysokości 5 cm.
Spróbuj również poszukać w swoim otoczeniu różnych przedmiotów i obliczyć ich pole. Na przykład, zmierz zeszyt, książkę, stół i oblicz ich powierzchnię!
Podsumowanie
Gratulacje! Właśnie poznałeś/poznałaś podstawy obliczania pól figur. Pamiętaj, że praktyka czyni mistrza, więc im więcej ćwiczysz, tym łatwiej będzie Ci obliczać pola różnych kształtów. Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, czym jest pole figury i jak je obliczać. Teraz możesz śmiało ruszać na podbój świata geometrii! Powodzenia! Matematyka wcale nie musi być trudna!