Matematyka Klasa 6 Mnożenie I Dzielenie Liczb Całkowitych

Mnożenie i dzielenie liczb całkowitych to fundament, na którym budowana jest dalsza wiedza matematyczna. W klasie 6. uczniowie zaczynają zgłębiać te operacje, a zrozumienie ich zasad jest kluczowe dla sukcesu w przyszłych zagadnieniach. Zapraszam do podróży po świecie mnożenia i dzielenia liczb całkowitych!

Na początek, przypomnijmy sobie, czym w ogóle są liczby całkowite. Obejmują one liczby naturalne (1, 2, 3...), zero (0) oraz liczby ujemne (-1, -2, -3...). Mnożąc lub dzieląc liczby całkowite, musimy pamiętać o zasadach znaków.

Mnożenie liczb całkowitych

Zacznijmy od mnożenia. Mnożenie to w gruncie rzeczy skrócony zapis dodawania. Na przykład, 3 * 4 to to samo co 4 + 4 + 4. Ale co się dzieje, gdy w grę wchodzą liczby ujemne? Tutaj kluczowe są zasady dotyczące znaków:

• Dodatnia * Dodatnia = Dodatnia (np. 2 * 3 = 6)
• Ujemna * Ujemna = Dodatnia (np. -2 * -3 = 6)
• Dodatnia * Ujemna = Ujemna (np. 2 * -3 = -6)
• Ujemna * Dodatnia = Ujemna (np. -2 * 3 = -6)

Widzimy zatem, że jeżeli mnożymy dwie liczby o tym samym znaku (obie dodatnie lub obie ujemne), wynik jest zawsze dodatni. Jeżeli natomiast mnożymy dwie liczby o różnych znakach (jedna dodatnia, druga ujemna), wynik jest zawsze ujemny.

Przykłady:

• 5 * 7 = 35
• (-4) * (-6) = 24
• 8 * (-2) = -16
• (-9) * 3 = -27

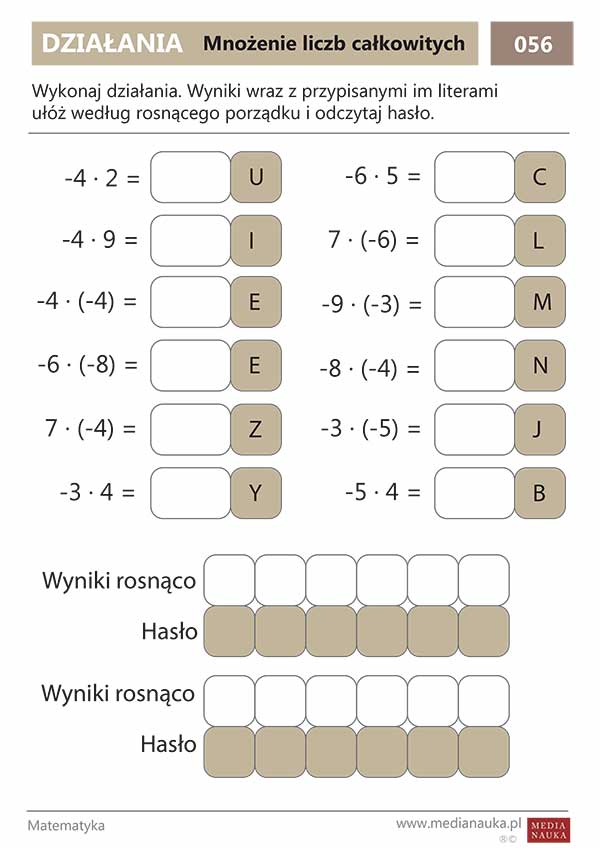
Ćwiczenia:

Oblicz:

a) 6 * 9 = ? b) (-7) * (-5) = ? c) 10 * (-3) = ? d) (-12) * 4 = ?

Rozwiązania:

a) 54 b) 35 c) -30 d) -48

Ważne jest, by dobrze opanować te zasady, ponieważ będą one obowiązywały również w bardziej skomplikowanych obliczeniach.

Dzielenie liczb całkowitych

Dzielenie, podobnie jak mnożenie, ma swoje zasady dotyczące znaków. Dzielenie to operacja odwrotna do mnożenia. Na przykład, 12 / 3 = 4, ponieważ 4 * 3 = 12. Podobnie jak w przypadku mnożenia, znaki odgrywają kluczową rolę:

• Dodatnia / Dodatnia = Dodatnia (np. 6 / 2 = 3)
• Ujemna / Ujemna = Dodatnia (np. -6 / -2 = 3)
• Dodatnia / Ujemna = Ujemna (np. 6 / -2 = -3)
• Ujemna / Dodatnia = Ujemna (np. -6 / 2 = -3)

Zasady są identyczne jak w mnożeniu. Jeżeli dzielimy dwie liczby o tym samym znaku, wynik jest dodatni. Jeżeli dzielimy dwie liczby o różnych znakach, wynik jest ujemny.

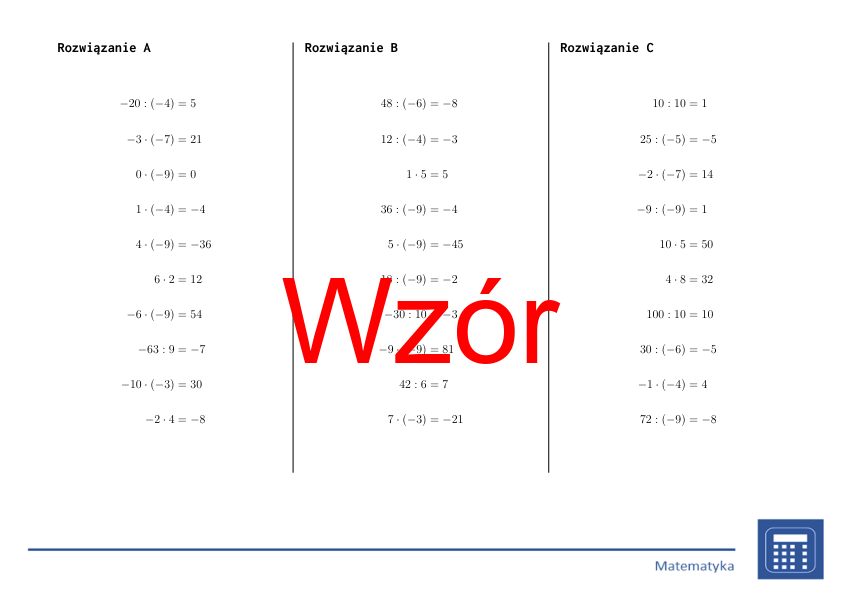
Przykłady:

• 15 / 3 = 5
• (-20) / (-4) = 5
• 25 / (-5) = -5
• (-36) / 9 = -4

Ćwiczenia:

Oblicz:

a) 24 / 6 = ? b) (-35) / (-7) = ? c) 40 / (-8) = ? d) (-48) / 12 = ?

Rozwiązania:

a) 4 b) 5 c) -5 d) -4

Należy pamiętać, że dzielenie przez zero jest niedozwolone! Nie możemy podzielić żadnej liczby przez zero. Jest to operacja nieokreślona.

Mnożenie i dzielenie z większą liczbą czynników

Co się stanie, gdy mamy do pomnożenia lub podzielenia więcej niż dwie liczby? W takim przypadku, obliczenia wykonujemy po kolei, zgodnie z kolejnością działań (od lewej do prawej). Ważne jest, aby pamiętać o zasadach znaków na każdym etapie.

Przykład mnożenia:

(-2) * 3 * (-4) = (-6) * (-4) = 24

Najpierw pomnożyliśmy -2 przez 3, co dało -6. Następnie pomnożyliśmy -6 przez -4, co dało 24.

Przykład dzielenia:

36 / (-2) / (-3) = (-18) / (-3) = 6

Najpierw podzieliliśmy 36 przez -2, co dało -18. Następnie podzieliliśmy -18 przez -3, co dało 6.

Jeżeli mamy do czynienia z kombinacją mnożenia i dzielenia, również wykonujemy działania po kolei, od lewej do prawej.

Przykład:

(-12) / 2 * (-5) = (-6) * (-5) = 30

Najpierw podzieliliśmy -12 przez 2, co dało -6. Następnie pomnożyliśmy -6 przez -5, co dało 30.

Kolejność Działań

Pamiętajmy o kolejności działań! Jeśli w wyrażeniu występują nawiasy, najpierw wykonujemy działania w nawiasach. Potem wykonujemy mnożenie i dzielenie (od lewej do prawej), a na końcu dodawanie i odejmowanie (również od lewej do prawej). To bardzo ważny aspekt, który często bywa przyczyną błędów.

Przykład:

2 * (3 + (-5)) = 2 * (-2) = -4

Najpierw obliczyliśmy wynik w nawiasie: 3 + (-5) = -2. Następnie pomnożyliśmy 2 przez -2, co dało -4.

Inny przykład:

10 – 2 * (-3) = 10 – (-6) = 10 + 6 = 16

Najpierw wykonaliśmy mnożenie: 2 * (-3) = -6. Następnie odjęliśmy -6 od 10. Pamiętamy, że odjęcie liczby ujemnej jest równoznaczne z dodaniem liczby dodatniej.

Mnożenie i dzielenie liczb całkowitych to umiejętność, którą warto ćwiczyć. Im więcej rozwiązujemy zadań, tym lepiej rozumiemy zasady i unikamy błędów. Zwracajmy uwagę na znaki i kolejność działań, a sukces jest gwarantowany! Poświęćmy czas na rozwiązywanie różnorodnych zadań, aby utrwalić zdobytą wiedzę. Nie bójmy się pytać nauczyciela lub szukać pomocy online, jeśli napotkamy trudności. Pamiętajmy, że każdy krok w matematyce prowadzi nas dalej i otwiera nowe możliwości.

Powodzenia w dalszej nauce matematyki! Pamiętaj, że regularna praktyka i systematyczność to klucz do sukcesu. Im więcej czasu poświęcisz na rozwiązywanie zadań, tym lepiej zrozumiesz zasady mnożenia i dzielenia liczb całkowitych i tym pewniej będziesz się czuć podczas rozwiązywania trudniejszych problemów.