Matematyka Klasa 5 Pola Figur

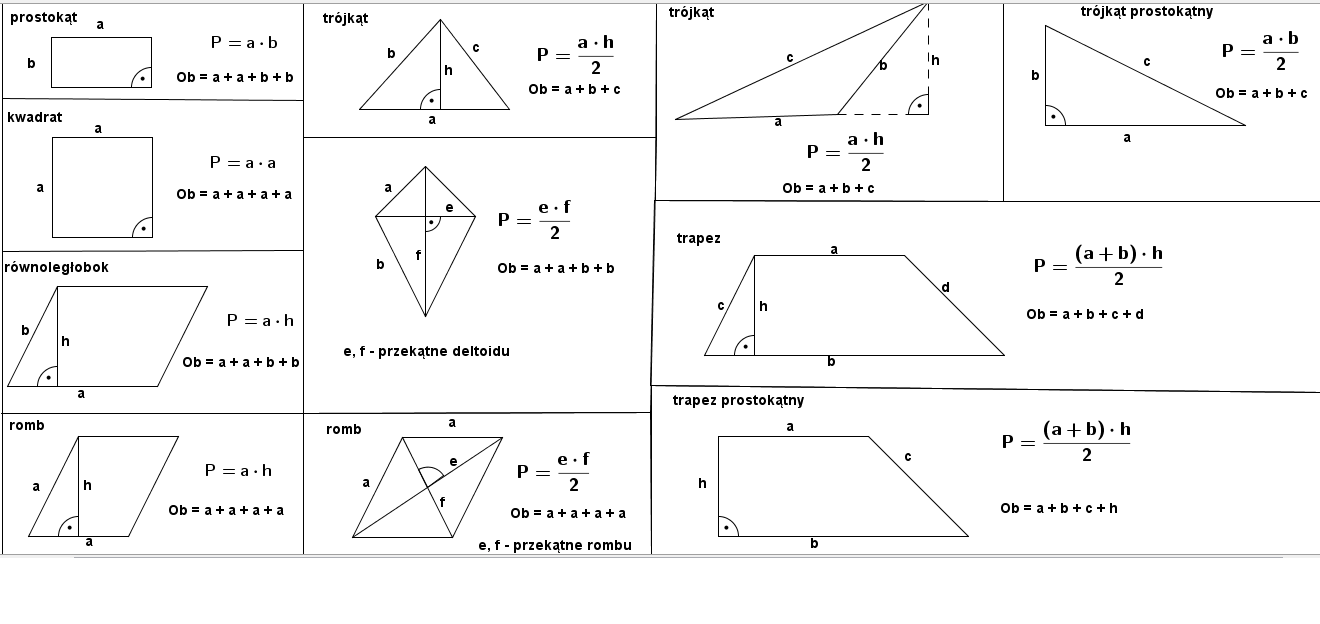
Hej, uczniowie klasy 5! Przygotujcie się na matematyczną przygodę! Ten artykuł jest stworzony specjalnie dla Was, aby pomóc Wam zrozumieć i polubić obliczanie pól figur geometrycznych. Z nami stanie się to proste i przyjemne!

Dlaczego Pola Figur Są Takie Ważne?

Pomyślcie o tym – pola figur otaczają nas wszędzie! Pola podłogi w Waszym pokoju, powierzchnia trawnika w ogródku, wielkość ekranu telewizora – wszystko to można opisać za pomocą pola. Zrozumienie, jak obliczać pola figur, pozwoli Wam mierzyć, porównywać i planować różne rzeczy w życiu codziennym. Wyobraźcie sobie, że musicie pomóc rodzicom w obliczeniu ile farby potrzebujecie do pomalowania ściany w pokoju – znajomość obliczania pola prostokąta będzie niezastąpiona! Bez obaw, to nie jest trudne!

W tym artykule skupimy się na:

Pojęciu pola figury.
Obliczaniu pola prostokąta i kwadratu.
Obliczaniu pola równoległoboku i rombu.
Obliczaniu pola trójkąta.
Rozwiązywaniu zadań tekstowych związanych z polami figur.

Co to Właściwie Jest Pole Figury?

Pole figury to miara powierzchni, jaką ta figura zajmuje. Wyobraźcie sobie, że macie kartkę papieru i rysujecie na niej prostokąt. Pole tego prostokąta to ilość miejsca, które on zajmuje na tej kartce. Pola mierzymy w jednostkach kwadratowych, takich jak centymetry kwadratowe (cm²), metry kwadratowe (m²), kilometry kwadratowe (km²) i tak dalej. Centymetr kwadratowy (cm²) to pole kwadratu o boku długości 1 cm.

Jednostki Pola:

Centymetr kwadratowy (cm²): Mały kwadrat – idealny do mierzenia powierzchni w zeszycie.
Metr kwadratowy (m²): Większy kwadrat – dobry do mierzenia powierzchni pokoju.
Kilometr kwadratowy (km²): Ogromny kwadrat – odpowiedni do mierzenia powierzchni miast lub jezior.

Prostokąt i Kwadrat – Podstawowe Figury

Prostokąt to czworokąt, który ma cztery kąty proste. Ma dwa boki o różnej długości – nazywamy je długością (a) i szerokością (b).

Kwadrat to szczególny rodzaj prostokąta, w którym wszystkie boki są równe. Długość boku kwadratu oznaczamy zwykle jako a.

Jak Obliczyć Pole Prostokąta?

Pole prostokąta obliczamy, mnożąc jego długość przez szerokość:

P = a * b

Przykład: Prostokąt ma długość 5 cm i szerokość 3 cm. Jego pole wynosi:

P = 5 cm * 3 cm = 15 cm²

Jak Obliczyć Pole Kwadratu?

Ponieważ kwadrat ma wszystkie boki równe, jego pole obliczamy, mnożąc długość boku przez samą siebie (czyli podnosząc długość boku do kwadratu):

P = a * a = a²

Przykład: Kwadrat ma bok długości 4 cm. Jego pole wynosi:

P = 4 cm * 4 cm = 16 cm²

Równoległobok i Romb – Figury z Przesunięciem

Równoległobok to czworokąt, który ma dwie pary boków równoległych. Podobnie jak prostokąt, ma dwa boki o różnej długości. Do obliczenia pola równoległoboku potrzebna jest nam wysokość (h), czyli odległość między dwoma równoległymi bokami. Ważne! Wysokość musi być prostopadła do boku.

Romb to równoległobok, który ma wszystkie boki równe. Można go wyobrazić sobie jako "ściśnięty" kwadrat. Podobnie jak równoległobok, do obliczenia jego pola potrzebna jest wysokość (h).

Jak Obliczyć Pole Równoległoboku?

Pole równoległoboku obliczamy, mnożąc długość podstawy (a) przez wysokość (h) opuszczoną na tę podstawę:

P = a * h

Przykład: Równoległobok ma podstawę długości 6 cm i wysokość opuszczoną na tę podstawę równą 4 cm. Jego pole wynosi:

P = 6 cm * 4 cm = 24 cm²

Jak Obliczyć Pole Rombu?

Pole rombu możemy obliczyć na dwa sposoby:

Tak samo jak pole równoległoboku: P = a * h (gdzie a to długość boku, a h to wysokość).
Mnożąc długości jego przekątnych (e i f) i dzieląc wynik przez 2: P = (e * f) / 2

Przykład 1 (używając podstawy i wysokości): Romb ma bok długości 5 cm i wysokość równą 3 cm. Jego pole wynosi:

P = 5 cm * 3 cm = 15 cm²

Przykład 2 (używając przekątnych): Romb ma przekątne długości 8 cm i 6 cm. Jego pole wynosi:

P = (8 cm * 6 cm) / 2 = 48 cm² / 2 = 24 cm²

Trójkąt – Połowa Równoległoboku

Trójkąt to figura, która ma trzy boki i trzy kąty. Podobnie jak w przypadku równoległoboku, do obliczenia pola trójkąta potrzebujemy podstawy (a) i wysokości (h) opuszczonej na tę podstawę. Wysokość trójkąta to odcinek poprowadzony z wierzchołka trójkąta prostopadle do przeciwległego boku (lub jego przedłużenia).

Jak Obliczyć Pole Trójkąta?

Pole trójkąta obliczamy, mnożąc długość podstawy (a) przez wysokość (h) opuszczoną na tę podstawę i dzieląc wynik przez 2:

P = (a * h) / 2

Dlaczego dzielimy przez 2? Wyobraźcie sobie, że rysujecie drugi, identyczny trójkąt i doklejacie go do pierwszego tak, aby powstał równoległobok. Pole tego równoległoboku to a * h, a pole każdego trójkąta to połowa pola równoległoboku.

Przykład: Trójkąt ma podstawę długości 7 cm i wysokość opuszczoną na tę podstawę równą 4 cm. Jego pole wynosi:

P = (7 cm * 4 cm) / 2 = 28 cm² / 2 = 14 cm²

Zadania Tekstowe – Pola w Praktyce

Teraz czas na praktykę! Rozwiążemy kilka zadań tekstowych, żeby zobaczyć, jak możemy wykorzystać naszą wiedzę o polach figur w prawdziwych sytuacjach.

Zadanie 1: Pokój ma kształt prostokąta o wymiarach 4 m x 3 m. Ile metrów kwadratowych parkietu potrzeba do wyłożenia podłogi?

Rozwiązanie:

P = a * b = 4 m * 3 m = 12 m²

Odpowiedź: Potrzeba 12 metrów kwadratowych parkietu.

Zadanie 2: Trawnik ma kształt rombu, którego przekątne mają długość 10 m i 8 m. Ile metrów kwadratowych trawy rośnie na tym trawniku?

Rozwiązanie:

P = (e * f) / 2 = (10 m * 8 m) / 2 = 80 m² / 2 = 40 m²

Odpowiedź: Na trawniku rośnie 40 metrów kwadratowych trawy.

Zadanie 3: Żagiel w łódce ma kształt trójkąta o podstawie długości 3 m i wysokości 2 m. Jakie jest pole powierzchni żagla?

Rozwiązanie:

P = (a * h) / 2 = (3 m * 2 m) / 2 = 6 m² / 2 = 3 m²

Odpowiedź: Pole powierzchni żagla wynosi 3 metry kwadratowe.

Kilka Dodatkowych Wskazówek:

Zawsze zwracaj uwagę na jednostki! Upewnij się, że wszystkie wymiary są podane w tej samej jednostce (np. cm, m).
Rysuj! Narysuj sobie figurę geometryczną, o której mowa w zadaniu. To pomoże Ci zrozumieć, o co pytają.
Sprawdzaj! Po obliczeniu pola, zastanów się, czy wynik ma sens. Czy pole Twojego pokoju może wynosić 1000 m²? Raczej nie!

Pamiętajcie, że ćwiczenie czyni mistrza! Rozwiązujcie dużo zadań, a obliczanie pól figur stanie się dla Was bułką z masłem. Nie bójcie się pytać nauczyciela o pomoc, jeśli czegoś nie rozumiecie. Jesteście wspaniali i na pewno dacie radę! Powodzenia!

Mam nadzieję, że ten artykuł pomógł Wam lepiej zrozumieć pola figur geometrycznych. Pamiętajcie, że matematyka może być fascynująca i przydatna w życiu codziennym. Teraz idźcie i zmierzcie świat!