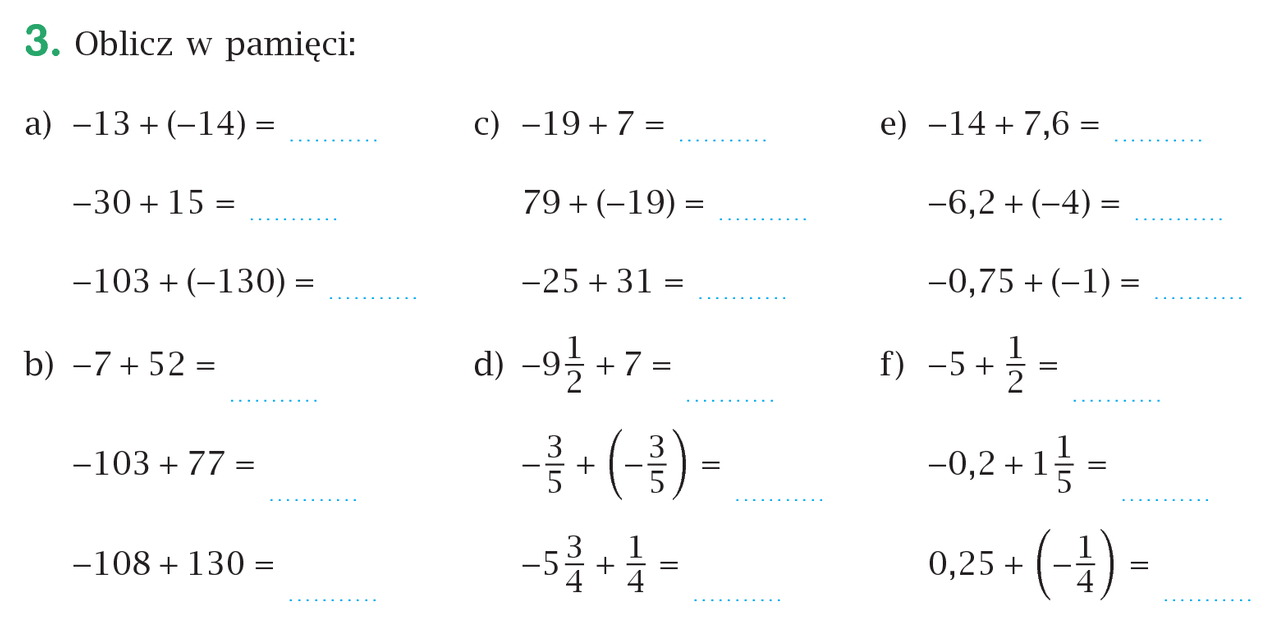Matematyka Klasa 5 Liczby Całkowite

Witaj w fascynującym świecie liczb całkowitych! W klasie 5 rozpoczynamy przygodę z liczbami, które są większe niż tylko te, które znamy z liczenia. Liczby całkowite otwierają przed nami nowe możliwości w rozwiązywaniu problemów i zrozumieniu otaczającego nas świata. Przygotuj się na ekscytującą podróż!

Czym są Liczby Całkowite?

Liczby całkowite to zbiór liczb składający się z liczb naturalnych (1, 2, 3, ...), zera (0) oraz liczb przeciwnych do liczb naturalnych (-1, -2, -3, ...). Inaczej mówiąc, są to wszystkie liczby bez ułamków i części dziesiętnych, zarówno dodatnie, jak i ujemne, oraz zero. Zbiór liczb całkowitych oznaczamy literą Z.

Liczby naturalne, które już znamy, to liczby służące do liczenia przedmiotów: 1, 2, 3, 4, 5... Zero (0) reprezentuje brak czegoś. Natomiast liczby ujemne (np. -1, -2, -3) reprezentują wartości mniejsze od zera.

Oś Liczbowa

Najlepszym sposobem na wizualizację liczb całkowitych jest oś liczbowa. Wyobraź sobie prostą linię. W jej środku znajduje się zero (0). Na prawo od zera, w równych odstępach, znajdują się liczby dodatnie: 1, 2, 3, 4 i tak dalej. Na lewo od zera, również w równych odstępach, znajdują się liczby ujemne: -1, -2, -3, -4 i tak dalej. Im dalej na prawo od zera, tym liczba jest większa. Im dalej na lewo od zera, tym liczba jest mniejsza.

Pamiętaj: -5 jest mniejsze niż -2, ponieważ -5 leży bardziej na lewo na osi liczbowej.

Porównywanie Liczb Całkowitych

Kiedy mówimy o porównywaniu liczb całkowitych, chcemy ustalić, która liczba jest większa, mniejsza, lub czy są one równe. Używamy do tego symboli:

> (większy niż)
< (mniejszy niż)
= (równy)

Zasady porównywania liczb całkowitych:

Każda liczba dodatnia jest większa od zera.
Zero jest większe od każdej liczby ujemnej.
Każda liczba dodatnia jest większa od każdej liczby ujemnej.
Spośród dwóch liczb dodatnich, większa jest ta, która jest dalej od zera na osi liczbowej.
Spośród dwóch liczb ujemnych, większa jest ta, która jest bliżej zera na osi liczbowej (np. -1 jest większe niż -5).

Przykłady:

5 > 2 (5 jest większe niż 2)
-3 < 1 ( -3 jest mniejsze niż 1)
0 > -4 (0 jest większe niż -4)
-1 > -6 (-1 jest większe niż -6)

Działania na Liczbach Całkowitych

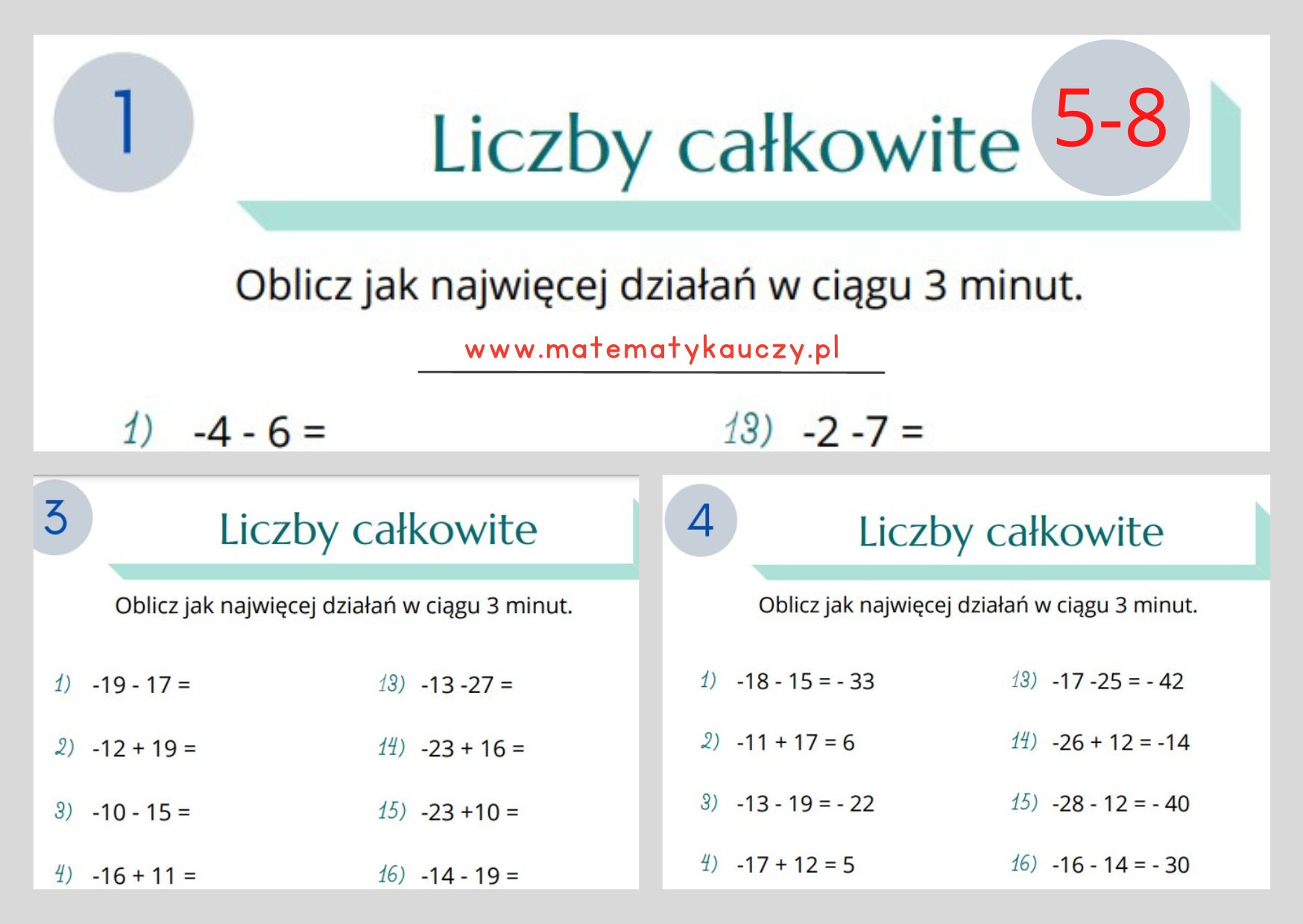
Liczby całkowite, tak jak liczby naturalne, możemy dodawać, odejmować, mnożyć i dzielić. Należy jednak pamiętać o znakach liczb.

Dodawanie Liczb Całkowitych

Dodawanie liczb o tych samych znakach jest proste. Dodajemy ich wartości bezwzględne, a wynik ma ten sam znak, co dodawane liczby.

Przykłady:

3 + 5 = 8 (Dodawanie dwóch liczb dodatnich)
-2 + (-4) = -6 (Dodawanie dwóch liczb ujemnych)

Dodawanie liczb o różnych znakach wymaga trochę więcej uwagi. Odejmujemy od większej wartości bezwzględnej mniejszą wartość bezwzględną, a wynik ma znak liczby o większej wartości bezwzględnej.

Przykłady:

-7 + 4 = -3 (Wartość bezwzględna -7 to 7, a 4 to 4. 7 - 4 = 3. Wynik ma znak minus, bo -7 ma większą wartość bezwzględną niż 4.)
5 + (-2) = 3 (Wartość bezwzględna 5 to 5, a -2 to 2. 5 - 2 = 3. Wynik ma znak plus, bo 5 ma większą wartość bezwzględną niż -2.)

Odejmowanie Liczb Całkowitych

Odejmowanie liczb całkowitych można zamienić na dodawanie, dodając liczbę przeciwną do liczby odejmowanej.

Przykłady:

5 - 3 = 5 + (-3) = 2
2 - (-4) = 2 + 4 = 6
-1 - 2 = -1 + (-2) = -3
-3 - (-5) = -3 + 5 = 2

Mnożenie i Dzielenie Liczb Całkowitych

Mnożenie i dzielenie liczb całkowitych rządzi się prostymi zasadami znaków:

Dodatnia * Dodatnia = Dodatnia
Ujemna * Ujemna = Dodatnia
Dodatnia * Ujemna = Ujemna
Ujemna * Dodatnia = Ujemna

Te same zasady dotyczą dzielenia.

Przykłady:

3 * 4 = 12
-2 * (-5) = 10
-3 * 2 = -6
10 / 2 = 5
-12 / (-3) = 4
-8 / 2 = -4

Praktyczne Zastosowanie Liczb Całkowitych

Liczby całkowite są obecne w wielu aspektach naszego życia. Oto kilka przykładów:

Temperatura: Temperatura może być wyrażona za pomocą liczb ujemnych (np. -5 stopni Celsjusza) i dodatnich (np. 25 stopni Celsjusza).
Długi i zyski: Możemy reprezentować długi za pomocą liczb ujemnych (np. -100 zł długu), a zyski za pomocą liczb dodatnich (np. 200 zł zysku).
Położenie: Wysokość nad poziomem morza może być wyrażona jako liczba dodatnia, a głębokość poniżej poziomu morza jako liczba ujemna. Na przykład, Rysy mają wysokość 2499 m n.p.m., a najgłębszy punkt Rowu Mariańskiego znajduje się na głębokości około -11000 m.
Historia: Lata przed naszą erą często oznaczane są liczbami ujemnymi, np. rok -50 p.n.e.
Gry: W wielu grach punktacja może być ujemna, jeśli gracz popełnia błędy lub traci punkty.

Przykład 1: Wyobraź sobie, że masz na koncie 50 zł. Potem wypłacasz 80 zł. Ile masz teraz na koncie? Możemy to zapisać jako 50 - 80 = -30. Masz -30 zł, czyli jesteś na minusie.

Przykład 2: Dziś temperatura wynosi 2 stopnie Celsjusza. W nocy temperatura spadnie o 5 stopni. Jaka będzie temperatura w nocy? Możemy to zapisać jako 2 - 5 = -3. Temperatura w nocy wyniesie -3 stopnie Celsjusza.

"Zrozumienie liczb całkowitych jest kluczowe dla dalszej nauki matematyki i dla rozwiązywania wielu problemów w życiu codziennym."

Podsumowanie i Ćwiczenia

Gratulacje! Dotarliśmy do końca naszej podróży po świecie liczb całkowitych. Pamiętaj, że liczby całkowite to liczby naturalne, zero i liczby ujemne. Nauczyliśmy się je porównywać i wykonywać na nich działania.

Aby utrwalić zdobytą wiedzę, spróbuj rozwiązać kilka zadań:

Porównaj liczby: -7 i -3, 4 i -1, 0 i -5.
Oblicz: -5 + 2, 3 - 7, -2 * 4, -10 / (-2).
Jaka będzie temperatura, jeśli teraz jest -2 stopnie, a temperatura wzrośnie o 6 stopni?
Masz dług w wysokości 20 zł. Zarobiłeś 50 zł. Ile masz teraz pieniędzy?

Pamiętaj, praktyka czyni mistrza! Im więcej ćwiczysz, tym lepiej zrozumiesz liczby całkowite. Powodzenia!

Jeśli masz jakieś pytania, śmiało zapytaj nauczyciela lub poszukaj odpowiedzi w podręczniku. Nie bój się wyzwań! Matematyka może być fascynującą przygodą.