Magiczne Kwadraty Klasa 3 Zadania

Magiczne kwadraty to fascynujące zagadnienie matematyczne, które doskonale nadaje się do rozwijania umiejętności logicznego myślenia i kreatywności u dzieci, zwłaszcza w klasie 3. W tym artykule przyjrzymy się bliżej magicznym kwadratom, skupiając się na zadaniach odpowiednich dla uczniów tej grupy wiekowej. Zrozumiemy, czym są, jak je rozwiązywać, i dlaczego są tak wartościowe w edukacji matematycznej.

Czym są Magiczne Kwadraty?

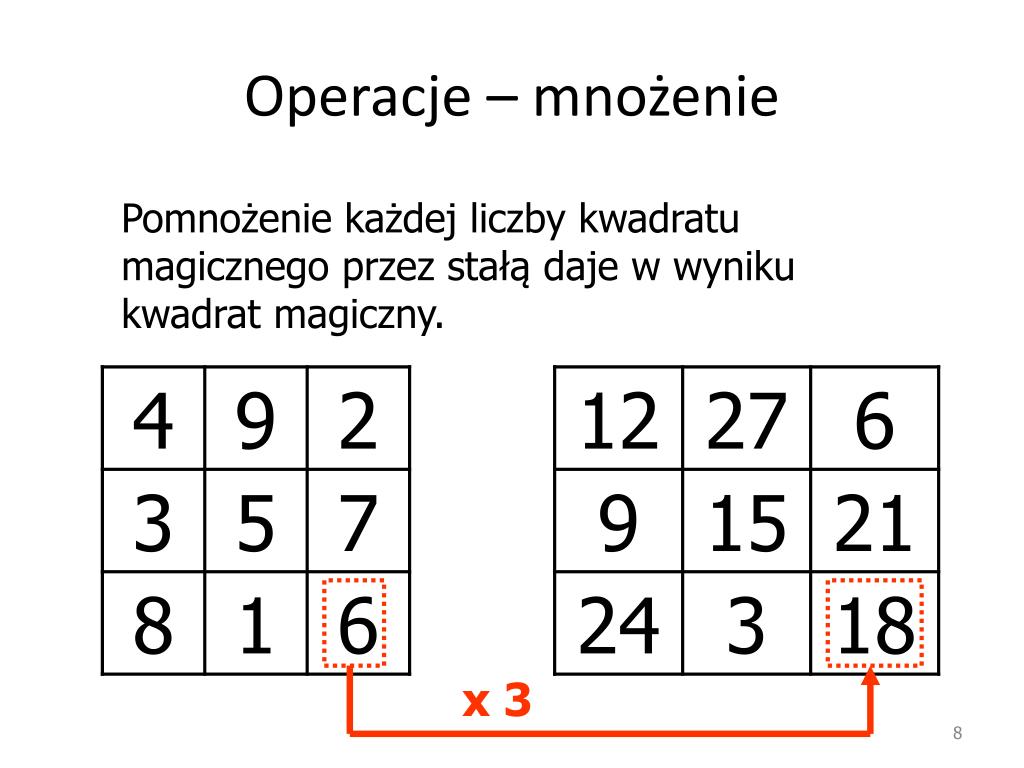
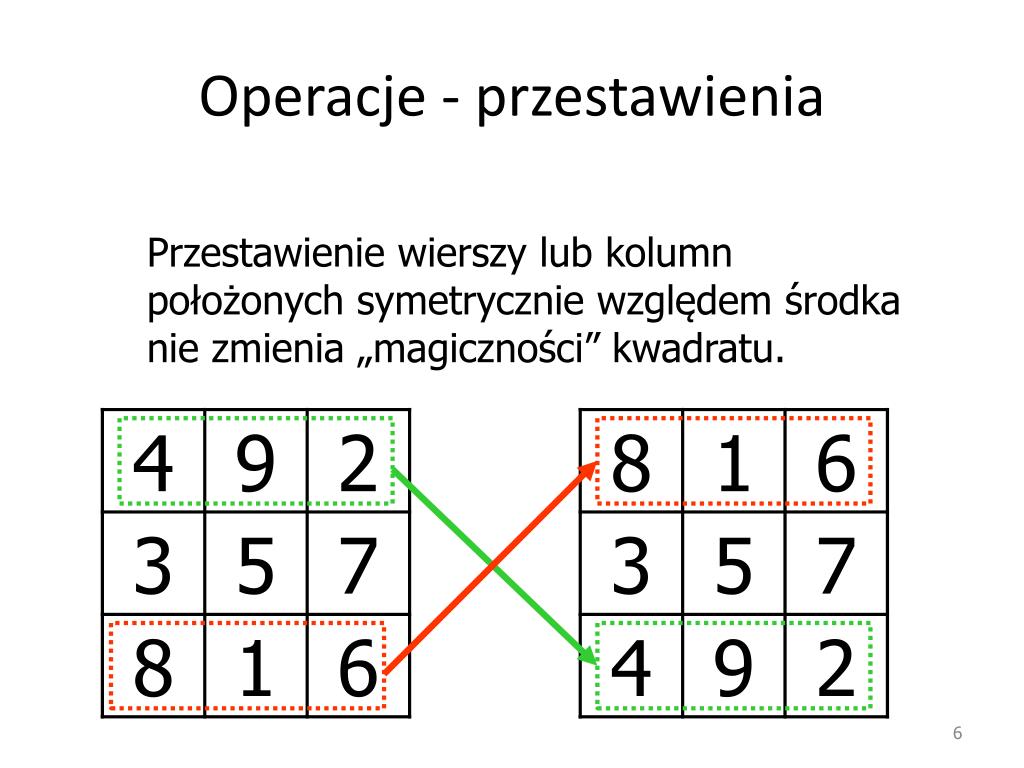
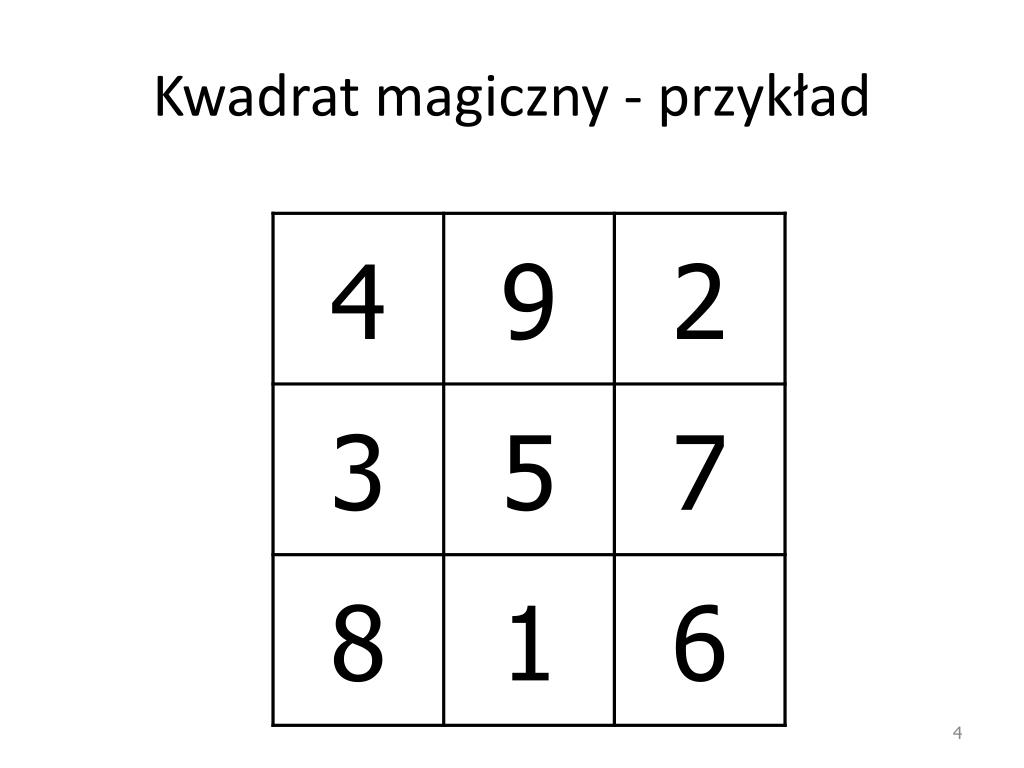
Magiczny kwadrat to kwadratowa siatka wypełniona różnymi liczbami, zazwyczaj kolejnymi liczbami naturalnymi, w taki sposób, że suma liczb w każdym wierszu, każdej kolumnie i każdej przekątnej jest taka sama. Ta stała suma nazywana jest magiczną stałą lub liczbą magiczną kwadratu.

Dla przykładu, w magicznym kwadracie 3x3 używającym liczb od 1 do 9, magiczna stała wynosi 15. Oznacza to, że suma liczb w każdym wierszu, każdej kolumnie i każdej przekątnej musi być równa 15.

Dlaczego Magiczne Kwadraty są Dobre dla Dzieci?

Praca z magicznymi kwadratami przynosi dzieciom wiele korzyści:

Rozwija umiejętność logicznego myślenia: Dzieci muszą analizować zależności między liczbami i szukać wzorców, aby poprawnie wypełnić kwadrat.
Wspomaga zdolności matematyczne: Ćwiczą dodawanie, odejmowanie i szacowanie, a także rozumienie zależności liczbowych.
Uczy cierpliwości i wytrwałości: Rozwiązywanie magicznych kwadratów wymaga skupienia i często metod prób i błędów.
Pobudza kreatywność: Chociaż istnieje logiczne rozwiązanie, dzieci mogą eksperymentować z różnymi kombinacjami liczb, aby znaleźć rozwiązanie.
Wzmacnia poczucie sukcesu: Ukończenie magicznego kwadratu daje dziecku satysfakcję i poczucie sprawstwa.

Zadania z Magicznymi Kwadratami dla Klasy 3

Dla dzieci w klasie 3, zadania z magicznymi kwadratami powinny być odpowiednio dostosowane do ich poziomu umiejętności. Najczęściej spotykane są kwadraty 3x3, gdzie niektóre pola są już wypełnione, a zadaniem dziecka jest uzupełnienie pozostałych.

Przykładowe Zadanie 1:

Wypełnij poniższy magiczny kwadrat 3x3, używając liczb od 1 do 9. Pamiętaj, że suma liczb w każdym wierszu, każdej kolumnie i każdej przekątnej musi być równa 15.

 +---+---+---+
 | 8 |   |   |
 +---+---+---+
 |   | 5 |   |
 +---+---+---+
 |   |   | 2 |
 +---+---+---+

Rozwiązanie:

 +---+---+---+
 | 8 | 1 | 6 |
 +---+---+---+
 | 3 | 5 | 7 |
 +---+---+---+
 | 4 | 9 | 2 |
 +---+---+---+

Przykładowe Zadanie 2:

Uzupełnij magiczny kwadrat 3x3, wiedząc, że magiczna stała wynosi 12 i używasz liczb od 2 do 10 (nie wszystkie liczby muszą być użyte!).

 +---+---+---+
 |   | 7 |   |
 +---+---+---+
 |   | 4 |   |
 +---+---+---+
 |   |   |   |
 +---+---+---+

Rozwiązanie: (Przykładowe, istnieje więcej rozwiązań)

 +---+---+---+
 | 3 | 7 | 2 |
 +---+---+---+
 | 5 | 4 | 3 |
 +---+---+---+
 | 4 | 1 | 7 |
 +---+---+---+

Przykładowe Zadanie 3:

Która liczba powinna znaleźć się w miejscu znaku zapytania, aby poniższy kwadrat był magiczny? Używasz liczb od 1 do 9, a magiczna suma wynosi 15.

 +---+---+---+
 | 6 | 1 | 8 |
 +---+---+---+
 | 7 | 5 | 3 |
 +---+---+---+
 | 2 | ? | 4 |
 +---+---+---+

Rozwiązanie:

Szukana liczba to 9.

Strategie Rozwiązywania Magiczych Kwadratów

Istnieją różne strategie, które dzieci mogą wykorzystać do rozwiązywania magicznych kwadratów. Oto kilka z nich:

Obliczanie magicznej stałej: Jeśli znamy wszystkie liczby, które mają być użyte, możemy obliczyć magiczną stałą, sumując wszystkie liczby i dzieląc wynik przez liczbę wierszy (lub kolumn). Na przykład, dla liczb od 1 do 9, suma wynosi 45, a 45 / 3 = 15.
Szukanie brakujących liczb w wierszach, kolumnach i przekątnych: Jeśli znamy dwie liczby w wierszu, kolumnie lub przekątnej, możemy obliczyć brakującą liczbę, odejmując sumę znanych liczb od magicznej stałej.
Stosowanie metody prób i błędów: Dzieci mogą eksperymentować z różnymi kombinacjami liczb, sprawdzając, czy suma w wierszach, kolumnach i przekątnych jest równa magicznej stałej. Ważne jest, aby zachęcać je do systematycznego sprawdzania i notowania swoich prób.
Szukanie wzorców: W niektórych magicznych kwadratach można zauważyć pewne wzorce, które ułatwiają rozwiązanie. Na przykład, w standardowym magicznym kwadracie 3x3 liczba 5 zawsze znajduje się w środku.

Magiczne Kwadraty w Realnym Świecie

Chociaż magiczne kwadraty mogą wydawać się abstrakcyjnym zagadnieniem matematycznym, mają swoje korzenie w historii i można je znaleźć w różnych kulturach. Uważano je za symbole magiczne i religijne. Współcześnie, magiczne kwadraty są nadal wykorzystywane w rekreacji, edukacji i nawet w pewnych algorytmach komputerowych.

Co więcej, zasady rządzące magicznymi kwadratami znajdują zastosowanie w bardziej zaawansowanych dziedzinach matematyki, takich jak teoria liczb i kombinatoryka. Dzieci, które w młodym wieku zapoznają się z magicznymi kwadratami, mogą w przyszłości łatwiej zrozumieć te bardziej złożone koncepcje.

Dostępne Materiały i Zasoby

W internecie i w księgarniach można znaleźć wiele materiałów i zasobów poświęconych magicznym kwadratom. Warto poszukać:

Książek z zadaniami: Istnieją książki specjalnie dedykowane magicznym kwadratom, zawierające zadania o różnym stopniu trudności.
Stron internetowych i aplikacji: Wiele stron internetowych i aplikacji oferuje interaktywne magiczne kwadraty, które można rozwiązywać online.
Generatorów magicznych kwadratów: Można znaleźć generatory, które automatycznie tworzą magiczne kwadraty, pozwalając na tworzenie własnych zadań.
Darmowych kart pracy: Wiele stron edukacyjnych oferuje darmowe karty pracy z magicznymi kwadratami do wydrukowania.

Podsumowanie i Zachęta do Działania

Magiczne kwadraty to świetny sposób na rozwijanie umiejętności matematycznych i logicznego myślenia u dzieci w klasie 3. Są zabawne, angażujące i oferują poczucie sukcesu. Zachęcam rodziców i nauczycieli do włączenia magicznych kwadratów do edukacji matematycznej. Rozpocznijcie od prostych zadań i stopniowo zwiększajcie poziom trudności. Obserwujcie, jak dzieci zyskują pewność siebie i radość z rozwiązywania problemów!

Spróbujcie rozwiązać magiczny kwadrat 3x3 z użyciem liczb od 4 do 12 (suma magiczna wynosi 24). To świetny sposób na utrwalenie wiedzy i sprawdzenie swoich umiejętności.

Pamiętaj, że kluczem do sukcesu jest cierpliwość i pozytywne nastawienie. Powodzenia!