Liczby Wymierne Test 1 Gimnazjum

Zastanawiasz się, jak najlepiej przygotować się do sprawdzianu z liczb wymiernych w gimnazjum? A może chcesz po prostu przypomnieć sobie podstawowe definicje i operacje? Ten artykuł jest dla Ciebie! Stworzony z myślą o uczniach klas 7 i 8, pomoże Ci zrozumieć kluczowe zagadnienia związane z liczbami wymiernymi i skutecznie rozwiązywać zadania.

Czym są Liczby Wymierne? Definicja i Przykłady

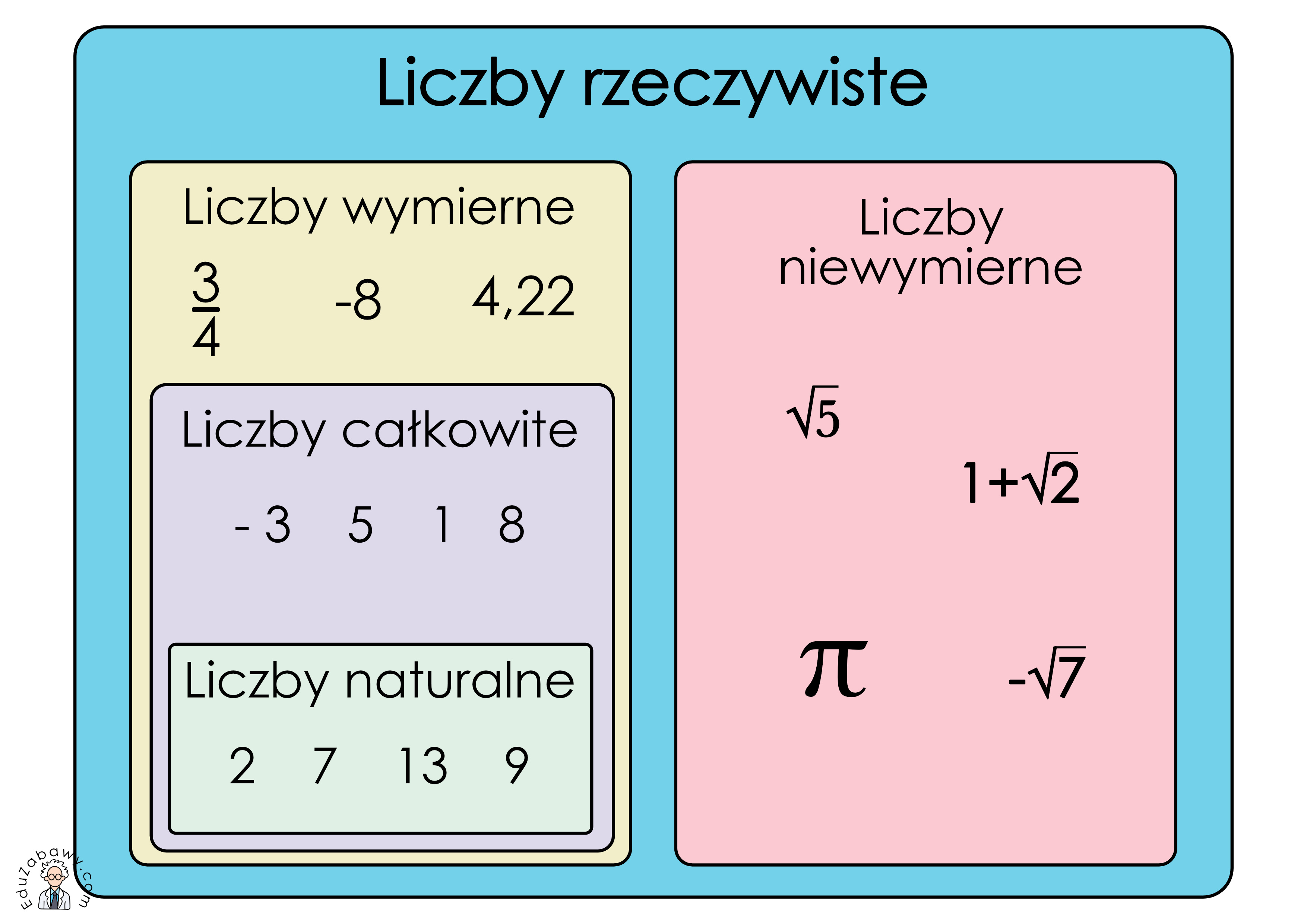
Liczby wymierne to takie liczby, które można przedstawić w postaci ułamka a/b, gdzie a jest liczbą całkowitą, a b jest liczbą całkowitą różną od zera. Inaczej mówiąc, to liczby, które możemy zapisać jako iloraz dwóch liczb całkowitych.

Przykłady Liczb Wymiernych:

Ułamki zwykłe: 1/2, 3/4, -5/7
Liczby całkowite: 5 (można zapisać jako 5/1), -3 (można zapisać jako -3/1)
Ułamki dziesiętne skończone: 0.25 (można zapisać jako 1/4), -1.5 (można zapisać jako -3/2)
Ułamki dziesiętne okresowe: 0.(3) (czyli 0.333...), 1.(6) (czyli 1.666...)

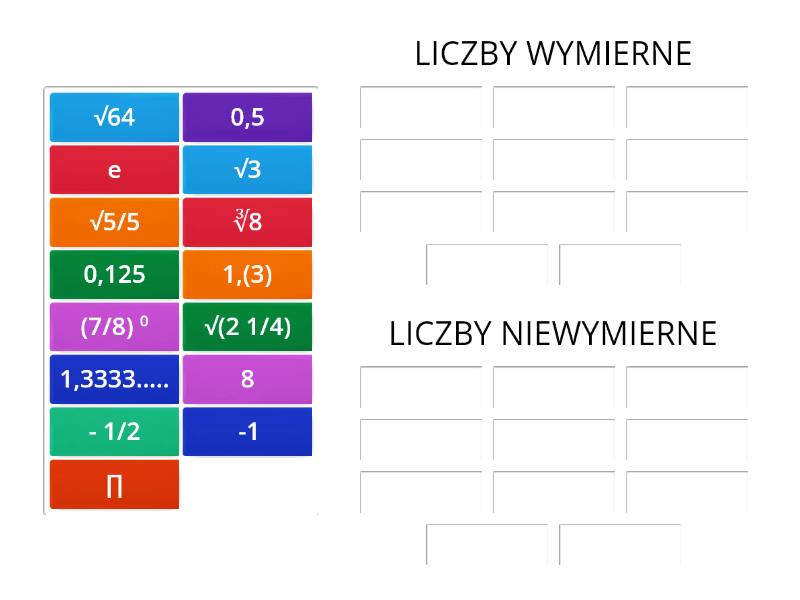
Pamiętaj, że liczby niewymierne, takie jak π (pi) czy √2 (pierwiastek kwadratowy z 2), nie są liczbami wymiernymi, ponieważ nie można ich zapisać w postaci ułamka a/b.

Działania na Liczbach Wymiernych

Sprawne wykonywanie działań na liczbach wymiernych to podstawa sukcesu na sprawdzianie. Przyjrzyjmy się najważniejszym operacjom:

Dodawanie i Odejmowanie Ułamków

Aby dodać lub odjąć ułamki, musimy sprowadzić je do wspólnego mianownika. Wspólny mianownik to najmniejsza wspólna wielokrotność mianowników ułamków, które chcemy dodać lub odjąć.

Przykład:

Oblicz: 1/3 + 1/4

Znajdujemy wspólny mianownik: NWW(3, 4) = 12
Sprowadzamy ułamki do wspólnego mianownika: 1/3 = 4/12, 1/4 = 3/12
Dodajemy ułamki: 4/12 + 3/12 = 7/12

Mnożenie Ułamków

Mnożenie ułamków jest proste: mnożymy licznik przez licznik, a mianownik przez mianownik.

Przykład:

Oblicz: 2/5 * 3/7

2/5 * 3/7 = (2 * 3) / (5 * 7) = 6/35

Dzielenie Ułamków

Dzielenie ułamków to tak naprawdę mnożenie przez odwrotność drugiego ułamka.

Przykład:

Oblicz: 1/2 : 3/4

1/2 : 3/4 = 1/2 * 4/3 = (1 * 4) / (2 * 3) = 4/6 = 2/3

Działania na Ułamkach Dziesiętnych

Dodawanie, odejmowanie, mnożenie i dzielenie ułamków dziesiętnych wykonujemy podobnie jak na liczbach całkowitych, pamiętając o wyrównaniu przecinków.

Przykład:

Oblicz: 2.5 + 1.75

Wyrównujemy przecinki: 2.50 + 1.75 = 4.25

Porównywanie Liczb Wymiernych

Aby porównać liczby wymierne, możemy sprowadzić je do wspólnego mianownika lub zamienić na ułamki dziesiętne. Liczba o większym liczniku (przy wspólnym mianowniku) lub większej wartości dziesiętnej jest większa.

Przykład:

Która liczba jest większa: 2/3 czy 3/5?

Sprowadzamy do wspólnego mianownika: 2/3 = 10/15, 3/5 = 9/15
Porównujemy liczniki: 10 > 9, więc 2/3 > 3/5

Zadania Typu "Sprawdzian" i Jak Je Rozwiązywać

Na sprawdzianie z liczb wymiernych możesz spodziewać się różnego rodzaju zadań. Oto kilka przykładów i wskazówki, jak je rozwiązywać:

Zadanie 1: Uprość wyrażenie.

Przykład: Uprość wyrażenie: (1/2 + 1/3) * 6 - 2/5 : 1/5

Wykonaj działania w nawiasach: 1/2 + 1/3 = 3/6 + 2/6 = 5/6
Wykonaj mnożenie: 5/6 * 6 = 5
Wykonaj dzielenie: 2/5 : 1/5 = 2/5 * 5/1 = 2
Wykonaj odejmowanie: 5 - 2 = 3

Odpowiedź: 3

Zadanie 2: Rozwiąż równanie.

Przykład: Rozwiąż równanie: 2x + 1/4 = 3/4

Przenieś 1/4 na prawą stronę równania: 2x = 3/4 - 1/4
Wykonaj odejmowanie: 2x = 2/4 = 1/2
Podziel obie strony równania przez 2: x = (1/2) / 2 = 1/4

Odpowiedź: x = 1/4

Zadanie 3: Zadanie tekstowe.

Przykład: Cena bluzki wzrosła o 1/5. Nowa cena bluzki wynosi 36 zł. Ile kosztowała bluzka przed podwyżką?

Oznaczamy cenę bluzki przed podwyżką jako x.
Zapisujemy równanie: x + (1/5)x = 36
Upraszczamy równanie: (6/5)x = 36
Mnożymy obie strony równania przez 5/6: x = 36 * (5/6) = 30

Odpowiedź: Bluzka kosztowała 30 zł przed podwyżką.

Praktyczne Wskazówki na Sprawdzian

Powtórz definicje: Upewnij się, że rozumiesz, czym są liczby wymierne i jak się je zapisuje.
Przećwicz zadania: Im więcej zadań rozwiążesz, tym lepiej zrozumiesz materiał. Skorzystaj z podręcznika, zbioru zadań lub internetu.
Zwracaj uwagę na znaki: Pamiętaj o prawidłowym używaniu znaków "+" i "-" przy dodawaniu, odejmowaniu, mnożeniu i dzieleniu.
Uprość wynik: Jeśli to możliwe, uprość wynik do najprostszej postaci.
Sprawdź odpowiedź: Po rozwiązaniu zadania sprawdź, czy Twoja odpowiedź ma sens. Czy cena bluzki mogła wzrosnąć o 1/5 i wynosić 36zł? Czy wynik działania jest liczbą wymierną, jeśli działaliśmy na liczbach wymiernych?
Zarządzaj czasem: Na sprawdzianie rozsądnie zarządzaj czasem. Nie poświęcaj zbyt dużo czasu na jedno zadanie, jeśli nie możesz go rozwiązać. Przejdź do kolejnego zadania i wróć do trudnego później.
Bądź spokojny: Stres może utrudnić rozwiązywanie zadań. Spróbuj się zrelaksować i skoncentrować na zadaniu. Pamiętaj o głębokich oddechach!

Gdzie Szukać Dodatkowej Pomocy?

Jeśli masz problemy z liczbami wymiernymi, nie wahaj się szukać dodatkowej pomocy:

Zapytaj nauczyciela: Twój nauczyciel jest najlepszym źródłem informacji i może pomóc Ci zrozumieć trudne zagadnienia.
Poproś o pomoc kolegę/koleżankę: Czasami wytłumaczenie od rówieśnika może być bardziej zrozumiałe.
Skorzystaj z internetu: W internecie znajdziesz wiele materiałów edukacyjnych, filmów i ćwiczeń z liczb wymiernych. Szukaj na platformach edukacyjnych i stronach dedykowanych matematyce szkolnej.
Znajdź korepetytora: Jeśli potrzebujesz indywidualnej pomocy, rozważ skorzystanie z korepetycji.

Pamiętaj, że systematyczna praca i ćwiczenia to klucz do sukcesu na sprawdzianie z liczb wymiernych. Nie zrażaj się trudnościami, a z pewnością osiągniesz swój cel! Powodzenia!