Liczby Wymierne Sprawdzian Klasa 7

Czy czeka Cię sprawdzian z liczb wymiernych w 7 klasie i czujesz lekkie (albo i spore) zdenerwowanie? Rozumiem. Liczby wymierne, choć fundamentalne, potrafią sprawić kłopot, szczególnie jeśli brakuje solidnych podstaw. Ale bez obaw! Ten artykuł pomoże Ci się do niego przygotować, uporządkować wiedzę i nabrać pewności siebie.

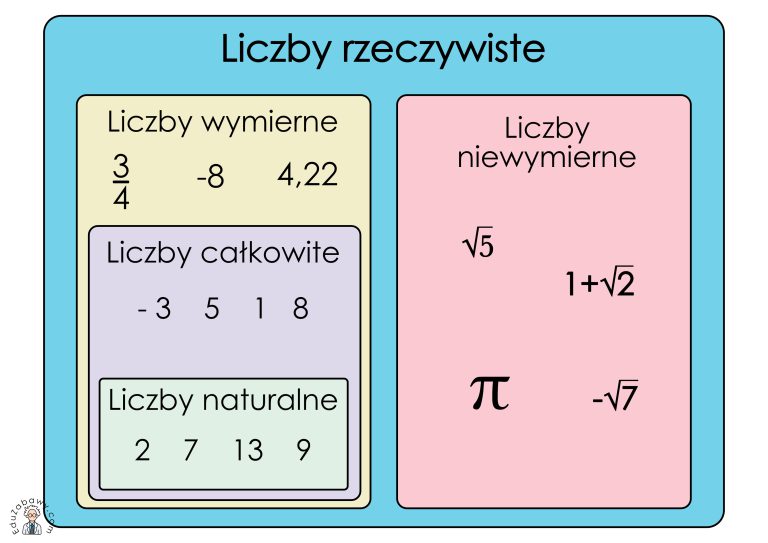
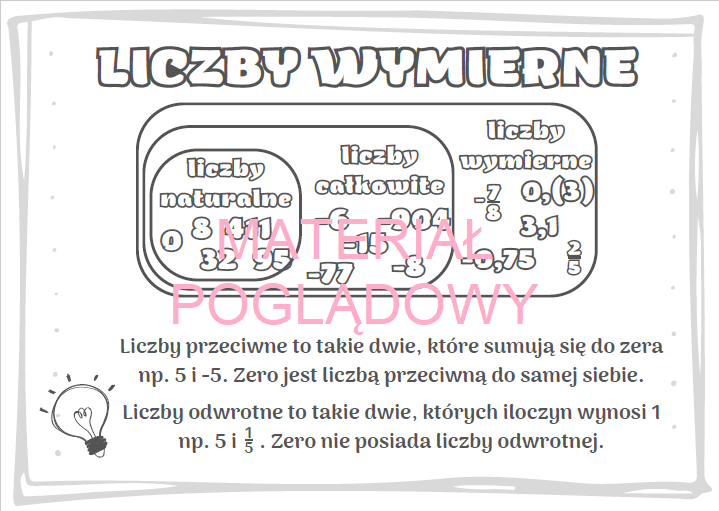
Co to właściwie są liczby wymierne?

Zacznijmy od początku. Liczba wymierna to każda liczba, którą można przedstawić w postaci ułamka a/b, gdzie a i b są liczbami całkowitymi, a b jest różne od zera. Innymi słowy, to liczby, które można zapisać jako iloraz dwóch liczb całkowitych. Pamiętaj, że zero nie może być mianownikiem! Przykładami liczb wymiernych są: 1/2, -3/4, 5, 0, -2.

Ważne jest, aby pamiętać, że każda liczba całkowita jest liczbą wymierną. Dlaczego? Bo każdą liczbę całkowitą możemy zapisać jako ułamek z mianownikiem równym 1. Na przykład, 5 to to samo co 5/1.

Przykłady liczb wymiernych:

• Ułamki zwykłe: 1/3, 7/8, -2/5
• Liczby całkowite: -5, 0, 12
• Ułamki dziesiętne skończone: 0.25, 1.75, -3.5
• Ułamki dziesiętne okresowe: 0.(3), 1.(6), -2.(142857)

Rodzaje zadań na sprawdzianie z liczb wymiernych

Sprawdziany z liczb wymiernych w 7 klasie zazwyczaj obejmują kilka typowych zadań. Oto one:

1. Zamiana ułamków zwykłych na dziesiętne i odwrotnie

Musisz umieć zamieniać ułamki zwykłe na dziesiętne i odwrotnie. Jak to zrobić?

Zamiana ułamka zwykłego na dziesiętny:

1. Podziel licznik przez mianownik. Na przykład, żeby zamienić 3/4 na ułamek dziesiętny, dzielimy 3 przez 4. Wynik to 0.75.
2. Jeśli wynik dzielenia jest nieskończony i okresowy, zapisujemy go z użyciem nawiasu wskazującego okres. Na przykład, 1/3 = 0.(3).

Zamiana ułamka dziesiętnego na zwykły:

1. Zapisz ułamek dziesiętny jako ułamek, gdzie w liczniku jest liczba bez przecinka, a w mianowniku 1 z tyloma zerami, ile jest cyfr po przecinku. Na przykład, 0.25 = 25/100.
2. Skróć ułamek do najprostszej postaci. W naszym przykładzie, 25/100 można skrócić do 1/4.

2. Działania na liczbach wymiernych

Kolejna ważna umiejętność to wykonywanie działań na liczbach wymiernych – dodawanie, odejmowanie, mnożenie i dzielenie. Pamiętaj o kolejności wykonywania działań!

Dodawanie i odejmowanie ułamków:

• Sprowadź ułamki do wspólnego mianownika.
• Dodaj lub odejmij liczniki, a mianownik pozostaw bez zmian.

Przykład: 1/2 + 1/4 = 2/4 + 1/4 = 3/4

Mnożenie ułamków:

• Pomnóż liczniki przez siebie.
• Pomnóż mianowniki przez siebie.

Przykład: 1/2 * 2/3 = (1*2) / (2*3) = 2/6 = 1/3

Dzielenie ułamków:

• Zamień dzielenie na mnożenie przez odwrotność drugiego ułamka.

Przykład: 1/2 : 2/3 = 1/2 * 3/2 = (1*3) / (2*2) = 3/4

Pamiętaj o znakach! Dodawanie i odejmowanie liczb ujemnych i dodatnich może być mylące. Przypomnij sobie zasady dotyczące znaków:

• Plus i plus daje plus.
• Minus i minus daje plus.
• Plus i minus daje minus.
• Minus i plus daje minus.

Na przykład: -3 + 5 = 2, -3 - 2 = -5, -3 * -2 = 6, -6 : 2 = -3

3. Porównywanie liczb wymiernych

Musisz wiedzieć, jak porównywać liczby wymierne, czyli określać, która liczba jest większa, mniejsza lub czy są równe. W przypadku ułamków, najłatwiej jest sprowadzić je do wspólnego mianownika lub zamienić na ułamki dziesiętne.

Przykład: Porównaj 1/3 i 1/4. Sprowadzamy do wspólnego mianownika: 1/3 = 4/12, 1/4 = 3/12. Widzimy, że 4/12 > 3/12, więc 1/3 > 1/4.

4. Upraszczanie wyrażeń algebraicznych zawierających liczby wymierne

Czasami na sprawdzianie pojawiają się wyrażenia algebraiczne z liczbami wymiernymi. Trzeba je uprościć, stosując zasady dotyczące kolejności wykonywania działań i redukcji wyrazów podobnych.

Przykład: 2x + 1/2 + x - 1/4 = 3x + 1/4 (po zredukowaniu wyrazów podobnych).

5. Zadania tekstowe

Nie obędzie się bez zadań tekstowych, w których trzeba zastosować wiedzę o liczbach wymiernych do rozwiązania konkretnego problemu. Kluczem jest uważne przeczytanie zadania, zrozumienie treści i wybranie odpowiednich działań.

Praktyczne wskazówki, jak przygotować się do sprawdzianu

Oto kilka praktycznych wskazówek, które pomogą Ci się dobrze przygotować:

1. Powtórz teorię: Przejrzyj definicje i zasady dotyczące liczb wymiernych. Upewnij się, że rozumiesz, co to jest ułamek, jak zamieniać ułamki zwykłe na dziesiętne i odwrotnie, jak wykonywać działania na liczbach wymiernych.
2. Rozwiąż zadania z podręcznika i zbioru zadań: Ćwiczenie czyni mistrza! Im więcej zadań rozwiążesz, tym lepiej utrwalisz wiedzę i nabierzesz pewności siebie. Skup się na różnych typach zadań.
3. Znajdź dodatkowe materiały online: W internecie znajdziesz mnóstwo darmowych materiałów edukacyjnych, takich jak arkusze ćwiczeń, testy online i filmy instruktażowe. Wykorzystaj je!
4. Poproś o pomoc: Jeśli masz problemy z jakimś zagadnieniem, nie bój się poprosić o pomoc nauczyciela, kolegę lub kogoś z rodziny. Wyjaśnienie trudnych kwestii przez kogoś innego może być bardzo pomocne.
5. Rozwiąż przykładowe sprawdziany: Poszukaj w internecie przykładowych sprawdzianów z liczb wymiernych dla 7 klasy. Rozwiązanie takiego sprawdzianu pozwoli Ci zorientować się, jakiego rodzaju zadania mogą się pojawić i na co zwrócić szczególną uwagę.
6. Zadbaj o odpowiedni odpoczynek: Dzień przed sprawdzianem odpocznij i dobrze się wyśpij. Wyspany umysł lepiej pracuje i łatwiej zapamiętuje informacje.
7. Przyjdź na sprawdzian punktualnie: Spóźnienie może wprowadzić niepotrzebny stres i utrudnić koncentrację.
8. Przeczytaj uważnie polecenia: Przed rozwiązaniem każdego zadania dokładnie przeczytaj polecenie i upewnij się, że je rozumiesz. Zastanów się, jakie informacje są podane w zadaniu i o co jesteś pytany.
9. Sprawdzaj swoje odpowiedzi: Po rozwiązaniu wszystkich zadań sprawdź swoje odpowiedzi. Upewnij się, że nie popełniłeś żadnych błędów rachunkowych lub logicznych.
10. Zachowaj spokój: Stres i nerwy mogą negatywnie wpłynąć na Twoje wyniki. Staraj się zachować spokój i skupić się na zadaniu. Pamiętaj, że nawet jeśli nie rozwiążesz wszystkich zadań, ważne jest, aby dać z siebie wszystko.

Typowe błędy na sprawdzianie z liczb wymiernych

Zwróć uwagę na najczęściej popełniane błędy, aby ich uniknąć:

• Błędy w znakach przy dodawaniu i odejmowaniu liczb ujemnych.
• Zapominanie o sprowadzeniu ułamków do wspólnego mianownika przed dodawaniem lub odejmowaniem.
• Błędy w kolejności wykonywania działań.
• Niewłaściwe zamienianie ułamków zwykłych na dziesiętne i odwrotnie.
• Brak skracania ułamków do najprostszej postaci.

Pamiętaj, praktyka czyni mistrza! Im więcej ćwiczysz, tym pewniej poczujesz się na sprawdzianie. Powodzenia!

Dodatkowe Materiały i Zasoby

W internecie znajdziesz wiele przydatnych zasobów, które pomogą Ci w nauce liczb wymiernych. Oto kilka propozycji:

• Khan Academy: Oferuje darmowe lekcje wideo i ćwiczenia z matematyki, w tym z liczb wymiernych.
• Matemaks: Polska strona internetowa z materiałami edukacyjnymi z matematyki, w tym z liczb wymiernych.
• Szalone Liczby: Kolejna polska strona z zadaniami i ćwiczeniami z matematyki.

Wykorzystaj te zasoby, aby uzupełnić swoją wiedzę i poćwiczyć rozwiązywanie zadań.

Na koniec – głowa do góry! Przygotowanie do sprawdzianu wymaga wysiłku, ale z dobrym planem i pozytywnym nastawieniem na pewno dasz radę! Powodzenia!