Liczby Wymierne Przyklady Klasa 6

Witaj w fascynującym świecie liczb wymiernych! Jeśli jesteś uczniem klasy 6, ten artykuł pomoże Ci zrozumieć, czym są liczby wymierne, jak je rozpoznawać i jak z nimi pracować. Przygotuj się na podróż pełną przykładów i praktycznych zastosowań.

Czym są Liczby Wymierne?

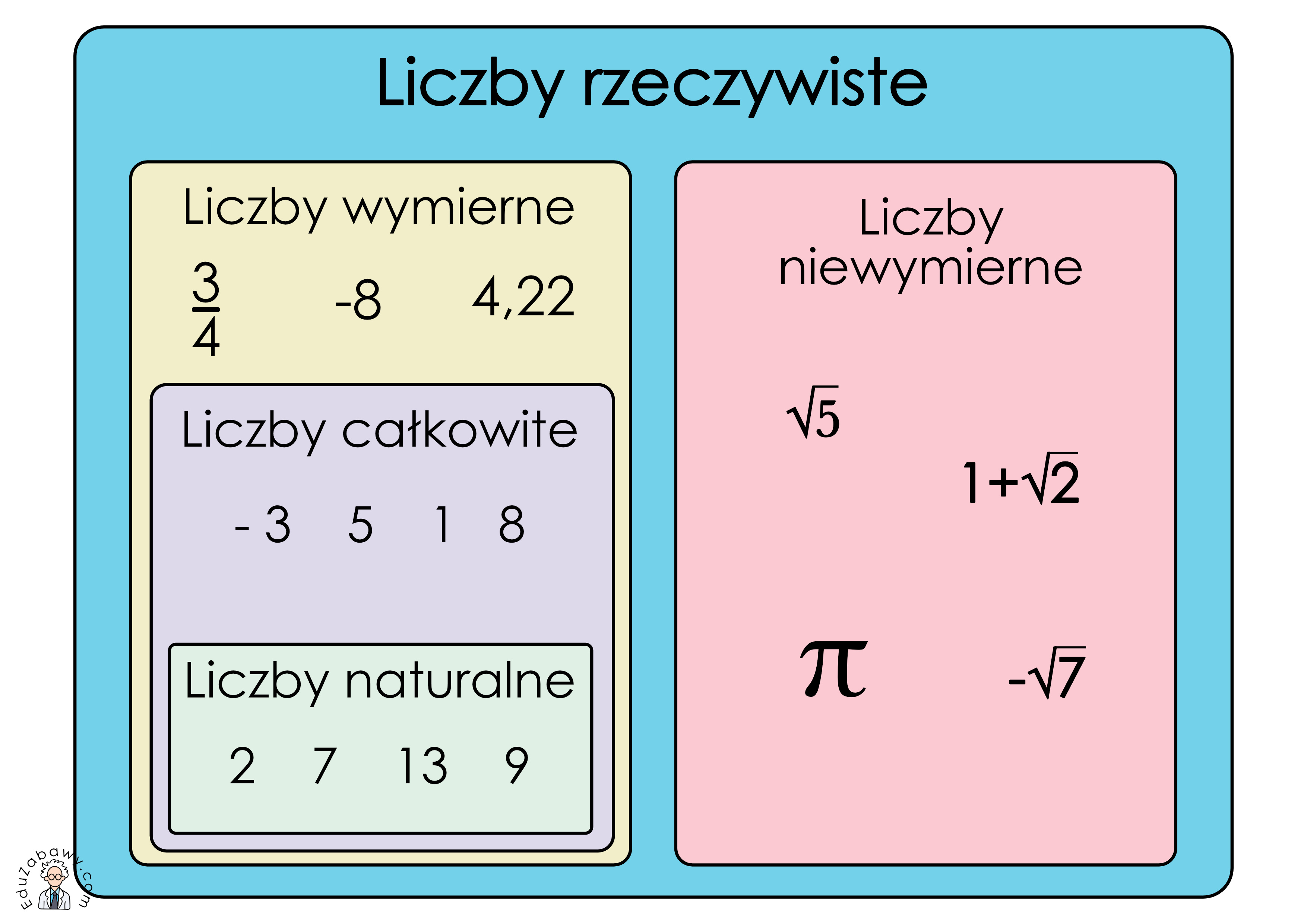
Liczba wymierna to każda liczba, którą można zapisać jako iloraz dwóch liczb całkowitych, gdzie mianownik jest różny od zera. Inaczej mówiąc, to liczba, którą da się przedstawić w postaci ułamka a/b, gdzie a i b są liczbami całkowitymi, a b ≠ 0.

Kluczowe cechy liczb wymiernych:

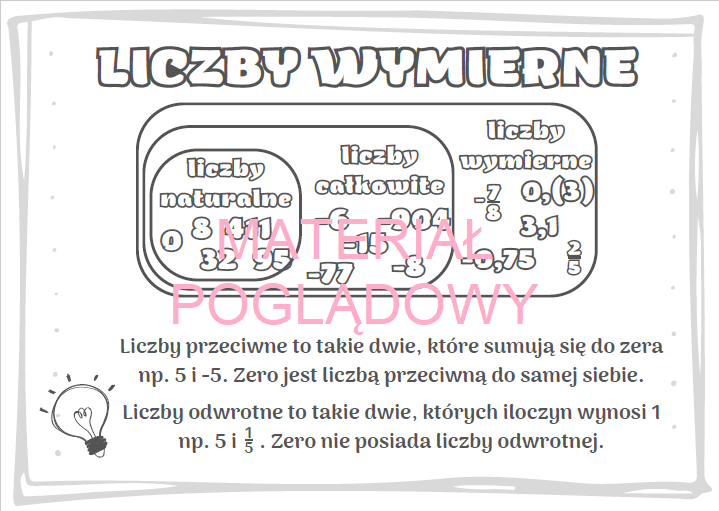
Można je zapisać jako ułamek zwykły (np. 1/2, 3/4, -5/7).
Mogą być liczbami całkowitymi (np. 5, -3, 0), ponieważ każdą liczbę całkowitą można zapisać jako ułamek o mianowniku 1 (np. 5 = 5/1).
Mogą być liczbami dziesiętnymi skończonymi (np. 0.25, 1.5, -3.75), ponieważ każdą liczbę dziesiętną skończoną można zamienić na ułamek zwykły (np. 0.25 = 1/4).
Mogą być liczbami dziesiętnymi okresowymi (np. 0.(3), 1.(6), -2.(142857)), ponieważ każdą liczbę dziesiętną okresową można zamienić na ułamek zwykły.

Ważne: Liczby, których nie można zapisać w postaci ułamka, nazywamy liczbami niewymiernymi (np. √2, π).

Przykłady Liczb Wymiernych

Żeby lepiej zrozumieć, spójrzmy na kilka konkretnych przykładów liczb wymiernych:

1/2 – Prosty ułamek, gdzie licznik to 1, a mianownik to 2.
3/4 – Kolejny ułamek, reprezentujący trzy czwarte całości.
-5/7 – Ułamek ujemny, pokazujący, że liczby wymierne mogą być również ujemne.
5 – Liczba całkowita, którą możemy zapisać jako 5/1.
0 – Zero, które możemy zapisać jako 0/1.
-3 – Liczba całkowita ujemna, którą możemy zapisać jako -3/1.
0.25 – Liczba dziesiętna skończona, którą możemy zapisać jako 1/4.
1.5 – Liczba dziesiętna skończona, którą możemy zapisać jako 3/2.
0.(3) – Liczba dziesiętna okresowa, gdzie 3 powtarza się w nieskończoność. Można ją zapisać jako 1/3.
2.(7) – Liczba dziesiętna okresowa, gdzie 7 powtarza się w nieskończoność. Można ją zapisać jako 25/9.

Liczby Dziesiętne i Ułamki Zwykłe

Jak już wspomnieliśmy, liczby wymierne mogą występować w postaci ułamków zwykłych i liczb dziesiętnych. Ważne jest, aby umieć zamieniać jedne na drugie.

Zamiana ułamka zwykłego na liczbę dziesiętną:

Aby zamienić ułamek zwykły na liczbę dziesiętną, należy podzielić licznik przez mianownik. Na przykład:

1/2 = 1 ÷ 2 = 0.5
3/4 = 3 ÷ 4 = 0.75
5/8 = 5 ÷ 8 = 0.625

Czasami wynik dzielenia daje liczbę dziesiętną skończoną, a czasami liczbę dziesiętną okresową.

Zamiana liczby dziesiętnej skończonej na ułamek zwykły:

Aby zamienić liczbę dziesiętną skończoną na ułamek zwykły, należy zapisać ją jako ułamek o mianowniku 10, 100, 1000, itd., w zależności od liczby cyfr po przecinku. Następnie ułamek należy uprościć, dzieląc licznik i mianownik przez ich największy wspólny dzielnik.

Na przykład:

0.25 = 25/100 = 1/4 (po uproszczeniu)
1.5 = 15/10 = 3/2 (po uproszczeniu)
0.125 = 125/1000 = 1/8 (po uproszczeniu)

Zamiana liczby dziesiętnej okresowej na ułamek zwykły:

Zamiana liczby dziesiętnej okresowej na ułamek zwykły jest nieco bardziej skomplikowana, ale postaram się to wyjaśnić w prosty sposób. Ograniczymy się do przykładów, które najczęściej pojawiają się w klasie 6.

Na przykład:

0.(3): Oznaczmy x = 0.(3). Wtedy 10x = 3.(3). Odejmując od tego x = 0.(3) otrzymujemy 9x = 3, czyli x = 3/9 = 1/3.
0.(6): Oznaczmy x = 0.(6). Wtedy 10x = 6.(6). Odejmując od tego x = 0.(6) otrzymujemy 9x = 6, czyli x = 6/9 = 2/3.

Działania na Liczbach Wymiernych

Teraz, gdy już wiesz, czym są liczby wymierne, możemy przejść do działań na nich. Podstawowe działania to dodawanie, odejmowanie, mnożenie i dzielenie.

Dodawanie i odejmowanie ułamków:

Aby dodać lub odjąć ułamki, muszą one mieć wspólny mianownik. Jeśli tak nie jest, należy je najpierw sprowadzić do wspólnego mianownika. Następnie dodajemy lub odejmujemy liczniki, a mianownik pozostaje bez zmian.

Na przykład:

1/2 + 1/4 = 2/4 + 1/4 = 3/4
3/5 - 1/5 = 2/5
1/3 + 1/6 = 2/6 + 1/6 = 3/6 = 1/2

Mnożenie ułamków:

Aby pomnożyć ułamki, mnożymy liczniki przez liczniki i mianowniki przez mianowniki.

Na przykład:

1/2 * 3/4 = (1 * 3) / (2 * 4) = 3/8
2/5 * 1/3 = (2 * 1) / (5 * 3) = 2/15

Dzielenie ułamków:

Aby podzielić ułamek przez ułamek, mnożymy pierwszy ułamek przez odwrotność drugiego ułamka. Odwrotność ułamka to ułamek, w którym zamieniono licznik z mianownikiem.

Na przykład:

1/2 ÷ 3/4 = 1/2 * 4/3 = (1 * 4) / (2 * 3) = 4/6 = 2/3
2/5 ÷ 1/3 = 2/5 * 3/1 = (2 * 3) / (5 * 1) = 6/5

Real-World Examples

Liczby wymierne otaczają nas z każdej strony! Oto kilka przykładów z życia codziennego:

Gotowanie: Przepisy często podają ilości składników w postaci ułamków (np. 1/2 szklanki mąki, 1/4 łyżeczki soli).
Mierzenie: Długość, waga, objętość – wszystko to często wyrażane jest za pomocą liczb wymiernych (np. 1.5 metra, 0.75 kg, 2.25 litra).
Zakupy: Ceny towarów często podawane są z użyciem liczb dziesiętnych (np. 2.99 zł, 5.50 zł).
Sport: Wyniki sportowe często zawierają ułamki lub liczby dziesiętne (np. czas biegu na 100 metrów: 12.5 sekundy).
Podział: Dzielenie pizzy na kawałki – każdy kawałek to ułamek całej pizzy (np. 1/8 pizzy).

Przykład z danymi: Wyobraź sobie, że masz 100 zł i chcesz kupić 2.5 kg jabłek, które kosztują 3.20 zł za kilogram. Koszt jabłek to 2.5 * 3.20 = 8 zł. Zostanie Ci 100 - 8 = 92 zł. Wszystkie te liczby są liczbami wymiernymi!

Praktyczne Ćwiczenia

Najlepszym sposobem na opanowanie liczb wymiernych jest praktyka. Spróbuj rozwiązać kilka zadań:

Zamień następujące ułamki na liczby dziesiętne: 1/5, 3/8, 7/20.
Zamień następujące liczby dziesiętne na ułamki zwykłe (uprość, jeśli to możliwe): 0.75, 1.2, 0.375.
Oblicz: 1/3 + 1/4, 2/5 - 1/10, 1/2 * 3/5, 3/4 ÷ 1/2.
Rozwiąż zadanie: Masz 2/3 tortu i chcesz podzielić go na 4 równe porcje. Jaką część całego tortu będzie stanowiła każda porcja?

Podsumowanie i Wezwanie do Działania

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, czym są liczby wymierne i jak z nimi pracować. Pamiętaj, że kluczem do sukcesu jest praktyka. Im więcej będziesz ćwiczyć, tym łatwiej będzie Ci radzić sobie z zadaniami z matematyki.

Teraz Twoja kolej! Weź kartkę i długopis, znajdź kilka zadań z liczbami wymiernymi i spróbuj je rozwiązać. Nie bój się popełniać błędów – to najlepszy sposób na naukę. Powodzenia!