Liczby Ujemne I Dodatnie Zadania

Liczby dodatnie i ujemne to fundamentalne pojęcia w matematyce, które wykraczają daleko poza szkolne ławki. Zrozumienie ich natury i umiejętność operowania nimi jest kluczowe nie tylko w rozwiązywaniu zadań, ale również w interpretacji otaczającej nas rzeczywistości. W tym artykule przyjrzymy się bliżej tym liczbom, omówimy ich właściwości, zastosowania oraz zaprezentujemy przykładowe zadania, które pozwolą lepiej zrozumieć ten temat.

Co to są Liczby Dodatnie i Ujemne?

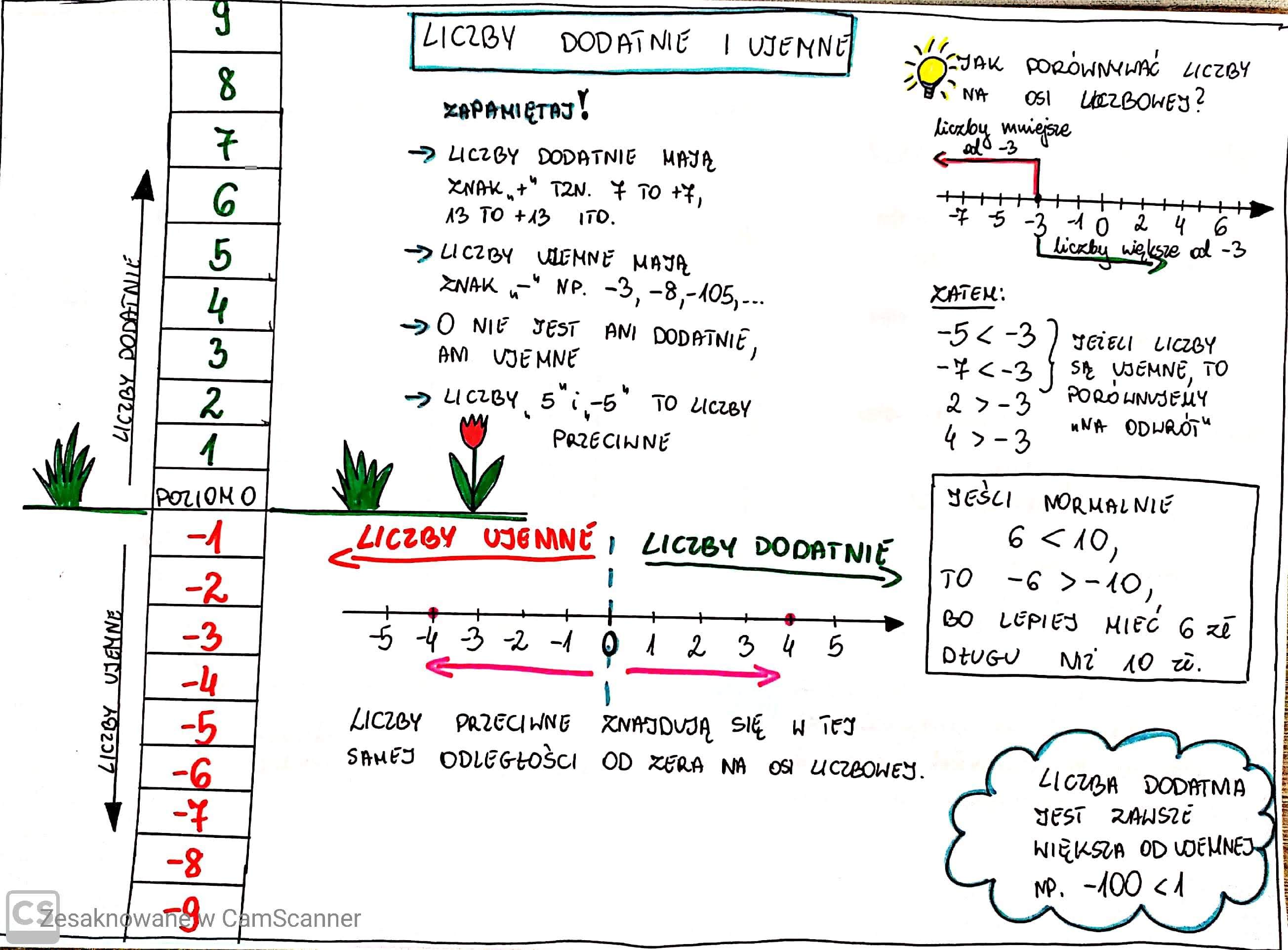
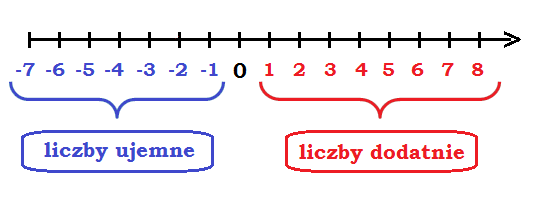
Liczby dodatnie to liczby większe od zera. Możemy je zapisać z plusem (+) przed liczbą (np. +5), ale znak ten często pomija się (np. 5). Liczby dodatnie reprezentują ilość, wzrost, zysk lub położenie powyżej punktu odniesienia. Na osi liczbowej znajdują się one po prawej stronie zera.

Liczby ujemne to liczby mniejsze od zera. Zawsze zapisujemy je ze znakiem minus (-) przed liczbą (np. -3). Liczby ujemne reprezentują brak, stratę, dług lub położenie poniżej punktu odniesienia. Na osi liczbowej znajdują się one po lewej stronie zera.

Zero (0) nie jest ani liczbą dodatnią, ani ujemną. Jest punktem neutralnym, oddzielającym liczby dodatnie od ujemnych.

Operacje na Liczbach Dodatnich i Ujemnych

Kluczowe jest zrozumienie, jak wykonywać operacje arytmetyczne (dodawanie, odejmowanie, mnożenie, dzielenie) na liczbach z różnymi znakami. Poniżej przedstawiamy zasady, które pomogą unikać błędów:

Dodawanie liczb o tym samym znaku: Dodajemy wartości bezwzględne liczb i przypisujemy wynikowi ten sam znak. Przykład: (+3) + (+5) = +8; (-2) + (-4) = -6
Dodawanie liczb o różnych znakach: Odejmujemy mniejszą wartość bezwzględną od większej wartości bezwzględnej. Wynikowi przypisujemy znak liczby o większej wartości bezwzględnej. Przykład: (+7) + (-3) = +4; (-9) + (+2) = -7
Odejmowanie liczb: Odejmowanie możemy zamienić na dodawanie liczby przeciwnej. Przykład: (+5) - (+2) = (+5) + (-2) = +3; (-3) - (-1) = (-3) + (+1) = -2
Mnożenie i dzielenie liczb o tym samym znaku: Wynik jest dodatni. Przykład: (+3) * (+2) = +6; (-4) / (-2) = +2
Mnożenie i dzielenie liczb o różnych znakach: Wynik jest ujemny. Przykład: (+5) * (-1) = -5; (-6) / (+3) = -2

Zadania z Liczbami Dodatnimi i Ujemnymi

Przejdźmy teraz do praktycznych przykładów zadań, które pomogą utrwalić zdobytą wiedzę:

Przykłady Zadań

Zadanie 1: Termometr wskazywał -5 stopni Celsjusza rano. W ciągu dnia temperatura wzrosła o 8 stopni Celsjusza. Ile stopni Celsjusza wskazuje termometr teraz?

Rozwiązanie: -5 + 8 = 3. Termometr wskazuje 3 stopnie Celsjusza.

Zadanie 2: Janek miał 20 zł długu. Oddał 12 zł. Ile długu mu jeszcze zostało?

Rozwiązanie: -20 + 12 = -8. Jankowi zostało jeszcze 8 zł długu.

Zadanie 3: Winda zjeżdża z 5 piętra o 7 pięter w dół. Na którym piętrze znajduje się winda?

Rozwiązanie: 5 - 7 = 5 + (-7) = -2. Winda znajduje się na piętrze -2 (czyli 2 piętra pod ziemią).

Zadanie 4: Oblicz: (-3) * (+4) - (-2)

Rozwiązanie: (-3) * (+4) = -12; -12 - (-2) = -12 + 2 = -10. Wynik to -10.

Zadanie 5: Znajdź liczbę przeciwną do liczby -(-5)

Rozwiązanie: Liczba przeciwna do -(-5) to liczba przeciwna do 5, czyli -5.

Trudniejsze Zadania

Spróbujmy teraz rozwiązać kilka bardziej skomplikowanych przykładów:

Zadanie 6: Oblicz wartość wyrażenia: [(-2) * 3 + 4] / (-1)

Rozwiązanie: (-2) * 3 = -6; -6 + 4 = -2; -2 / (-1) = 2. Wynik to 2.

Zadanie 7: Pewien przedsiębiorca miał na koncie -5000 zł. Zaciągnął kredyt w wysokości 10000 zł, a następnie spłacił 3000 zł. Jaki jest jego stan konta?

Rozwiązanie: -5000 + 10000 = 5000; 5000 - 3000 = 2000. Stan konta przedsiębiorcy to 2000 zł.

Zadanie 8: Rozwiąż równanie: x + (-3) = -7

Rozwiązanie: x = -7 - (-3) = -7 + 3 = -4. x = -4

Zadanie 9: Uprość wyrażenie: 2a - 3b + (-5a) + 2b

Rozwiązanie: 2a - 5a = -3a; -3b + 2b = -b. Wynik: -3a - b

Zadanie 10: Oblicz średnią arytmetyczną liczb: -8, 4, -2, 6

Rozwiązanie: (-8 + 4 + (-2) + 6) / 4 = (0) / 4 = 0. Średnia arytmetyczna wynosi 0.

Zastosowania Liczb Dodatnich i Ujemnych w Życiu Codziennym

Liczby dodatnie i ujemne mają szerokie zastosowanie w różnych dziedzinach życia. Oto kilka przykładów:

Finanse: Saldo konta bankowego (dodatnie - mamy pieniądze, ujemne - debet), zyski i straty przedsiębiorstw, notowania giełdowe (wzrosty i spadki), oprocentowanie kredytów (koszt pożyczki).
Temperatura: Stopnie Celsjusza i Fahrenheita (poniżej zera), zmiany temperatur (wzrost lub spadek).
Geografia: Wysokość nad poziomem morza (dodatnia) i głębokość poniżej poziomu morza (ujemna).
Sport: Różnica bramek w piłce nożnej (dodatnia - więcej goli strzelonych, ujemna - więcej goli straconych), punktacja w niektórych grach (punkty dodatnie i karne).
Informatyka: Reprezentacja danych (np. współrzędne na ekranie, zmiany wartości zmiennych).

Przykłady z Danymi

Spójrzmy na kilka przykładów opartych na hipotetycznych danych:

Przykład 1: Firma XYZ w pierwszym kwartale zanotowała stratę w wysokości 15 000 zł (-15 000 zł), a w drugim kwartale zysk w wysokości 25 000 zł (+25 000 zł). Jaki jest łączny wynik finansowy firmy po dwóch kwartałach? Rozwiązanie: -15 000 + 25 000 = 10 000 zł. Firma ma 10 000 zł zysku.
Przykład 2: Temperatura w Krakowie o godzinie 6:00 wynosiła -2 stopnie Celsjusza. Do godziny 12:00 temperatura wzrosła o 7 stopni Celsjusza, a następnie do godziny 18:00 spadła o 3 stopnie Celsjusza. Jaka temperatura była o godzinie 18:00? Rozwiązanie: -2 + 7 = 5; 5 - 3 = 2. Temperatura o 18:00 wynosiła 2 stopnie Celsjusza.

Podsumowanie

Zrozumienie liczb dodatnich i ujemnych jest fundamentalne dla dalszej nauki matematyki i jej zastosowań w życiu codziennym. Opanowanie zasad operowania tymi liczbami pozwala na poprawne rozwiązywanie zadań i interpretację informacji. Pamiętaj o ćwiczeniach i regularnym rozwiązywaniu zadań, aby utrwalić zdobytą wiedzę. Nie bój się pytać i szukać wyjaśnień, gdy napotkasz trudności. Matematyka, choć czasem wymagająca, może być fascynującą i przydatną dziedziną.

Kontynuuj swoją edukację matematyczną! Sięgnij po dodatkowe materiały, rozwiązuj więcej zadań i obserwuj, jak liczby dodatnie i ujemne otaczają Cię w codziennym życiu. Zrozumienie ich to krok do lepszego rozumienia świata.