Liczby Podzielne Przez 2 I 3

Czy kiedykolwiek zastanawiałeś się, jak niektóre liczby zdają się mieć magiczne właściwości? Takie, które bez problemu dzielą się na równe części, bez żadnych resztek? Matematyka, choć czasem wydaje się abstrakcyjna, otacza nas z każdej strony, a zrozumienie podstawowych zasad, jak choćby podzielności przez 2 i 3, może otworzyć nam oczy na otaczający świat i ułatwić codzienne życie.

Wielu z nas, słysząc hasło "matematyka", odczuwa pewien dyskomfort. Może to wynikać z przykrych wspomnień ze szkoły, trudnych zadań domowych czy po prostu przekonania, że "to nie dla mnie". Ale uwierz mi, zrozumienie koncepcji podzielności nie wymaga geniuszu! To umiejętność, którą każdy może opanować, a korzyści z niej płynące są zaskakująco szerokie.

Dlaczego Warto Znać Zasady Podzielności?

Zastanówmy się, gdzie w życiu codziennym możemy wykorzystać wiedzę o podzielności liczb. Okazuje się, że w wielu, nawet nieoczywistych sytuacjach!

Podział obowiązków: Wyobraź sobie, że masz do podziału 12 ciasteczek pomiędzy 3 osoby. Wiedząc, że 12 jest podzielne przez 3, od razu wiesz, że każdy dostanie po 4 ciasteczka. Proste, prawda?
Planowanie wydatków: Masz 360 złotych i chcesz rozłożyć je na 6 miesięcy. Sprawdzając, czy 360 jest podzielne przez 6, łatwo obliczysz, ile możesz wydać miesięcznie.
Organizowanie wydarzeń: Planujesz przyjęcie i chcesz rozstawić stoły w równych rzędach. Znajomość podzielności pomoże Ci określić, ile stołów możesz ustawić w każdym rzędzie, aby wszystko wyglądało estetycznie.
Programowanie: W informatyce znajomość podzielności jest kluczowa w algorytmach optymalizacyjnych i analizie danych.

Podzielność Przez 2: Proste Jak 1, 2, 3...

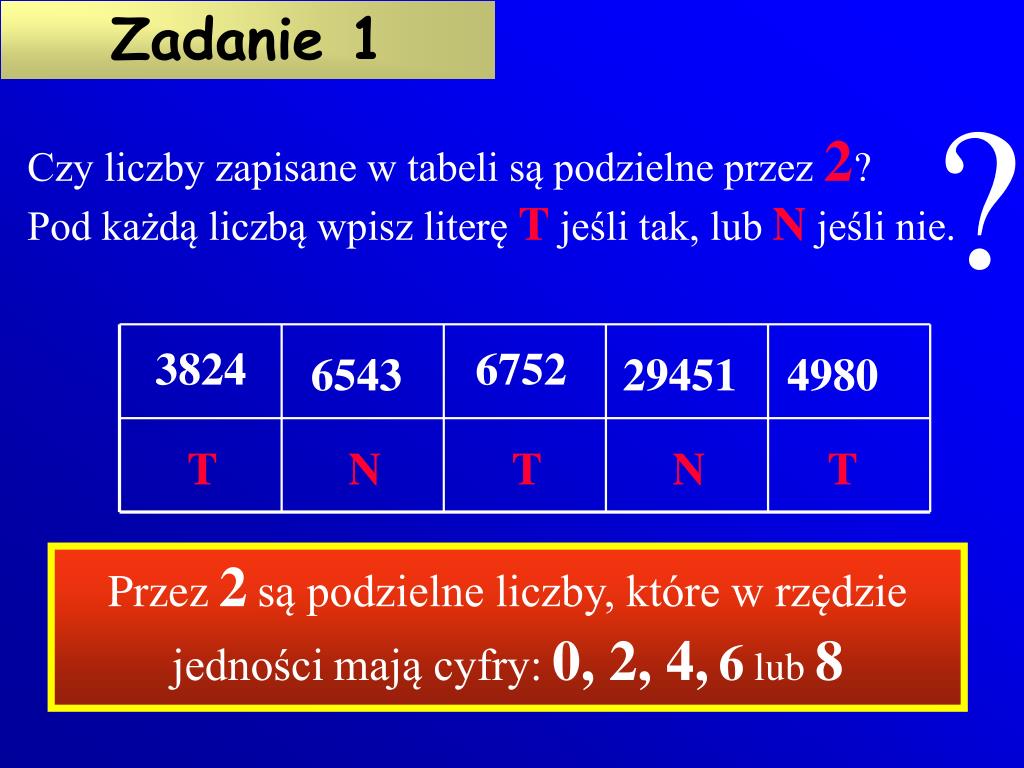
Najprostsza zasada dotyczy podzielności przez 2. Liczba jest podzielna przez 2, jeśli jej ostatnia cyfra jest parzysta (0, 2, 4, 6 lub 8). To naprawdę takie proste!

Przykłady:

12 - podzielne przez 2, bo ostatnia cyfra to 2.
346 - podzielne przez 2, bo ostatnia cyfra to 6.
1578 - podzielne przez 2, bo ostatnia cyfra to 8.
999 - niepodzielne przez 2, bo ostatnia cyfra to 9.

Podzielność Przez 3: Dodajemy Cyfry!

Zasada podzielności przez 3 jest nieco bardziej wymagająca, ale równie łatwa do zapamiętania. Liczba jest podzielna przez 3, jeśli suma jej cyfr jest podzielna przez 3.

Przykłady:

12 - 1 + 2 = 3. 3 jest podzielne przez 3, więc 12 jest podzielne przez 3.
27 - 2 + 7 = 9. 9 jest podzielne przez 3, więc 27 jest podzielne przez 3.
123 - 1 + 2 + 3 = 6. 6 jest podzielne przez 3, więc 123 jest podzielne przez 3.
456 - 4 + 5 + 6 = 15. 1 + 5 = 6. 6 jest podzielne przez 3, więc 456 jest podzielne przez 3.
789 - 7 + 8 + 9 = 24. 2 + 4 = 6. 6 jest podzielne przez 3, więc 789 jest podzielne przez 3.
101 - 1 + 0 + 1 = 2. 2 nie jest podzielne przez 3, więc 101 nie jest podzielne przez 3.

Liczby Podzielne Przez 2 I 3: Kiedy Mamy Do Czynienia Z "Super Liczbą"?

Skoro już znamy zasady podzielności przez 2 i 3, możemy przejść do liczb, które są podzielne przez oba te czynniki. Liczba jest podzielna zarówno przez 2, jak i przez 3, jeśli spełnia obie zasady jednocześnie. Oznacza to, że:

Ostatnia cyfra liczby musi być parzysta (0, 2, 4, 6 lub 8).
Suma cyfr liczby musi być podzielna przez 3.

Spójrzmy na kilka przykładów:

6 - Ostatnia cyfra (6) jest parzysta, a suma cyfr (6) jest podzielna przez 3. Zatem 6 jest podzielne przez 2 i 3.
12 - Ostatnia cyfra (2) jest parzysta, a suma cyfr (1 + 2 = 3) jest podzielna przez 3. Zatem 12 jest podzielne przez 2 i 3.
18 - Ostatnia cyfra (8) jest parzysta, a suma cyfr (1 + 8 = 9) jest podzielna przez 3. Zatem 18 jest podzielne przez 2 i 3.
24 - Ostatnia cyfra (4) jest parzysta, a suma cyfr (2 + 4 = 6) jest podzielna przez 3. Zatem 24 jest podzielne przez 2 i 3.
30 - Ostatnia cyfra (0) jest parzysta, a suma cyfr (3 + 0 = 3) jest podzielna przez 3. Zatem 30 jest podzielne przez 2 i 3.
15 - Suma cyfr (1+5 = 6) jest podzielna przez 3, ale ostatnia cyfra (5) nie jest parzysta. Zatem 15 jest podzielne przez 3 ale nie przez 2.
20 - Ostatnia cyfra (0) jest parzysta, ale suma cyfr (2 + 0 = 2) nie jest podzielna przez 3. Zatem 20 jest podzielne przez 2 ale nie przez 3.

Dlaczego To Działa?

Możesz się zastanawiać, dlaczego te zasady działają. To wynika z matematycznych właściwości systemu dziesiętnego, w którym zapisujemy liczby. Bez wchodzenia w szczegóły techniczne, można powiedzieć, że zasada podzielności przez 2 opiera się na tym, że każda liczba parzysta jest wielokrotnością 2, a zasada podzielności przez 3 wynika z tego, że różnica między liczbą a sumą jej cyfr jest zawsze podzielna przez 3. Zatem, jeśli suma cyfr jest podzielna przez 3, to i sama liczba jest podzielna przez 3.

Adresowanie Kontrargumentów: "To Mi Się Nigdy Nie Przyda!"

Zdarza się, że ludzie podważają praktyczne zastosowanie wiedzy o podzielności, twierdząc, że w dobie kalkulatorów i komputerów takie umiejętności są zbędne. To prawda, że w wielu sytuacjach możemy szybko sprawdzić podzielność za pomocą technologii. Jednak:

Znajomość zasad podzielności rozwija logiczne myślenie i umiejętność rozwiązywania problemów.
Pomaga w szybkim szacowaniu i weryfikacji poprawności wyników obliczeń.
Daje satysfakcję z rozumienia otaczającego nas świata i praw matematyki.
Może być przydatna w sytuacjach awaryjnych, gdy nie mamy dostępu do kalkulatora.

Poza tym, wiedza o podzielności jest fundamentem do zrozumienia bardziej zaawansowanych zagadnień matematycznych, takich jak liczby pierwsze, rozkład na czynniki pierwsze czy cechy podzielności przez inne liczby.

Rozwiązania, Nie Tylko Problemy: Jak Ćwiczyć Podzielność?

Najlepszym sposobem na opanowanie zasad podzielności jest praktyka. Oto kilka propozycji:

Zabawa w liczby: Wybierz losową liczbę i spróbuj ustalić, czy jest podzielna przez 2 i 3, stosując poznane zasady.
Ćwiczenia online: W Internecie znajdziesz wiele interaktywnych ćwiczeń i quizów, które pomogą Ci w utrwaleniu wiedzy.
Zadania z podręcznika: Wykorzystaj zadania ze szkolnego podręcznika do matematyki, aby poćwiczyć rozwiązywanie problemów związanych z podzielnością.
Zastosowanie w życiu codziennym: Szukaj okazji do wykorzystania wiedzy o podzielności w codziennych sytuacjach, takich jak podział obowiązków, planowanie wydatków czy organizowanie wydarzeń.
Ucz innych: Wytłumacz zasady podzielności komuś innemu. To najlepszy sposób na utrwalenie wiedzy i przekonanie się, czy naprawdę ją rozumiesz.

Pamiętaj, że każdy może nauczyć się matematyki! Kluczem jest cierpliwość, systematyczność i pozytywne nastawienie.

Podsumowanie

Zrozumienie zasad podzielności przez 2 i 3 to cenne narzędzie, które może ułatwić nam życie i rozwinąć nasze umiejętności logicznego myślenia. Nie bój się matematyki! Potraktuj ją jak przygodę i odkrywaj jej fascynujący świat krok po kroku. Zaczynając od podstaw, możesz dojść bardzo daleko.

Czy teraz, mając tę wiedzę, spróbujesz znaleźć liczby w swoim otoczeniu, które są podzielne zarówno przez 2, jak i przez 3? I czy zastanowisz się, jak możesz wykorzystać tę wiedzę w swoim codziennym życiu?