Liczby Naturalne Klasa 5 Sprawdzian

Witajcie, młodzi matematycy! Przygotowujecie się do sprawdzianu z liczb naturalnych w 5 klasie? Świetnie! Ten temat to podstawa, na której zbudujemy całą naszą matematyczną wiedzę. Pomyślcie o liczbach naturalnych jak o cegłach, z których wznosimy budynki – im lepiej je poznamy, tym solidniejsza będzie nasza budowla!

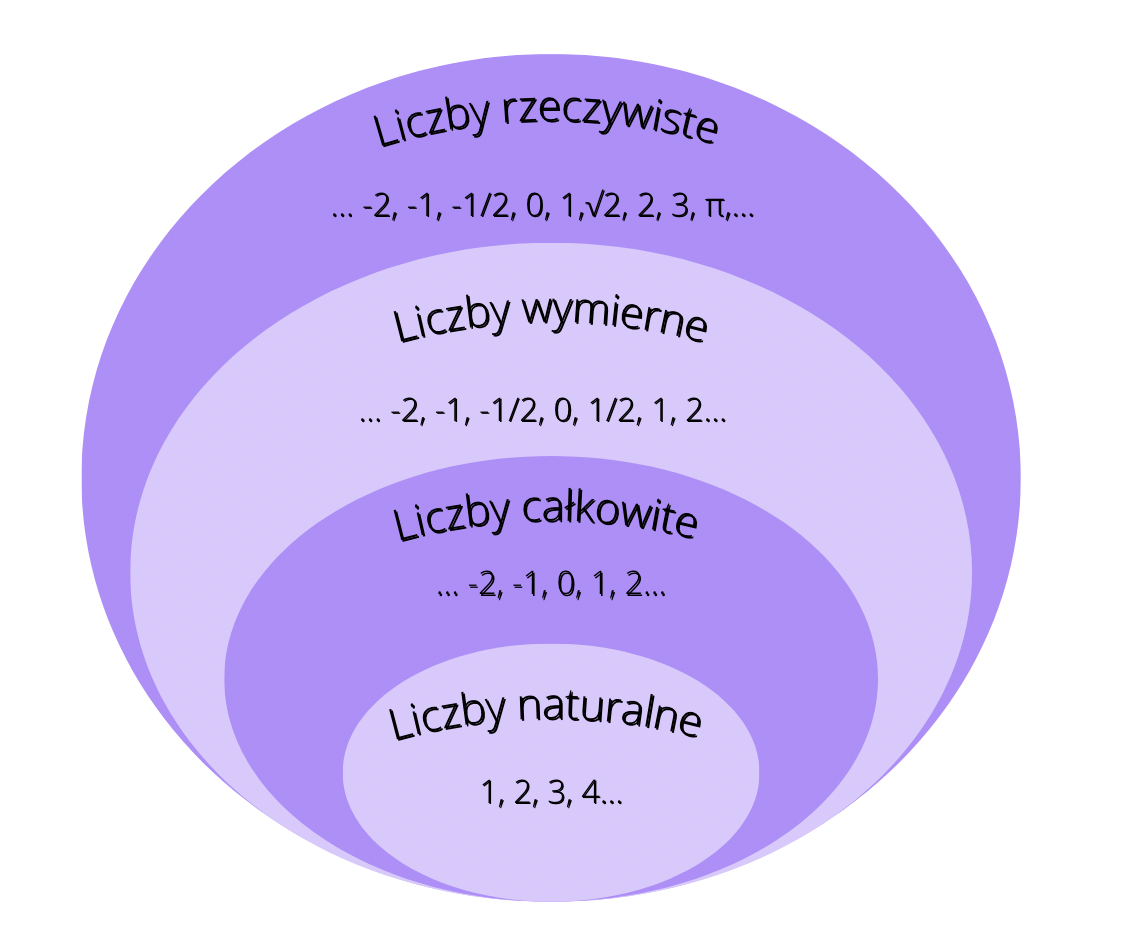
Co to są liczby naturalne?

Liczby naturalne to po prostu liczby, którymi liczymy przedmioty. Zaczynamy od 1, potem 2, 3, 4... i tak dalej, w nieskończoność. Wyobraźcie sobie, że macie koszyk jabłek. Możecie mieć jedno jabłko (1), dwa jabłka (2), pięć jabłek (5), a nawet 100 jabłek (100)! Liczby 1, 2, 5, 100 to liczby naturalne.

Ważne: Zero (0) zazwyczaj zaliczamy do liczb naturalnych, choć nie zawsze. To zależy od podręcznika i tego, co ustali wasz nauczyciel. Zapamiętajcie to dobrze! Pomyśl o zerze jak o pustym koszyku – nie ma w nim żadnych jabłek.

Czyli, zbiór liczb naturalnych możemy zapisać tak: {1, 2, 3, 4, 5, 6...} lub (jeśli zero zalicza się) {0, 1, 2, 3, 4, 5, 6...}.

Co **NIE** jest liczbą naturalną? Na pewno nie ułamki (np. 1/2), liczby ujemne (np. -3) czy liczby dziesiętne (np. 2,5). Wyobraźcie sobie, że macie tylko całe jabłka. Nie możecie mieć "pół jabłka", więc 1/2 nie jest liczbą naturalną w tym naszym przykładzie. Podobnie, nie możecie mieć "-3 jabłek" – po prostu nie da się tego fizycznie zrobić!

Działania na liczbach naturalnych

Skoro już wiemy, czym są liczby naturalne, zobaczmy, co możemy z nimi robić. Mamy cztery podstawowe działania:

Dodawanie

Dodawanie to łączenie. Jeśli masz 3 cukierki, a dostaniesz od kolegi 2 cukierki, to razem masz 3 + 2 = 5 cukierków. Dodawanie możemy sobie wyobrazić jako dołączanie elementów do grupy. Można to zobaczyć na osi liczbowej – zaczynamy od jednej liczby i przesuwamy się w prawo o tyle, ile wynosi druga liczba.

Odejmowanie

Odejmowanie to zabieranie. Jeśli miałeś 5 ciasteczek i zjadłeś 2, to zostało ci 5 - 2 = 3 ciasteczka. Odejmowanie to tak, jakby z grupy elementów coś usunąć. Na osi liczbowej, odejmowanie to przesuwanie się w lewo.

Pamiętaj: W odejmowaniu od większej liczby odejmujemy mniejszą (przynajmniej na tym etapie nauki!). Nie możemy od 2 jabłek odjąć 5, bo po prostu nie mamy wystarczająco dużo jabłek!

Mnożenie

Mnożenie to dodawanie tego samego kilka razy. Jeśli masz 4 paczki po 3 kredki w każdej, to razem masz 4 * 3 = 12 kredek. Mnożenie możemy wyobrazić sobie jako tworzenie grup o takiej samej liczbie elementów. Wyobraź sobie tabliczkę mnożenia jako siatkę – na przecięciu wiersza i kolumny masz wynik mnożenia.

Dzielenie

Dzielenie to rozdzielanie na równe części. Jeśli masz 12 cukierków i chcesz je rozdać równo trzem kolegom, to każdy dostanie 12 / 3 = 4 cukierki. Dzielenie to tak, jakbyśmy mieli jakąś całość i chcieli ją sprawiedliwie podzielić. Możemy sobie wyobrazić, że mamy stos monet i układamy z nich równe rzędy – liczba monet w rzędzie to wynik dzielenia.

Ważne: Pamiętaj o kolejności wykonywania działań! Najpierw mnożenie i dzielenie (od lewej do prawej), potem dodawanie i odejmowanie (od lewej do prawej). Można zapamiętać to dzięki mnemotechnice: "Mój Drogi Wujku, Daj Obiadów".

Dzielniki i Wielokrotności

To bardzo ważne pojęcia! Zrozumienie ich ułatwi wam rozwiązywanie wielu zadań.

Dzielniki

Dzielnik danej liczby to liczba, przez którą dana liczba dzieli się bez reszty. Na przykład, dzielnikami liczby 12 są: 1, 2, 3, 4, 6 i 12. Sprawdźmy: 12 / 1 = 12, 12 / 2 = 6, 12 / 3 = 4, 12 / 4 = 3, 12 / 6 = 2, 12 / 12 = 1. Widzimy, że wszystkie te dzielenia dają wynik bez reszty.

Spróbujmy wizualizacji. Wyobraź sobie, że masz 12 klocków. Możesz je ułożyć w jeden długi rząd (1 x 12), dwa rzędy po 6 klocków (2 x 6), trzy rzędy po 4 klocki (3 x 4), cztery rzędy po 3 klocki (4 x 3), sześć rzędów po 2 klocki (6 x 2) lub dwanaście rzędów po jednym klocku (12 x 1). W każdym z tych układów, liczba klocków w rzędzie jest dzielnikiem liczby 12.

Wielokrotności

Wielokrotność danej liczby to wynik mnożenia tej liczby przez jakąś liczbę naturalną. Na przykład, wielokrotnościami liczby 3 są: 3, 6, 9, 12, 15, 18... (3 * 1 = 3, 3 * 2 = 6, 3 * 3 = 9, 3 * 4 = 12, i tak dalej). Inaczej mówiąc, to wszystkie liczby, które dzielą się przez daną liczbę bez reszty.

Wyobraź sobie, że skaczesz po osi liczbowej co 3 kroki. Zaczynasz od 0, potem skaczesz na 3, potem na 6, potem na 9... Każdy punkt, na który skoczysz, to wielokrotność liczby 3.

Jak przygotować się do sprawdzianu?

* Powtórz definicje: Upewnij się, że rozumiesz, czym są liczby naturalne, dzielniki i wielokrotności.

* Rozwiązuj zadania: Im więcej zadań rozwiążesz, tym lepiej utrwalisz wiedzę. Zacznij od prostych, a potem przejdź do trudniejszych.

* Wykorzystaj wizualizacje: Rysuj osie liczbowe, używaj klocków, wyobrażaj sobie sytuacje z życia codziennego. To pomaga zrozumieć matematykę!

* Poproś o pomoc: Jeśli masz problem z jakimś zadaniem, nie bój się zapytać nauczyciela, rodziców lub kolegów. Lepiej rozwiać wątpliwości przed sprawdzianem.

Pamiętaj, że matematyka to nie tylko liczby i wzory, ale też logiczne myślenie i rozwiązywanie problemów. Powodzenia na sprawdzianie!