Liczby Naturalne I Ulamki Klasa 6 Gwo

Czy kiedykolwiek zastanawialiście się, jak dzielimy pizzę pomiędzy przyjaciół, albo jak liczymy ilość cukierków w paczce? Odpowiedzi na te pytania kryją się w fascynującym świecie liczb naturalnych i ułamków zwykłych. Ten artykuł, skierowany do uczniów klasy 6, pomoże Wam zrozumieć te fundamentalne pojęcia matematyczne, które towarzyszą nam na co dzień. Zobaczycie, że matematyka wcale nie musi być trudna, a wręcz przeciwnie – może być ciekawa i przydatna!
Liczymy razem: Liczby naturalne
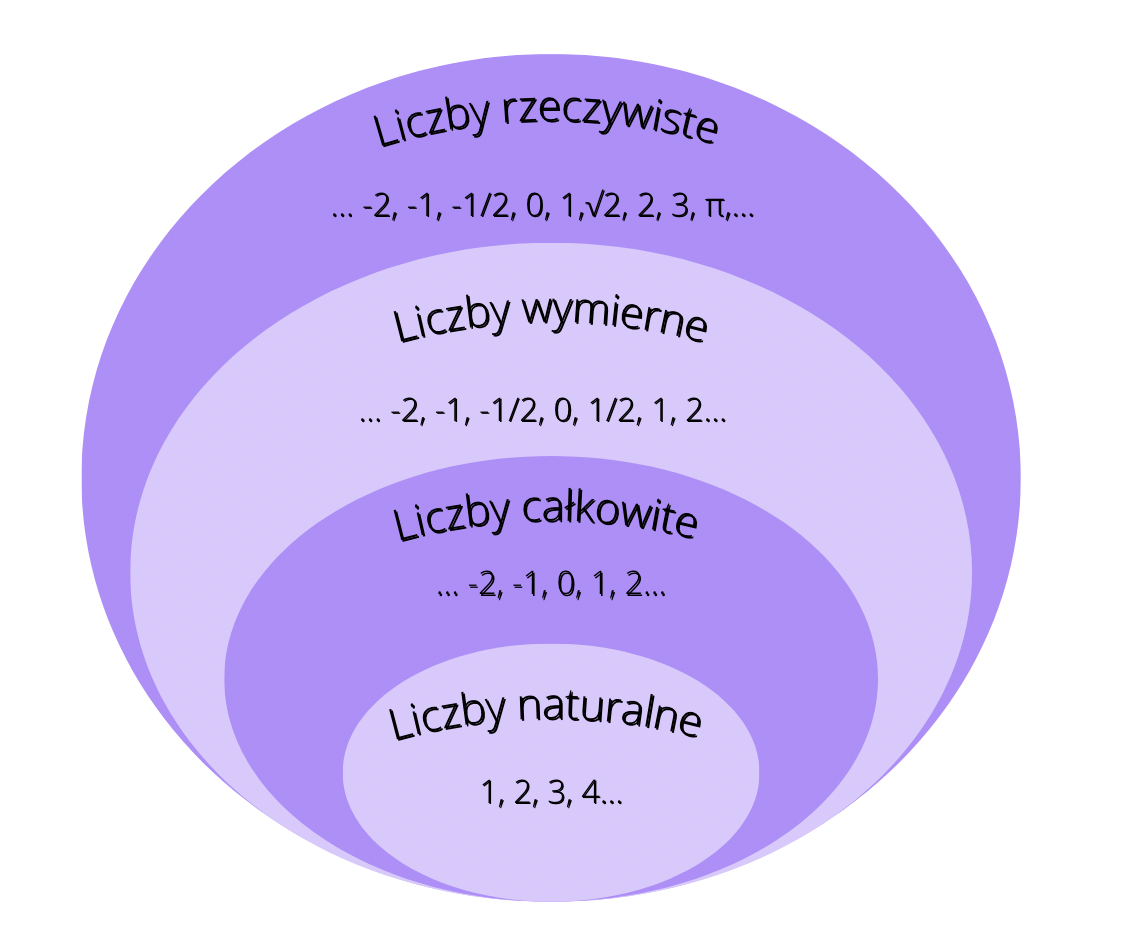
Liczby naturalne to po prostu liczby, których używamy do liczenia. Zaczynają się od 1 i rosną w nieskończoność: 1, 2, 3, 4, 5, i tak dalej. Używamy ich do określania ilości przedmiotów, np. "Mam 3 jabłka" albo "W klasie jest 25 uczniów".
Co możemy robić z liczbami naturalnymi?
Z liczbami naturalnymi możemy wykonywać różne działania:
- Dodawanie: Łączenie dwóch lub więcej liczb, np. 2 + 3 = 5. Myślimy o tym jak o dodawaniu jabłek do koszyka. Jeśli masz 2 jabłka i dodasz 3, to będziesz miał ich 5.
- Odejmowanie: Odejmowanie jednej liczby od drugiej, np. 5 - 2 = 3. To tak jakbyś zjadał jabłka z koszyka. Jeśli masz 5 jabłek i zjesz 2, to zostaną Ci 3.
- Mnożenie: Szybkie dodawanie tej samej liczby wiele razy, np. 2 x 3 = 6. To jak posiadanie kilku koszyków z tą samą liczbą jabłek. Jeśli masz 3 koszyki, a w każdym są 2 jabłka, to w sumie masz 6 jabłek.
- Dzielenie: Podział jednej liczby na równe części, np. 6 : 2 = 3. To jak dzielenie jabłek pomiędzy przyjaciół. Jeśli masz 6 jabłek i chcesz je rozdać równo pomiędzy 2 osoby, to każda osoba dostanie 3 jabłka.
Pamiętajcie! Dzielenie przez 0 nie jest możliwe! Nie można podzielić niczego na zero części.
Ułamki zwykłe: Dzielimy sprawiedliwie
Często zdarza się, że nie możemy podzielić czegoś na całe liczby. Wtedy wkraczają do akcji ułamki zwykłe. Ułamek zwykły to część całości. Zapisujemy go jako dwie liczby oddzielone kreską ułamkową:
licznik⁄mianownik
- Licznik: Mówi nam, ile części mamy.
- Mianownik: Mówi nam, na ile równych części podzielona jest całość.
Na przykład, jeśli podzielimy pizzę na 8 równych kawałków i zjemy 3 z nich, to zjemy 3⁄8 pizzy. Mianownik (8) mówi nam, na ile kawałków podzielona jest pizza, a licznik (3) mówi nam, ile kawałków zjedliśmy.
Rodzaje ułamków
Ułamki dzielimy na:
- Ułamki właściwe: Licznik jest mniejszy niż mianownik, np. 1⁄2, 3⁄4, 5⁄6. Ułamek właściwy jest zawsze mniejszy niż 1.
- Ułamki niewłaściwe: Licznik jest większy lub równy mianownikowi, np. 5⁄2, 7⁄4, 6⁄6. Ułamek niewłaściwy jest większy lub równy 1.
- Liczby mieszane: Składają się z liczby całkowitej i ułamka właściwego, np. 21⁄2, 13⁄4. Oznaczają one całość i jeszcze jakąś część. 21⁄2 to to samo co 2 całe i pół.
Zamiana ułamków niewłaściwych na liczby mieszane i odwrotnie
Zamiana ułamka niewłaściwego na liczbę mieszaną:
Dzielimy licznik przez mianownik. Wynik dzielenia to liczba całkowita, a reszta z dzielenia to licznik w ułamku właściwym. Mianownik pozostaje bez zmian.
Przykład: 7⁄3
7 : 3 = 2 reszty 1
Czyli 7⁄3 = 21⁄3
Zamiana liczby mieszanej na ułamek niewłaściwy:
Mnożymy liczbę całkowitą przez mianownik i dodajemy do tego licznik. Wynik to licznik w ułamku niewłaściwym. Mianownik pozostaje bez zmian.
Przykład: 32⁄5
(3 x 5) + 2 = 17
Czyli 32⁄5 = 17⁄5
Rozszerzanie i skracanie ułamków
Rozszerzanie ułamków: Polega na pomnożeniu licznika i mianownika przez tę samą liczbę różną od zera. Rozszerzanie nie zmienia wartości ułamka, tylko jego wygląd.
Przykład: 1⁄2 = 1 x 2⁄2 x 2 = 2⁄4
Skracanie ułamków: Polega na podzieleniu licznika i mianownika przez ten sam dzielnik różny od zera. Skracanie również nie zmienia wartości ułamka, tylko jego wygląd.
Przykład: 4⁄8 = 4 : 4⁄8 : 4 = 1⁄2
Pamiętajcie! Ułamek, którego nie da się już skrócić, nazywamy ułamkiem nieskracalnym.
Porównywanie ułamków
Aby porównać ułamki, musimy sprowadzić je do wspólnego mianownika, czyli takiego samego mianownika. Następnie porównujemy liczniki. Ten ułamek, który ma większy licznik, jest większy.
Przykład: Porównaj ułamki 2⁄3 i 3⁄4
Wspólny mianownik dla 3 i 4 to 12.
2⁄3 = 2 x 4⁄3 x 4 = 8⁄12
3⁄4 = 3 x 3⁄4 x 3 = 9⁄12
Ponieważ 9⁄12 > 8⁄12, to 3⁄4 > 2⁄3
Działania na ułamkach zwykłych
Dodawanie i odejmowanie ułamków o tych samych mianownikach: Dodajemy (lub odejmujemy) liczniki, a mianownik pozostaje bez zmian.
Przykład: 2⁄5 + 1⁄5 = 2 + 1⁄5 = 3⁄5
Dodawanie i odejmowanie ułamków o różnych mianownikach: Najpierw sprowadzamy ułamki do wspólnego mianownika, a następnie dodajemy (lub odejmujemy) liczniki.
Przykład: 1⁄2 + 1⁄3
Wspólny mianownik dla 2 i 3 to 6.
1⁄2 = 3⁄6
1⁄3 = 2⁄6
3⁄6 + 2⁄6 = 5⁄6
Mnożenie ułamków: Mnożymy licznik przez licznik i mianownik przez mianownik.
Przykład: 2⁄3 x 1⁄4 = 2 x 1⁄3 x 4 = 2⁄12 = 1⁄6 (po skróceniu)
Dzielenie ułamków: Mnożymy pierwszy ułamek przez odwrotność drugiego ułamka. Odwrotność ułamka to ułamek, w którym zamieniliśmy licznik z mianownikiem.
Przykład: 1⁄2 : 1⁄4 = 1⁄2 x 4⁄1 = 4⁄2 = 2
Praktyczne zastosowanie: Gdzie spotykamy liczby naturalne i ułamki?
Liczby naturalne i ułamki otaczają nas wszędzie!
- Gotowanie: Używamy ułamków do odmierzania składników, np. pół szklanki mąki (1⁄2 szklanki).
- Sport: Mierzymy czas w ułamkach sekund, np. 10,5 sekundy w biegu na 100 metrów.
- Zakupy: Obliczamy rabaty procentowe, np. 25% zniżki na koszulkę. (Procenty to tak naprawdę ułamki o mianowniku 100).
- Podróże: Określamy odległości na mapie w kilometrach (liczby naturalne) i częściach kilometra (ułamki).
- Dzielenie się: Dzielimy ciasto pomiędzy przyjaciół.
Wyobraź sobie, że pieczesz ciasto i przepis wymaga 1⁄4 szklanki cukru. Albo dzielisz pizzę na 8 kawałków i chcesz dać 1⁄2 pizzy swojemu bratu. Wtedy właśnie używasz ułamków!
Podsumowanie i dalsza przygoda z matematyką
W tym artykule poznaliśmy liczby naturalne, podstawowe działania na nich, oraz ułamki zwykłe – ich rodzaje, zamianę, rozszerzanie, skracanie, porównywanie oraz działania. Zobaczyliśmy, że matematyka nie jest tylko zbiorem wzorów, ale narzędziem, które pomaga nam zrozumieć świat i rozwiązywać codzienne problemy.
Ćwiczenia czynią mistrza! Im więcej zadań rozwiążecie, tym lepiej zrozumiecie liczby naturalne i ułamki. Nie bójcie się zadawać pytań i szukać odpowiedzi. Matematyka to fascynująca przygoda, a ten artykuł to dopiero początek Waszej podróży! Powodzenia! Pamiętajcie, matematyka jest wszędzie!