Liczby Naturalne I Ułamki Klasa 6

Witajcie, drodzy szóstoklasiści! Rozumiem, że matematyka czasem wydaje się trudna, a liczby naturalne i ułamki mogą sprawiać problemy. Pamiętajcie, że nie jesteście sami! Wielu uczniów mierzy się z podobnymi wyzwaniami. Ważne jest, by nie zniechęcać się i poszukiwać sposobów na zrozumienie tych zagadnień.

W tym artykule postaram się w przystępny sposób wyjaśnić, czym są liczby naturalne i ułamki, jak wykonywać na nich działania oraz jak wykorzystywać je w życiu codziennym. Skupimy się na praktycznych przykładach i prostych wyjaśnieniach, które pomogą Wam pokonać trudności.

Czym są liczby naturalne?

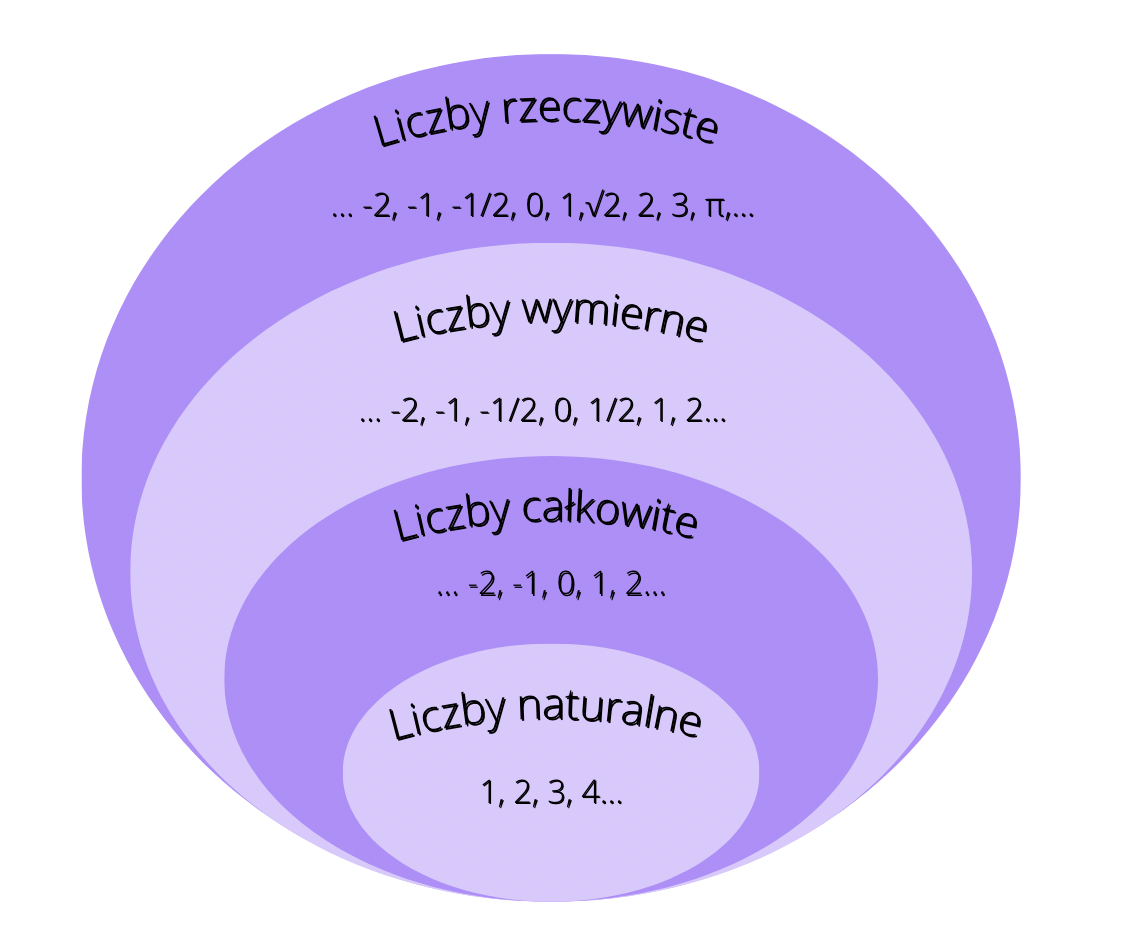
Liczby naturalne to najprostsze liczby, których używamy do liczenia. Wyobraźcie sobie, że macie koszyk jabłek. Możecie policzyć, ile ich jest: jedno jabłko, dwa jabłka, trzy jabłka... Te liczby, których używacie do liczenia przedmiotów, to właśnie liczby naturalne.

Formalnie, zbiór liczb naturalnych to: 0, 1, 2, 3, 4, 5, i tak dalej, aż do nieskończoności. Czasami zero nie jest zaliczane do liczb naturalnych. To zależy od definicji, której używamy. Najważniejsze, że każda liczba naturalna jest liczbą całkowitą (nie ma części ułamkowej) i jest nieujemna.

Przykłady liczb naturalnych:

Liczba uczniów w klasie.
Liczba stron w książce.
Liczba drzew w sadzie.

Działania na liczbach naturalnych

Możemy wykonywać różne działania na liczbach naturalnych: dodawanie, odejmowanie, mnożenie i dzielenie (czasem z resztą). Spróbujmy zrozumieć to na prostych przykładach:

Dodawanie: Jeśli masz 3 jabłka i dostaniesz jeszcze 2, to razem będziesz miał 3 + 2 = 5 jabłek.
Odejmowanie: Jeśli masz 7 cukierków i zjesz 3, to zostanie Ci 7 - 3 = 4 cukierki.
Mnożenie: Jeśli masz 4 paczki ciastek, a w każdej paczce są 3 ciastka, to razem masz 4 * 3 = 12 ciastek.
Dzielenie: Jeśli masz 10 batonów i chcesz je równo rozdzielić pomiędzy 5 przyjaciół, to każdy dostanie 10 / 5 = 2 batony. W niektórych przypadkach dzielenie nie jest idealne. Na przykład, jeśli masz 11 batonów i chcesz je podzielić pomiędzy 5 osób, to każdy dostanie 2 batony, a 1 baton zostanie (reszta z dzielenia).

Ułamki – co to takiego?

Ułamki reprezentują części całości. Wyobraźcie sobie pizzę pokrojoną na 8 równych kawałków. Jeśli zjesz 1 kawałek, to zjadłeś 1/8 pizzy. Ułamek składa się z licznika (liczba na górze) i mianownika (liczba na dole). Mianownik mówi nam, na ile części podzielono całość, a licznik mówi nam, ile tych części mamy.

Przykłady ułamków:

1/2 (jedna druga) – połowa
1/4 (jedna czwarta) – ćwierć
3/4 (trzy czwarte)
2/5 (dwie piąte)

Istnieją różne rodzaje ułamków:

Ułamki właściwe: Licznik jest mniejszy od mianownika (np. 2/5). Reprezentują one wartości mniejsze od 1.
Ułamki niewłaściwe: Licznik jest większy lub równy mianownikowi (np. 5/2). Reprezentują one wartości większe lub równe 1.
Liczby mieszane: Składają się z liczby naturalnej i ułamka właściwego (np. 2 1/2). Są to po prostu inny sposób zapisu ułamków niewłaściwych.

Działania na ułamkach

Działania na ułamkach mogą wydawać się skomplikowane, ale z odpowiednim podejściem stają się łatwiejsze. Ważne jest, aby zapamiętać kilka zasad:

Dodawanie i odejmowanie ułamków o tych samych mianownikach: Dodajemy lub odejmujemy liczniki, a mianownik pozostaje bez zmian. Na przykład: 2/7 + 3/7 = (2+3)/7 = 5/7. Podobnie: 5/8 - 2/8 = (5-2)/8 = 3/8.
Dodawanie i odejmowanie ułamków o różnych mianownikach: Musimy sprowadzić ułamki do wspólnego mianownika, czyli znaleźć liczbę, która jest podzielna przez oba mianowniki. Najczęściej używamy najmniejszej wspólnej wielokrotności (NWW) mianowników. Następnie rozszerzamy ułamki, aby miały ten sam mianownik. Na przykład: 1/2 + 1/3. NWW(2, 3) = 6. Zatem: 1/2 = 3/6 i 1/3 = 2/6. Stąd: 1/2 + 1/3 = 3/6 + 2/6 = 5/6.
Mnożenie ułamków: Mnożymy licznik przez licznik i mianownik przez mianownik. Na przykład: 1/2 * 2/3 = (1*2)/(2*3) = 2/6 = 1/3 (po skróceniu).
Dzielenie ułamków: Dzielenie ułamków to mnożenie przez odwrotność drugiego ułamka. Odwrotność ułamka to zamiana licznika z mianownikiem. Na przykład: 1/2 : 2/3 = 1/2 * 3/2 = (1*3)/(2*2) = 3/4.

Skracanie i rozszerzanie ułamków

Skracanie ułamków polega na podzieleniu licznika i mianownika przez tę samą liczbę, aż do uzyskania ułamka nieskracalnego (czyli takiego, którego licznika i mianownika nie da się już podzielić przez żadną wspólną liczbę inną niż 1). Na przykład: 4/8. Zarówno 4, jak i 8 są podzielne przez 4. Dzieląc licznik i mianownik przez 4, otrzymujemy: 4/8 = 1/2.

Rozszerzanie ułamków polega na pomnożeniu licznika i mianownika przez tę samą liczbę. Na przykład: 1/3. Chcemy rozszerzyć ten ułamek do ułamka o mianowniku 6. Musimy pomnożyć mianownik (3) przez 2, aby otrzymać 6. Zatem musimy również pomnożyć licznik (1) przez 2. Stąd: 1/3 = 2/6.

Liczby naturalne i ułamki w życiu codziennym

Liczby naturalne i ułamki są obecne w wielu aspektach naszego życia. Oto kilka przykładów:

Gotowanie: Przepisy często podają ilości składników w postaci ułamków (np. 1/2 szklanki mąki, 1/4 łyżeczki soli).
Zakupy: Promocje w sklepach często wyrażone są w procentach (np. 20% zniżki), które można przeliczyć na ułamki (20% = 20/100 = 1/5).
Mierzenie czasu: Godziny i minuty to części dnia, które można wyrazić za pomocą ułamków (np. 15 minut to 1/4 godziny).
Podróżowanie: Odległości między miastami i czas podróży można wyrazić za pomocą liczb naturalnych i ułamków (np. 250 km, 2 1/2 godziny).
Sport: Wyniki sportowe często wykorzystują ułamki do określenia pozycji zawodników.

Częste błędy i jak ich unikać

Podczas pracy z liczbami naturalnymi i ułamkami łatwo o pomyłki. Oto kilka najczęstszych błędów i wskazówki, jak ich unikać:

Zapominanie o sprowadzeniu ułamków do wspólnego mianownika przed dodawaniem lub odejmowaniem. Pamiętaj, że dodawać i odejmować możesz tylko ułamki o tym samym mianowniku.
Błędne skracanie ułamków. Upewnij się, że dzielisz zarówno licznik, jak i mianownik przez tę samą liczbę.
Pomylenie licznika z mianownikiem. Zawsze sprawdzaj, czy licznik jest na górze, a mianownik na dole.
Nieuważne czytanie treści zadania. Zanim zaczniesz rozwiązywać zadanie, dokładnie przeczytaj treść i upewnij się, że rozumiesz, o co pytają.

Jeśli popełniasz błędy, nie zniechęcaj się. Analizuj swoje błędy, staraj się zrozumieć, dlaczego je popełniłeś i ucz się na nich. Praktyka czyni mistrza! Im więcej ćwiczysz, tym lepiej będziesz radził sobie z liczbami naturalnymi i ułamkami.

Niektórzy twierdzą, że matematyka jest tylko zbiorem wzorów i reguł. Jednak matematyka to narzędzie, które pozwala nam zrozumieć i opisać świat wokół nas. Dzięki matematyce możemy rozwiązywać problemy, podejmować decyzje i rozwijać nasze umiejętności logicznego myślenia.

Mam nadzieję, że ten artykuł pomógł Wam lepiej zrozumieć liczby naturalne i ułamki. Pamiętajcie, że kluczem do sukcesu jest regularna nauka i praktyka. Nie bójcie się zadawać pytań i szukać pomocy, jeśli czegoś nie rozumiecie. Powodzenia!

Jakie są Wasze ulubione sposoby na naukę matematyki? Podzielcie się swoimi pomysłami!