Liczby Naturalne I Ułamki Kl 6

Hej! Jeśli jesteś w klasie 6 i masz wrażenie, że liczby naturalne i ułamki to czarna magia, nie martw się! Wielu uczniów w Twoim wieku czuje się podobnie. Zrozumienie tych zagadnień może wydawać się trudne, ale obiecuję, że krok po kroku wszystko stanie się jasne. Pamiętaj, że matematyka jest jak budowanie z klocków – każdy element jest ważny, a fundamenty muszą być solidne. Dlatego właśnie skupimy się na podstawach i postaramy się je porządnie utrwalić.

Po co mi to w ogóle? Liczby naturalne i ułamki w życiu codziennym.

Możesz pomyśleć: "Kiedy ja to wykorzystam?". Odpowiedź brzmi: bardzo często!

Zakupy: Obliczanie rabatów, sprawdzanie, czy wystarczy pieniędzy na wszystko, dzielenie kosztów z przyjaciółmi – to wszystko wymaga ułamków i liczb naturalnych. Wyobraź sobie, że kupujesz koszulkę przecenioną o 1/4. Musisz wiedzieć, ile zapłacisz, prawda?
Gotowanie: Przepisy często podają składniki w ułamkach. Musisz wiedzieć, ile mąki wsypać, żeby ciasto wyszło idealne.
Podróże: Obliczanie odległości na mapie, szacowanie czasu podróży, przeliczanie walut – liczby naturalne i ułamki są tu niezastąpione.
Sport: Sprawdzanie statystyk, porównywanie wyników, obliczanie średniej prędkości – bez liczb ani rusz!

Widzisz? Matematyka jest wszędzie! A liczby naturalne i ułamki to jej podstawowe narzędzia.

Liczby naturalne – fundamenty matematyki

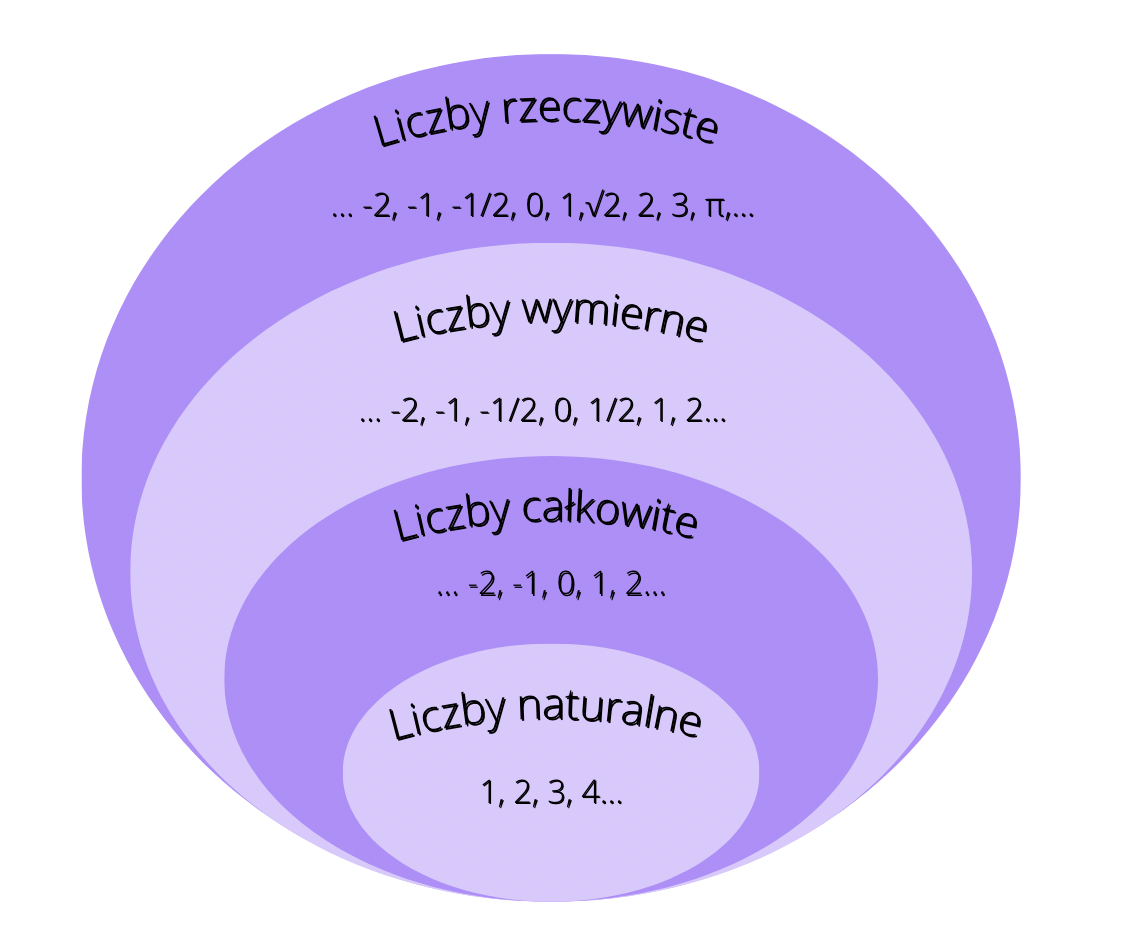
Liczby naturalne to po prostu liczby, których używamy do liczenia: 1, 2, 3, 4, 5, i tak dalej... Nie ma ułamków, nie ma liczb ujemnych, tylko całe, dodatnie liczby. Możemy z ich pomocą liczyć przedmioty, osoby, zwierzęta – wszystko, co da się policzyć w całości.

Działania na liczbach naturalnych

Podstawowe działania na liczbach naturalnych to:

Dodawanie: Łączenie dwóch lub więcej liczb, np. 2 + 3 = 5.
Odejmowanie: Odbieranie jednej liczby od drugiej, np. 5 - 2 = 3. Pamiętaj, że w zbiorze liczb naturalnych odejmowanie jest możliwe tylko wtedy, gdy odejmowana liczba jest mniejsza lub równa odjemnej.
Mnożenie: Skrócone dodawanie tej samej liczby, np. 3 x 4 = 4 + 4 + 4 = 12.
Dzielenie: Dzielenie jednej liczby na równe części, np. 12 : 3 = 4. Podobnie jak przy odejmowaniu, w zbiorze liczb naturalnych dzielenie nie zawsze jest możliwe (np. 5 : 2 nie daje wyniku będącego liczbą naturalną).

Ćwiczenie czyni mistrza! Im więcej będziesz ćwiczyć, tym lepiej zrozumiesz te działania.

Ułamki – kiedy całość to za mało

Ułamki pojawiają się, gdy potrzebujemy wyrazić część całości. Na przykład, jeśli podzielisz pizzę na 8 kawałków i zjesz 3 z nich, to zjadłeś 3/8 pizzy. Ułamek składa się z licznika (liczby nad kreską ułamkową) i mianownika (liczby pod kreską ułamkową). Mianownik mówi nam, na ile części podzielona jest całość, a licznik – ile tych części bierzemy.

Rodzaje ułamków

Ułamki zwykłe: Mają licznik i mianownik, np. 1/2, 3/4, 5/8.
Ułamki właściwe: Licznik jest mniejszy od mianownika, np. 2/3, 4/5, 7/9. Reprezentują one mniej niż jedną całość.
Ułamki niewłaściwe: Licznik jest większy lub równy mianownikowi, np. 5/3, 7/4, 9/9. Reprezentują one jedną całość lub więcej.
Liczby mieszane: Składają się z liczby naturalnej i ułamka właściwego, np. 1 1/2, 2 3/4, 3 1/5. Można je zamienić na ułamki niewłaściwe i odwrotnie.

Działania na ułamkach

Działania na ułamkach mogą wydawać się bardziej skomplikowane niż na liczbach naturalnych, ale spokojnie, dasz radę!

Dodawanie i odejmowanie ułamków o tych samych mianownikach: Dodajemy lub odejmujemy liczniki, a mianownik pozostaje bez zmian. Na przykład: 2/5 + 1/5 = 3/5.
Dodawanie i odejmowanie ułamków o różnych mianownikach: Musimy sprowadzić ułamki do wspólnego mianownika (najczęściej najmniejszej wspólnej wielokrotności mianowników). Na przykład: 1/2 + 1/3 = 3/6 + 2/6 = 5/6.
Mnożenie ułamków: Mnożymy licznik przez licznik i mianownik przez mianownik. Na przykład: 1/2 x 2/3 = 2/6.
Dzielenie ułamków: Mnożymy pierwszy ułamek przez odwrotność drugiego ułamka. Na przykład: 1/2 : 2/3 = 1/2 x 3/2 = 3/4.

Pamiętaj o skracaniu ułamków, aby otrzymać wynik w najprostszej postaci!

Porównywanie ułamków – który jest większy?

Porównywanie ułamków jest ważne, żeby wiedzieć, która część jest większa. Można to robić na kilka sposobów:

Ułamki o tych samych mianownikach: Większy jest ten, który ma większy licznik. Na przykład: 3/5 > 2/5.
Ułamki o tych samych licznikach: Większy jest ten, który ma mniejszy mianownik. Na przykład: 1/2 > 1/3.
Ułamki o różnych licznikach i mianownikach: Sprowadzamy ułamki do wspólnego mianownika i porównujemy liczniki. Na przykład: 2/3 i 3/4. Sprowadzamy do mianownika 12: 8/12 i 9/12. Więc 3/4 > 2/3.

Można też porównywać ułamki, zamieniając je na liczby dziesiętne (o tym za chwilę!).

Ułamki dziesiętne – inna forma zapisu

Ułamki dziesiętne to ułamki, które mają w mianowniku 10, 100, 1000, itd. Można je zapisać za pomocą przecinka, np. 0,5 (czyli 5/10), 0,25 (czyli 25/100), 0,75 (czyli 75/100). Ułamki dziesiętne ułatwiają porównywanie i wykonywanie działań.

Zamiana ułamków zwykłych na dziesiętne i odwrotnie

Ułamek zwykły na dziesiętny: Dzielimy licznik przez mianownik. Na przykład: 1/2 = 0,5, 3/4 = 0,75. Czasami trzeba podzielić pisemnie.
Ułamek dziesiętny na zwykły: Zapisujemy ułamek dziesiętny jako ułamek zwykły z mianownikiem 10, 100, 1000, itd., a następnie skracamy go, jeśli to możliwe. Na przykład: 0,5 = 5/10 = 1/2, 0,25 = 25/100 = 1/4.

Niektóre ułamki zwykłe mają rozwinięcia dziesiętne nieskończone (np. 1/3 = 0,333...). W takich przypadkach możemy zaokrąglić ułamek dziesiętny do odpowiedniej liczby miejsc po przecinku.

Pułapki i błędy – na co uważać?

Nawet najlepsi matematycy czasami popełniają błędy. Oto kilka pułapek, na które warto uważać:

Zapominanie o wspólnym mianowniku przy dodawaniu i odejmowaniu ułamków.
Mylenie kolejności działań. Pamiętaj o kolejności: nawiasy, mnożenie/dzielenie, dodawanie/odejmowanie.
Nieprawidłowe skracanie ułamków. Upewnij się, że dzielisz licznik i mianownik przez ten sam dzielnik.
Nieuważne czytanie treści zadań. Zawsze przeczytaj zadanie kilka razy, żeby zrozumieć, o co pytają.

Jeśli popełnisz błąd, nie zrażaj się! Przeanalizuj go, żeby zrozumieć, gdzie popełniłeś błąd, i spróbuj jeszcze raz.

Jak ćwiczyć? Metody i pomysły.

Najlepszy sposób na opanowanie liczb naturalnych i ułamków to ćwiczenia. Oto kilka pomysłów:

Rozwiązuj zadania z podręcznika i zeszytu ćwiczeń.
Korzystaj z darmowych zasobów internetowych. Jest mnóstwo stron i aplikacji z ćwiczeniami z matematyki.
Grają w gry matematyczne. To świetny sposób na naukę przez zabawę.
Rozwiązuj zadania z życia codziennego. Na przykład, oblicz, ile zapłacisz za zakupy, albo podziel ciasto na równe kawałki dla swoich przyjaciół.
Poproś o pomoc nauczyciela, rodziców lub starszego kolegę. Nie wstydź się pytać, jeśli czegoś nie rozumiesz.

Podsumowanie i kolejne kroki

Gratulacje! Dotarłeś do końca artykułu! Mam nadzieję, że teraz liczby naturalne i ułamki wydają się mniej straszne. Pamiętaj, że kluczem do sukcesu jest regularna praktyka i cierpliwość. Nie zrażaj się trudnościami, a z czasem wszystko stanie się jasne.

Teraz, gdy znasz już podstawy, możesz przejść do bardziej zaawansowanych zagadnień, takich jak procenty, proporcje czy równania. Świat matematyki stoi przed Tobą otworem!

Czy masz jakieś pytania, które chciałbyś zadać, albo zagadnienia, które chciałbyś, żebym wytłumaczył bardziej szczegółowo? Nie krępuj się!