Liczby I Działania Klasa 8 Gwo

Czy kiedykolwiek zdarzyło Ci się, że siedząc nad zadaniem z matematyki w ósmej klasie, czułeś się jakbyś próbował rozszyfrować obcy język? Liczby i działania – temat, który dla wielu uczniów staje się prawdziwym wyzwaniem. Nie martw się, nie jesteś sam! Matematyka w ósmej klasie to poważny krok w przód, ale z odpowiednim podejściem i zrozumieniem, możesz bez problemu opanować te zagadnienia.

Liczby Rzeczywiste: Podstawa Twojego Matematycznego Świata

Zacznijmy od podstaw – liczb rzeczywistych. To wszystkie liczby, które możesz znaleźć na osi liczbowej. Obejmują one liczby naturalne, całkowite, wymierne i niewymierne. Zrozumienie, które liczby należą do której kategorii, jest kluczowe do wykonywania operacji i rozwiązywania zadań.

Liczby Naturalne, Całkowite i Wymierne – Od czego Zaczynamy?

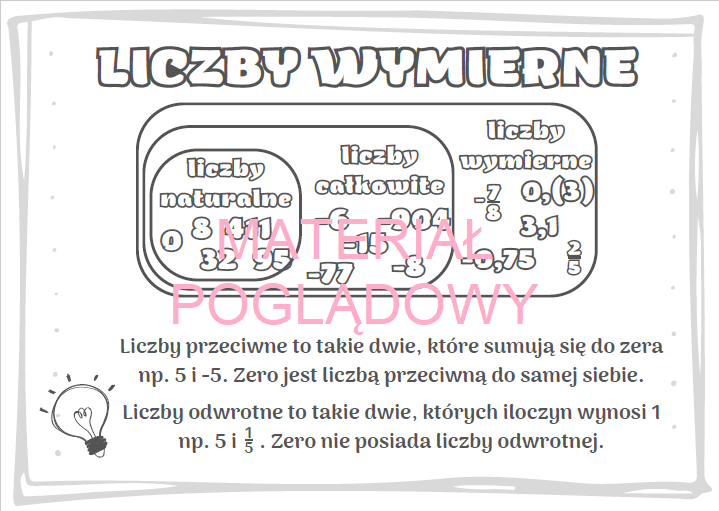
Liczby naturalne (1, 2, 3, …) to te, których używamy do liczenia przedmiotów. Liczby całkowite obejmują liczby naturalne, zero i liczby ujemne (-3, -2, -1, 0, 1, 2, 3, …). Liczby wymierne można zapisać w postaci ułamka a/b, gdzie a i b są liczbami całkowitymi, a b nie jest równe zero. Pamiętaj, że każda liczba całkowita jest również liczbą wymierną (np. 5 można zapisać jako 5/1).

Liczby Niewymierne: Co To Takiego?

To tutaj zaczyna się robić nieco bardziej skomplikowanie. Liczby niewymierne to liczby, których nie można zapisać w postaci ułamka. Przykładem jest √2 (pierwiastek kwadratowy z 2) lub liczba π (pi). Ich rozwinięcie dziesiętne jest nieskończone i nieokresowe, co oznacza, że cyfry po przecinku nie powtarzają się w regularnym wzorze. Zrozumienie, że liczby niewymierne istnieją i są częścią liczb rzeczywistych, jest bardzo ważne.

Działania na Liczbach Rzeczywistych: Klucz do Sukcesu

Teraz przejdźmy do działań. Dodawanie, odejmowanie, mnożenie i dzielenie – to podstawowe operacje, które musisz opanować. Ale w ósmej klasie dochodzą do tego potęgi i pierwiastki. Pamiętaj o kolejności wykonywania działań (nawiasy, potęgi/pierwiastki, mnożenie/dzielenie, dodawanie/odejmowanie – PEMDAS/BODMAS). To zasada, która pomoże Ci uniknąć błędów.

Potęgi i Pierwiastki: Wzory i Własności

Potęgi to skrócony sposób zapisywania wielokrotnego mnożenia tej samej liczby (np. 2³ = 2 * 2 * 2 = 8). Pierwiastki są operacją odwrotną do potęgowania (np. √9 = 3, bo 3² = 9). Zapamiętaj wzory na potęgowanie i pierwiastkowanie iloczynu, ilorazu i potęgi potęgi. Na przykład:

• (a * b)ⁿ = aⁿ * bⁿ
• (a / b)ⁿ = aⁿ / bⁿ
• (a^m)ⁿ = a^m*n

Znajomość tych wzorów ułatwi Ci rozwiązywanie bardziej skomplikowanych zadań.

Notacja Wykładnicza: Jak Zapisywać Bardzo Duże i Bardzo Małe Liczby?

Notacja wykładnicza (naukowa) to sposób zapisywania bardzo dużych lub bardzo małych liczb za pomocą potęgi liczby 10. Liczbę zapisujemy w postaci a * 10ⁿ, gdzie 1 ≤ |a| < 10, a n jest liczbą całkowitą. Na przykład, 3 000 000 zapisujemy jako 3 * 10⁶, a 0,00005 zapisujemy jako 5 * 10^-5. Notacja wykładnicza jest niezwykle przydatna w fizyce, chemii i innych naukach.

Procenty: Codzienna Matematyka

Procenty są wszędzie! W sklepach, w bankach, w statystykach. Musisz umieć obliczać procent z danej liczby, obliczać, o ile procent wzrosła lub zmalała jakaś wartość, oraz rozwiązywać zadania związane z lokatami i kredytami. Pamiętaj, że procent to ułamek o mianowniku 100 (np. 25% = 25/100 = 0,25).

Jak Obliczać Procent z Liczby?

Aby obliczyć x% z liczby y, wystarczy pomnożyć y przez x/100. Na przykład, aby obliczyć 20% z liczby 80, robimy: 80 * (20/100) = 80 * 0,2 = 16.

Zmiana Procentowa: Wzrost i Spadek

Aby obliczyć zmianę procentową, używamy wzoru: [(wartość końcowa - wartość początkowa) / wartość początkowa] * 100%. Jeśli wynik jest dodatni, to mamy do czynienia ze wzrostem. Jeśli wynik jest ujemny, to mamy do czynienia ze spadkiem. Na przykład, jeśli cena produktu wzrosła z 50 zł do 60 zł, to zmiana procentowa wynosi: [(60 - 50) / 50] * 100% = (10 / 50) * 100% = 20%. Czyli cena wzrosła o 20%.

Praktyczne Wskazówki i Przykłady

Ćwiczenie czyni mistrza! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz dany temat. Nie bój się prosić o pomoc nauczyciela lub kolegów z klasy. Wykorzystuj dostępne zasoby online, takie jak filmy instruktażowe i interaktywne ćwiczenia. Szukaj przykładów z życia codziennego, które pomogą Ci zrozumieć, jak matematyka działa w praktyce.

Przykłady Zastosowań w Życiu Codziennym

• Gotowanie: Obliczanie proporcji składników, przeliczanie jednostek (np. z gramów na mililitry).
• Zakupy: Obliczanie rabatów, sprawdzanie, czy promocja jest rzeczywiście opłacalna.
• Planowanie podróży: Obliczanie kosztów paliwa, szacowanie czasu podróży.
• Inwestycje: Obliczanie oprocentowania lokat, analiza ryzyka inwestycyjnego.

Podsumowanie: Matematyka Jest dla Ciebie!

Matematyka w ósmej klasie może wydawać się trudna, ale z odpowiednim podejściem i systematyczną pracą, możesz ją opanować. Pamiętaj o podstawach, ćwicz regularnie, szukaj pomocy, gdy jej potrzebujesz, i nie bój się popełniać błędów. Błędy są częścią procesu uczenia się. Kluczem jest zrozumienie, dlaczego popełniłeś błąd, i wyciągnięcie z niego wniosków. Zaufaj sobie, a przekonasz się, że liczby i działania nie są takie straszne, jak się wydają!

Powodzenia! Pamiętaj, matematyka to nie kara, to narzędzie! Użyj go mądrze, a otworzy przed Tobą wiele drzwi.