Liczby I Działania Klasa 7

Czy kiedykolwiek zastanawiałeś się, jak matematyka wpływa na twoje codzienne życie? Od planowania kieszonkowego po obliczanie czasu potrzebnego na dojazd do szkoły, liczby i działania odgrywają kluczową rolę. Ten artykuł, skierowany do uczniów klasy 7, ma na celu pomóc w zrozumieniu i opanowaniu podstawowych koncepcji związanych z liczbami i działaniami, co pozwoli wam pewniej poruszać się w świecie matematyki.

Rodzaje Liczb

Na początek, przyjrzyjmy się różnym rodzajom liczb, z którymi spotkamy się w klasie 7 i później.

Liczby Naturalne (N)

Liczby naturalne to najprostszy rodzaj liczb. Używamy ich do liczenia przedmiotów. Zaczynają się od 1 i idą w górę: 1, 2, 3, 4, ... Ważne jest, że zero nie jest liczbą naturalną.

Liczby Całkowite (C)

Liczby całkowite to liczby naturalne, zero i liczby ujemne: ..., -3, -2, -1, 0, 1, 2, 3, ... Wyobraź sobie termometr – wartości powyżej zera to liczby naturalne, zero to punkt odniesienia, a wartości poniżej zera to liczby ujemne. Liczby całkowite pozwalają nam opisywać zarówno zyski, jak i straty.

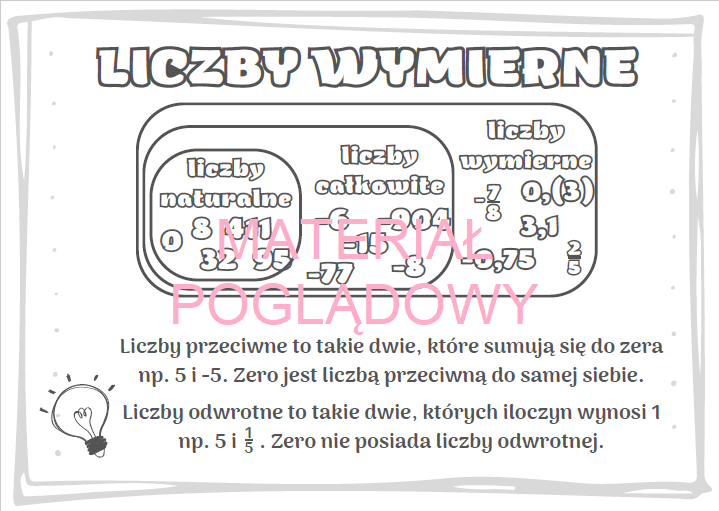
Liczby Wymierne (W)

Liczby wymierne to wszystkie liczby, które można zapisać w postaci ułamka zwykłego a/b, gdzie a jest liczbą całkowitą, a b jest liczbą całkowitą różną od zera. Przykłady to: 1/2, -3/4, 5, -7. Ważne jest, że każda liczba całkowita jest również liczbą wymierną (np. 5 można zapisać jako 5/1). Liczby wymierne to również rozwinięcia dziesiętne skończone (np. 0,25) i rozwinięcia dziesiętne nieskończone okresowe (np. 0,(3) = 0,333...).

Przykład: Pomyśl o pizzy. Możesz zjeść całą pizzę (liczba 1), pół pizzy (1/2), albo trzy kawałki z ośmiu (3/8). Wszystkie te ilości można wyrazić za pomocą liczb wymiernych.

Liczby Niewymierne

Liczby niewymierne to liczby, których nie da się zapisać w postaci ułamka zwykłego. Ich rozwinięcia dziesiętne są nieskończone i nieokresowe. Najbardziej znanym przykładem jest liczba Pi (π ≈ 3,14159...), która pojawia się przy obliczaniu obwodu i pola koła. Inne przykłady to pierwiastki kwadratowe z liczb, które nie są kwadratami liczb całkowitych, np. √2, √3, √5.

Liczby Rzeczywiste (R)

Liczby rzeczywiste to wszystkie liczby wymierne i niewymierne razem. Innymi słowy, każda liczba, którą możemy umieścić na osi liczbowej, jest liczbą rzeczywistą.

Działania na Liczbach

Znamy już różne rodzaje liczb, więc teraz przyjrzyjmy się działaniom, które możemy na nich wykonywać.

Dodawanie i Odejmowanie

Dodawanie to łączenie dwóch lub więcej liczb w jedną sumę. Odejmowanie to znajdowanie różnicy między dwiema liczbami.

Dodawanie liczb o tych samych znakach: Dodajemy wartości bezwzględne liczb i dopisujemy wspólny znak. Np. (-3) + (-5) = -8.
Dodawanie liczb o różnych znakach: Odejmujemy od większej wartości bezwzględnej mniejszą wartość bezwzględną i dopisujemy znak liczby o większej wartości bezwzględnej. Np. (-7) + 4 = -3.
Odejmowanie: Odejmowanie to dodawanie liczby przeciwnej. Np. 5 - 3 = 5 + (-3) = 2.

Przykład: Wyobraź sobie, że masz 5 zł, a potem dostajesz od babci 3 zł. Masz teraz 8 zł (5 + 3 = 8). Jeśli natomiast wydasz 2 zł, to zostanie ci 6 zł (8 - 2 = 6).

Mnożenie i Dzielenie

Mnożenie to powtarzane dodawanie tej samej liczby. Dzielenie to dzielenie liczby na równe części.

Mnożenie i dzielenie liczb o tych samych znakach: Wynik jest dodatni. Np. (-2) * (-3) = 6, 8 / 2 = 4.
Mnożenie i dzielenie liczb o różnych znakach: Wynik jest ujemny. Np. (-4) * 3 = -12, 10 / (-2) = -5.
Pamiętaj o kolejności wykonywania działań: Najpierw nawiasy, potem potęgowanie i pierwiastkowanie, następnie mnożenie i dzielenie, a na końcu dodawanie i odejmowanie.

Przykład: Masz 3 paczki ciastek, a w każdej paczce są 4 ciastka. Razem masz 12 ciastek (3 * 4 = 12). Jeśli chcesz podzielić te ciastka równo między 6 osób, każda osoba dostanie 2 ciastka (12 / 6 = 2).

Potęgowanie i Pierwiastkowanie

Potęgowanie to mnożenie liczby przez samą siebie określoną liczbę razy. Pierwiastkowanie to znajdowanie liczby, która pomnożona przez samą siebie (odpowiednią liczbę razy) daje daną liczbę.

Potęga o wykładniku naturalnym: aⁿ = a * a * ... * a (n razy). Np. 2³ = 2 * 2 * 2 = 8.
Potęga o wykładniku 0: a⁰ = 1 (dla a ≠ 0). Np. 5⁰ = 1.
Potęga o wykładniku ujemnym: a^-n = 1 / aⁿ. Np. 2^-2 = 1 / 2² = 1/4.
Pierwiastek kwadratowy: √a to liczba, która pomnożona przez samą siebie daje a. Np. √9 = 3, ponieważ 3 * 3 = 9.

Przykład: Chcesz obliczyć pole kwadratu o boku długości 5 cm. Pole kwadratu to bok razy bok, czyli 5² = 25 cm².

Działania na Ułamkach Zwykłych i Dziesiętnych

Ułamki, zarówno zwykłe jak i dziesiętne, są ważną częścią matematyki. Musimy umieć na nich wykonywać różne działania.

Ułamki Zwykłe

Ułamek zwykły to liczba postaci a/b, gdzie a to licznik, a b to mianownik.

Dodawanie i odejmowanie ułamków o tych samych mianownikach: Dodajemy lub odejmujemy liczniki, a mianownik pozostaje bez zmian. Np. 2/5 + 1/5 = 3/5.
Dodawanie i odejmowanie ułamków o różnych mianownikach: Sprowadzamy ułamki do wspólnego mianownika, a następnie dodajemy lub odejmujemy liczniki. Np. 1/2 + 1/3 = 3/6 + 2/6 = 5/6.
Mnożenie ułamków: Mnożymy licznik przez licznik i mianownik przez mianownik. Np. 2/3 * 1/4 = 2/12 = 1/6.
Dzielenie ułamków: Mnożymy pierwszy ułamek przez odwrotność drugiego ułamka. Np. 1/2 : 1/3 = 1/2 * 3/1 = 3/2.

Ułamki Dziesiętne

Ułamek dziesiętny to liczba zapisana z użyciem przecinka dziesiętnego. Np. 0,75, 3,14.

Dodawanie i odejmowanie ułamków dziesiętnych: Zapisujemy ułamki tak, aby przecinki były jeden pod drugim, a następnie dodajemy lub odejmujemy jak liczby całkowite.
Mnożenie ułamków dziesiętnych: Mnożymy ułamki jak liczby całkowite, a następnie przesuwamy przecinek w wyniku o tyle miejsc w lewo, ile łącznie miejsc po przecinku mają mnożone liczby.
Dzielenie ułamków dziesiętnych: Przesuwamy przecinek w dzielnej i dzielniku o tyle miejsc w prawo, aby dzielnik był liczbą całkowitą, a następnie dzielimy jak liczby całkowite.

Przykład: Wyobraź sobie, że masz 0,5 kg mąki, a potrzebujesz 0,75 kg. Musisz dokupić 0,25 kg (0,75 - 0,5 = 0,25).

Procenty

Procent to sposób wyrażania liczby jako ułamka o mianowniku 100. Oznacza się go symbolem %. Na przykład, 25% to 25/100 = 0,25.

Obliczanie procentu z liczby: Mnożymy liczbę przez procent wyrażony jako ułamek dziesiętny. Np. 20% z 50 to 0,20 * 50 = 10.
Obliczanie liczby, gdy znamy jej procent: Dzielimy znaną wartość przez procent wyrażony jako ułamek dziesiętny. Np. Jeśli 10 to 20% szukanej liczby, to szukana liczba to 10 / 0,20 = 50.
Obliczanie jakim procentem jednej liczby jest druga liczba: Dzielimy jedną liczbę przez drugą i mnożymy wynik przez 100%. Np. Jakim procentem liczby 50 jest liczba 10? (10 / 50) * 100% = 20%.

Przykład: Kupujesz buty, które kosztują 100 zł, a sklep oferuje rabat 15%. Oszczędzasz 15 zł (15% ze 100 = 0,15 * 100 = 15), więc zapłacisz 85 zł (100 - 15 = 85).

Wyrażenia Algebraiczne

Wyrażenie algebraiczne to wyrażenie, które zawiera liczby, litery (reprezentujące zmienne) i symbole działań.

Przykłady: 2x + 3, a - 5, 4y² - 1.
Upraszczanie wyrażeń algebraicznych: Łączymy wyrazy podobne (czyli wyrazy zawierające te same zmienne w tych samych potęgach). Np. 3x + 2x - y + 4y = 5x + 3y.
Wartość wyrażenia algebraicznego: Podstawiamy za zmienne konkretne liczby i obliczamy wartość wyrażenia. Np. Jeśli x = 2, to wartość wyrażenia 2x + 3 wynosi 2 * 2 + 3 = 7.

Przykład: Wyobraź sobie, że masz x jabłek i twój kolega ma o 3 jabłka więcej. Razem macie x + (x + 3) = 2x + 3 jabłek.

Podsumowanie

Opanowanie liczb i działań to fundament do zrozumienia bardziej zaawansowanych zagadnień matematycznych. Pamiętajcie, że praktyka czyni mistrza! Im więcej ćwiczycie, tym lepiej zrozumiecie te koncepcje i tym pewniej będziecie się czuli rozwiązując zadania. Nie bójcie się zadawać pytań i szukać pomocy, gdy macie problemy. Matematyka może być fascynująca i użyteczna, jeśli podejdziecie do niej z ciekawością i determinacją. Mamy nadzieję, że ten artykuł pomógł wam uporządkować wiedzę i zmotywował do dalszej nauki. Powodzenia w waszej matematycznej podróży! Pamiętajcie, że zrozumienie tych podstaw pozwoli Wam na przykład na lepsze planowanie budżetu, obliczanie promocji w sklepach oraz rozwiązywanie problemów w życiu codziennym.