Liczby I Działania Klasa 5

Hej uczniowie klasy 5! Czy liczby i działania wydają się Wam czasem zagadką? Nie martwcie się! Ten artykuł powstał specjalnie dla Was, aby w przystępny sposób wyjaśnić podstawowe zagadnienia związane z liczbami i działaniami, które są tak ważne w matematyce. Razem odkryjemy, że matematyka może być fascynująca i zrozumiała!

Co znajdziesz w tym artykule?

Przygotowaliśmy dla Was kompleksowy przewodnik po świecie liczb i działań, obejmujący:

Rodzaje liczb: Naturalne, całkowite, ułamki zwykłe i dziesiętne.
Działania arytmetyczne: Dodawanie, odejmowanie, mnożenie i dzielenie - przypomnimy sobie zasady i triki!
Kolejność wykonywania działań: Dlaczego jest tak ważna i jak o niej pamiętać?
Własności działań: Prawo przemienności, łączności i rozdzielności – jak je wykorzystywać?
Dzielniki i wielokrotności: Co to takiego i jak je znajdować?
Liczby pierwsze i złożone: Fascynujący świat liczb, które dzielą się tylko przez 1 i samą siebie!
Zaokrąglanie liczb: Kiedy i jak zaokrąglamy liczby?
Proste zadania tekstowe: Jak krok po kroku rozwiązywać zadania z życia wzięte?

Pamiętajcie, że matematyka to nie tylko wzory i reguły, ale przede wszystkim logiczne myślenie i umiejętność rozwiązywania problemów. Zapraszamy do wspólnej podróży po świecie liczb!

Rodzaje liczb – poznajmy się!

Zacznijmy od podstaw – od samych liczb. Spotykamy je wszędzie, ale czy wiemy, jakie są ich rodzaje?

Liczby naturalne

Liczby naturalne to te, których używamy do liczenia: 1, 2, 3, 4, 5 i tak dalej... Zaczynają się od 1 i biegną w nieskończoność. Używamy ich, gdy chcemy policzyć, ile mamy jabłek, ile osób jest w klasie, albo ile stron ma książka. Zauważcie, że 0 nie jest liczbą naturalną.

Przykład: Masz 3 kredki. Liczba 3 jest liczbą naturalną.

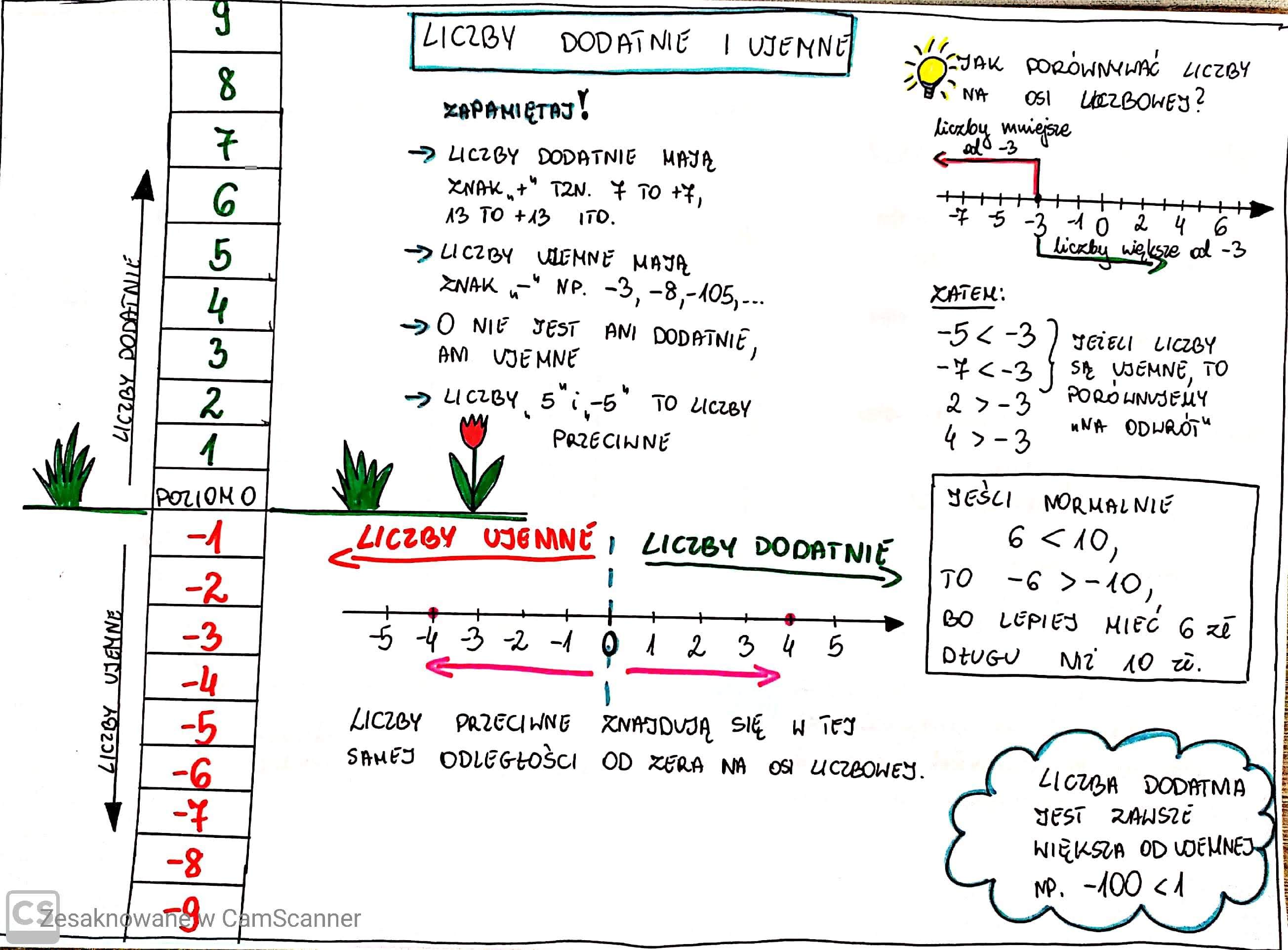
Liczby całkowite

Liczby całkowite to liczby naturalne, zero (0) oraz liczby ujemne: ..., -3, -2, -1, 0, 1, 2, 3, ... Dodajemy do liczb naturalnych "minusy". Ujemne liczby często opisują długi (np. masz dług -5 zł) lub temperaturę (np. -2 stopnie Celsjusza).

Przykład: Temperatura na dworze wynosi -5 stopni Celsjusza. Liczba -5 jest liczbą całkowitą.

Ułamki zwykłe

Ułamki zwykłe to liczby zapisane w postaci licznika i mianownika, np. 1/2, 3/4, 7/8. Licznik (górna liczba) pokazuje, ile części bierzemy z całości, a mianownik (dolna liczba) pokazuje, na ile części podzieliliśmy całość. Pomyślcie o pizzy! Jeśli podzielicie ją na 4 kawałki i zjecie 1, to zjedliście 1/4 pizzy.

Przykład: Zjadłeś 2 kawałki tortu podzielonego na 8 części. Zjadłeś 2/8 tortu.

Ułamki dziesiętne

Ułamki dziesiętne to liczby, w których używamy przecinka, np. 0,5, 1,75, 3,14. To inny sposób zapisu ułamków zwykłych, gdzie mianownik jest potęgą liczby 10 (10, 100, 1000...). Ułamki dziesiętne są bardzo wygodne do wykonywania obliczeń, szczególnie przy użyciu kalkulatora.

Przykład: Książka kosztuje 12,50 zł. Liczba 12,50 jest ułamkiem dziesiętnym.

Działania arytmetyczne – cztery podstawowe kroki

Teraz przejdźmy do tego, co możemy robić z liczbami, czyli do działań arytmetycznych. Mamy cztery podstawowe działania:

Dodawanie (+): Łączenie liczb w jedną całość. Przykład: 2 + 3 = 5
Odejmowanie (-): Zabieranie jednej liczby od drugiej. Przykład: 5 - 2 = 3
Mnożenie (* lub ·): Dodawanie tej samej liczby wiele razy. Przykład: 3 * 4 = 12 (czyli 3 + 3 + 3 + 3 = 12)
Dzielenie (: lub /): Rozdzielanie liczby na równe części. Przykład: 12 / 3 = 4 (czyli 12 podzielone na 3 równe części daje 4)

Pamiętajcie, żeby dobrze opanować te działania. To podstawa do dalszej nauki matematyki!

Kolejność wykonywania działań – dyktator matematyki!

Kolejność wykonywania działań jest bardzo ważna. Jeśli nie będziemy jej przestrzegać, to możemy otrzymać błędny wynik. Pamiętajcie o regule PEMDAS/BODMAS (w zależności od kraju):

P/B - Nawiasy (Parentheses/Brackets) - Wykonujemy działania w nawiasach, zaczynając od najbardziej wewnętrznych.
E/O - Potęgi/Pierwiastki (Exponents/Orders) - Wykonujemy potęgowanie i pierwiastkowanie (w klasie 5 zwykle tego nie mamy).
M/D - Mnożenie i Dzielenie (Multiplication and Division) - Wykonujemy mnożenie i dzielenie, od lewej do prawej.
A/S - Dodawanie i Odejmowanie (Addition and Subtraction) - Wykonujemy dodawanie i odejmowanie, od lewej do prawej.

Przykład: 2 + 3 * 4 = ? Najpierw mnożymy 3 * 4 = 12, a potem dodajemy 2. Więc 2 + 12 = 14. Gdybyśmy najpierw dodali, wyszłoby 5 * 4 = 20, co jest źle!

Własności działań – matematyczne skróty

Działania mają pewne własności, które mogą ułatwić nam obliczenia:

Prawo przemienności: Zmieniając kolejność składników w dodawaniu lub czynników w mnożeniu, wynik się nie zmieni. Czyli:
- a + b = b + a (np. 2 + 3 = 3 + 2)
- a * b = b * a (np. 2 * 3 = 3 * 2)
Prawo łączności: Kolejność wykonywania dodawania lub mnożenia kilku liczb nie wpływa na wynik (jeśli nie ma nawiasów). Czyli:
- (a + b) + c = a + (b + c) (np. (2 + 3) + 4 = 2 + (3 + 4))
- (a * b) * c = a * (b * c) (np. (2 * 3) * 4 = 2 * (3 * 4))
Prawo rozdzielności mnożenia względem dodawania: Mnożenie liczby przez sumę jest równe sumie iloczynów tej liczby przez każdy składnik sumy. Czyli: a * (b + c) = a * b + a * c (np. 2 * (3 + 4) = 2 * 3 + 2 * 4)

Wykorzystywanie tych własności może znacznie uprościć obliczenia, szczególnie w pamięci!

Dzielniki i wielokrotności – matematyczne rodziny

Dzielniki i wielokrotności to pojęcia, które pomagają nam zrozumieć relacje między liczbami.

Dzielnik

Dzielnik liczby to liczba, przez którą dana liczba dzieli się bez reszty. Na przykład, dzielnikami liczby 12 są: 1, 2, 3, 4, 6 i 12.

Wielokrotność

Wielokrotność liczby to liczba, która powstaje przez pomnożenie danej liczby przez liczbę naturalną. Na przykład, wielokrotnościami liczby 3 są: 3, 6, 9, 12, 15 i tak dalej.

Znajomość dzielników i wielokrotności przydaje się np. przy skracaniu ułamków.

Liczby pierwsze i złożone – wyjątkowe i "towarzyskie"

Liczby możemy podzielić na dwie grupy: liczby pierwsze i liczby złożone.

Liczby pierwsze

Liczba pierwsza to liczba naturalna większa od 1, która ma tylko dwa dzielniki: 1 i samą siebie. Przykłady liczb pierwszych: 2, 3, 5, 7, 11, 13, 17, 19, ... Liczba 2 jest jedyną parzystą liczbą pierwszą!

Liczby złożone

Liczba złożona to liczba naturalna większa od 1, która ma więcej niż dwa dzielniki. Przykłady liczb złożonych: 4, 6, 8, 9, 10, 12, 14, 15, ...

Każda liczba naturalna większa od 1 jest albo liczbą pierwszą, albo liczbą złożoną.

Zaokrąglanie liczb – przybliżenia w praktyce

Zaokrąglanie liczb to proces zastępowania liczby inną, przybliżoną wartością. Robimy to, gdy dokładna wartość nie jest nam potrzebna, albo gdy chcemy uprościć obliczenia. Zasady zaokrąglania:

Jeśli cyfra, która stoi za cyfrą, do której zaokrąglamy, jest mniejsza niż 5 (0, 1, 2, 3, 4), to cyfrę, do której zaokrąglamy, zostawiamy bez zmian, a wszystkie cyfry po niej zamieniamy na zera.
Jeśli cyfra, która stoi za cyfrą, do której zaokrąglamy, jest większa lub równa 5 (5, 6, 7, 8, 9), to cyfrę, do której zaokrąglamy, zwiększamy o 1, a wszystkie cyfry po niej zamieniamy na zera.

Przykłady:

Zaokrąglanie do pełnych dziesiątek: 23 ≈ 20, 27 ≈ 30
Zaokrąglanie do pełnych setek: 145 ≈ 100, 162 ≈ 200
Zaokrąglanie ułamków dziesiętnych do części dziesiątych: 3,14 ≈ 3,1, 3,16 ≈ 3,2

Proste zadania tekstowe – matematyka w życiu codziennym

Najważniejsze jest, aby nauczyć się wykorzystywać matematykę w praktyce. Rozwiązywanie zadań tekstowych to świetny sposób na to!

Oto kilka wskazówek:

Przeczytaj uważnie zadanie: Zrozum, o co pytają.
Wypisz dane: Zanotuj wszystkie liczby i informacje z zadania.
Ustal, jakie działanie trzeba wykonać: Czy trzeba dodać, odjąć, pomnożyć, czy podzielić? Czasami trzeba wykonać kilka działań.
Wykonaj obliczenia: Pamiętaj o kolejności wykonywania działań!
Sprawdź, czy wynik ma sens: Czy odpowiedź jest logiczna w kontekście zadania?
Napisz odpowiedź: Odpowiedz na pytanie z zadania pełnym zdaniem.

Przykład:

Zadanie: Ania kupiła 3 batony po 2 złote każdy i 2 lody po 3 złote każdy. Ile zapłaciła za wszystko?

Dane: 3 batony po 2 zł, 2 lody po 3 zł.
Działania: Mnożenie i dodawanie.
Obliczenia: 3 * 2 = 6 zł (batony), 2 * 3 = 6 zł (lody), 6 + 6 = 12 zł (razem).
Odpowiedź: Ania zapłaciła za wszystko 12 złotych.

Pamiętajcie, że ćwiczenie czyni mistrza! Im więcej zadań rozwiążecie, tym lepiej będziecie radzić sobie z matematyką.

Podsumowanie i co dalej?

Gratulacje! Dotarliście do końca tego artykułu. Mamy nadzieję, że pomógł Wam on zrozumieć podstawy liczb i działań. Pamiętajcie, że matematyka to proces, który wymaga czasu i ćwiczeń. Nie zrażajcie się trudnościami, pytajcie nauczycieli i kolegów, a przede wszystkim - bądźcie ciekawi!

Co możecie robić dalej?

Rozwiązujcie zadania z podręcznika.
Szukajcie dodatkowych materiałów w internecie (strony z ćwiczeniami, filmy edukacyjne).
Grajcie w gry matematyczne.
Wykorzystujcie matematykę w codziennych sytuacjach (np. obliczanie reszty w sklepie, mierzenie długości pokoju).

Pamiętajcie, że matematyka jest wszędzie! Powodzenia!