Liczby Dodatnie I Ujemne Klasa 7

Cześć, siódmoklasisto! Wiem, że liczby dodatnie i ujemne mogą wydawać się na początku trochę zagmatwane. Widzę, że czasami masz problem z tym, kiedy odejmować, kiedy dodawać, a kiedy w ogóle pojawia się ten minus. Spokojnie, każdy przez to przechodził. Zrozumienie tych liczb jest naprawdę ważne, nie tylko w matematyce, ale i w życiu codziennym. Mam nadzieję, że ten artykuł pomoże Ci zrozumieć te zagadnienia.

Po co nam te liczby ujemne?

Zanim zaczniemy liczyć, zastanówmy się, dlaczego w ogóle potrzebujemy liczb ujemnych. Pomyśl o tym, że świat nie zawsze jest tylko "na plusie".

Temperatura: Czy kiedykolwiek słyszałeś o temperaturze poniżej zera? Na przykład -5 stopni Celsjusza? To jest właśnie liczba ujemna w akcji! Pokazuje, że jest chłodniej niż 0 stopni.
Długi: Jeżeli pożyczasz od kogoś pieniądze, powiedzmy 20 zł, to masz dług. Możemy to zapisać jako -20 zł. To pokazuje, że jesteś "pod kreską".
Położenie: Wyobraź sobie oś liczbową. Zero jest punktem odniesienia. Liczby dodatnie są po prawej stronie, a liczby ujemne po lewej. Możemy użyć ich do określania położenia poniżej poziomu morza (np. -10 metrów) albo w windzie (piętro -1 w garażu).

Widzisz? Liczby ujemne pomagają nam opisywać sytuacje, które są przeciwne do "normalnych" lub "pozytywnych". To bardzo użyteczne narzędzie!

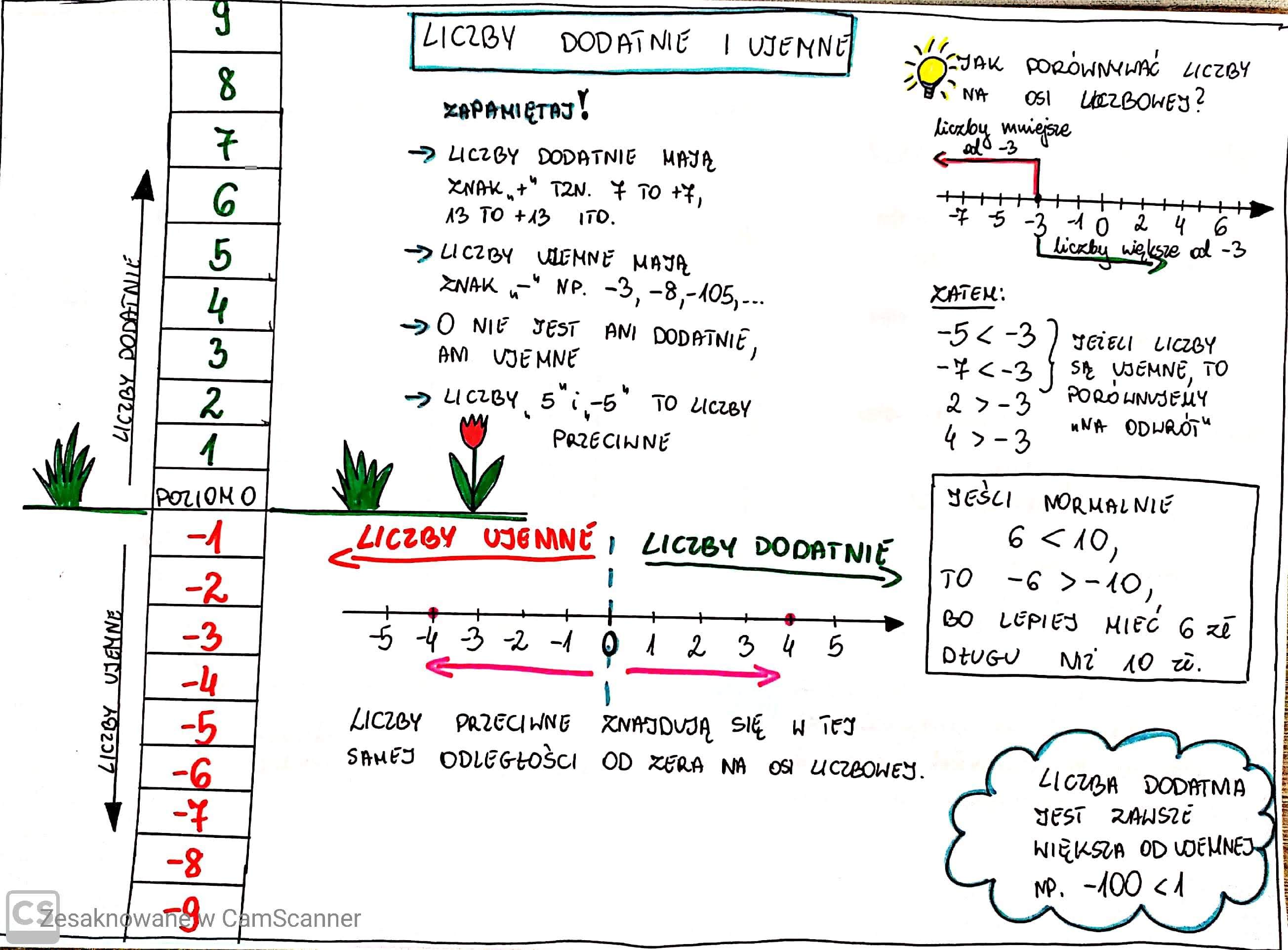
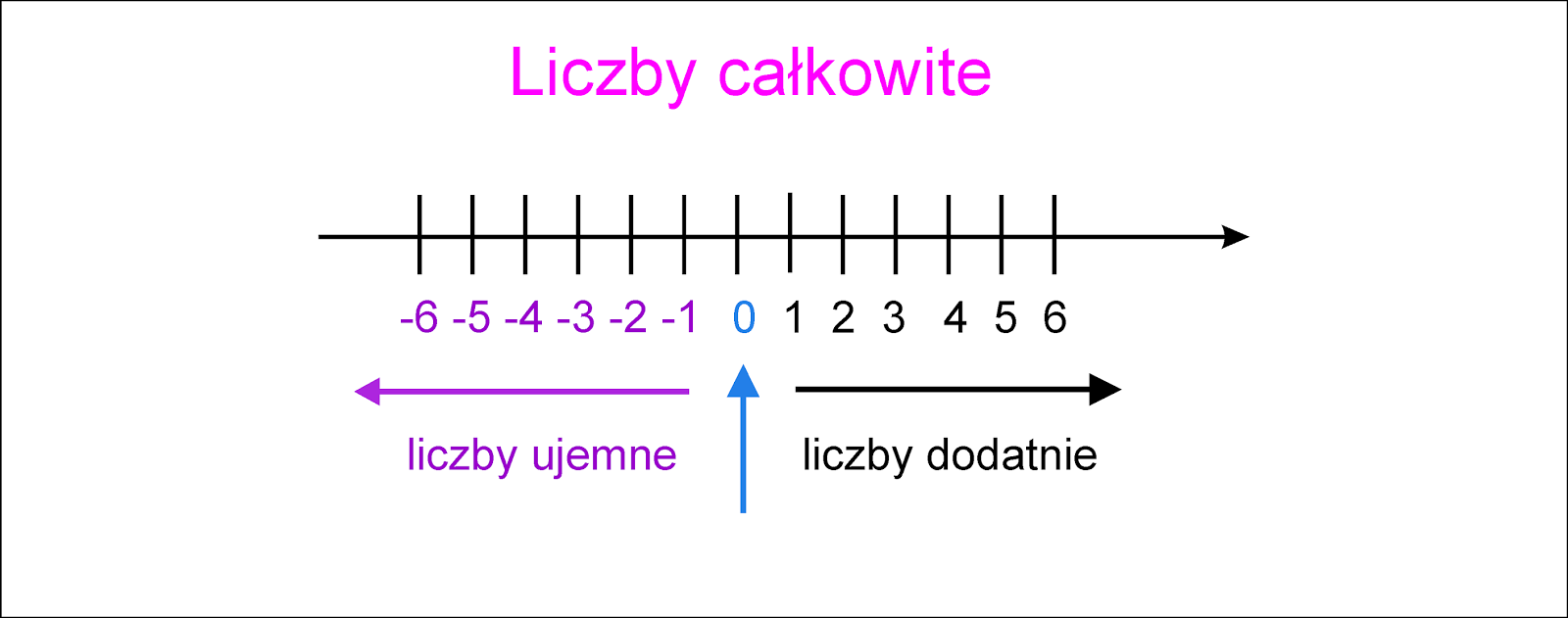
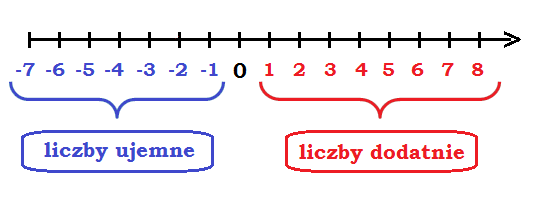
Liczby dodatnie i ujemne na osi liczbowej

Oś liczbowa to nasz przyjaciel! Wyobraź sobie prostą linię, na której pośrodku jest zero. Na prawo od zera mamy liczby dodatnie: 1, 2, 3, 4 i tak dalej, aż do nieskończoności. Na lewo od zera mamy liczby ujemne: -1, -2, -3, -4 i tak dalej, również aż do nieskończoności.

Kilka ważnych rzeczy do zapamiętania:

Im bardziej na prawo jesteś na osi liczbowej, tym większa jest liczba. Na przykład, 5 jest większe niż 2, a 0 jest większe niż -3.
Im bardziej na lewo jesteś na osi liczbowej, tym mniejsza jest liczba. Na przykład, -5 jest mniejsze niż -2, a -10 jest mniejsze niż 0.

Pomyśl o tym jak o termometrze. Im wyższa liczba, tym cieplej. Im niższa liczba, tym zimniej. Dokładnie tak samo działa to na osi liczbowej!

Dodawanie i odejmowanie liczb dodatnich i ujemnych

Tutaj zaczyna się prawdziwa zabawa! Dodawanie i odejmowanie liczb dodatnich i ujemnych może być trochę mylące, ale z kilkoma prostymi zasadami wszystko stanie się jasne.

1. Dodawanie liczb o tych samych znakach:

Jeśli dodajesz dwie liczby dodatnie, to wynik jest zawsze dodatni. Na przykład: 3 + 5 = 8. To proste, prawda?
Jeśli dodajesz dwie liczby ujemne, to wynik jest zawsze ujemny. Dodajesz wartości bezwzględne liczb, a następnie dodajesz znak minus. Na przykład: -3 + (-5) = -8. Pomyśl o tym jak o dodawaniu długów. Jak masz 3 zł długu i dodasz do tego 5 zł długu, to masz w sumie 8 zł długu.

2. Dodawanie liczb o różnych znakach:

Jeśli dodajesz liczbę dodatnią i liczbę ujemną, to musisz odjąć mniejszą wartość bezwzględną od większej. Następnie, wynik ma znak liczby, która miała większą wartość bezwzględną. Na przykład:

-7 + 4 = -3 (7 jest większe niż 4, więc wynik ma znak minus)
5 + (-2) = 3 (5 jest większe niż 2, więc wynik ma znak plus)

3. Odejmowanie liczb dodatnich i ujemnych:

Tutaj jest pewien trik: odejmowanie liczby ujemnej to to samo co dodawanie liczby dodatniej! Zamiast odejmować, możesz zmienić znak liczby, którą odejmujesz, i zamienić odejmowanie na dodawanie.

5 - (-2) = 5 + 2 = 7
-3 - (-4) = -3 + 4 = 1
-2 - 5 = -2 + (-5) = -7

Pamiętaj, że odejmowanie to tak naprawdę dodawanie liczby przeciwnej!

Przykłady z życia wzięte

Żeby lepiej to zrozumieć, popatrzmy na kilka przykładów z życia codziennego:

Temperatura: Dziś rano było -2 stopnie Celsjusza. W ciągu dnia temperatura wzrosła o 5 stopni. Jaka jest temperatura teraz? -2 + 5 = 3 stopnie Celsjusza.
Dług: Kasia miała 10 zł. Pożyczyła od koleżanki 15 zł. Jaki jest stan jej konta? 10 - 15 = -5 zł. Kasia ma 5 zł długu.
Położenie: Helikopter wzniósł się na wysokość 100 metrów, a następnie obniżył o 30 metrów. Na jakiej wysokości znajduje się teraz? 100 - 30 = 70 metrów.

Częste błędy i jak ich unikać

Wiem, że na początku łatwo się pomylić. Oto kilka najczęstszych błędów i wskazówki, jak ich unikać:

Zapominanie o znaku: Zawsze pamiętaj o znaku (+ lub -) przed liczbą! To bardzo ważne!
Mylenie dodawania i odejmowania: Upewnij się, że wiesz, czy masz dodać, czy odjąć liczby. Jeśli masz odejmowanie liczby ujemnej, pamiętaj, żeby zamienić to na dodawanie liczby dodatniej.
Błędne określanie znaku wyniku: Zwróć uwagę na to, która liczba ma większą wartość bezwzględną, gdy dodajesz liczby o różnych znakach. To ona dyktuje znak wyniku.

Żeby uniknąć błędów, ćwicz! Rozwiązuj jak najwięcej zadań. Im więcej będziesz ćwiczył, tym lepiej to zrozumiesz i tym rzadziej będziesz się mylił.

Przeciwstawne punkty widzenia?

Niektórzy mogą argumentować, że liczby ujemne są "sztuczne" albo "niepotrzebne". Mówią, że w realnym świecie nie można mieć "ujemnej" ilości czegoś. Ale pomyśl o tym w ten sposób: liczby ujemne to po prostu sposób na opisywanie sytuacji, które są przeciwne do czegoś. Nie musisz myśleć o nich dosłownie, jako o "ujemnej ilości", ale raczej jako o wskazaniu kierunku (np. w lewo zamiast w prawo, w dół zamiast w górę) lub stanu (np. dług zamiast oszczędności). Takie podejście pozwala nam na upraszczanie wielu obliczeń i modelowanie rzeczywistości w bardziej efektywny sposób.

Podsumowanie i co dalej?

Liczby dodatnie i ujemne to bardzo ważna część matematyki i naszego codziennego życia. Zrozumienie ich zasad pozwala nam na rozwiązywanie wielu problemów i lepiej opisywać świat wokół nas.

Żeby utrwalić swoją wiedzę: