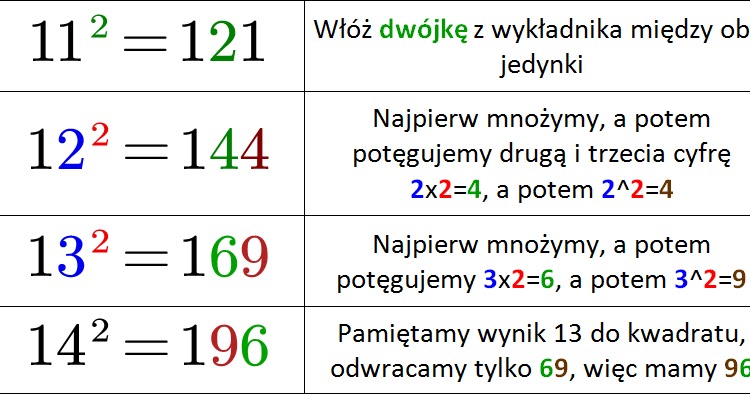
Liczba Pierwiastek 3 Stopnia Z 7 3

W świecie matematyki, pierwiastki odgrywają kluczową rolę, umożliwiając nam rozwiązywanie równań i analizowanie zależności między liczbami. Jednym z przykładów jest pierwiastek trzeciego stopnia, który może być bardziej abstrakcyjny niż pierwiastek kwadratowy, ale równie istotny. W niniejszym artykule szczegółowo przyjrzymy się liczbie, która nas interesuje – pierwiastkowi trzeciego stopnia z 73. Zbadamy jego właściwości, sposoby obliczania, a także jego obecność w realnych zastosowaniach. Celem jest jasne i przystępne przedstawienie tematu, bez zbędnych uproszczeń, aby czytelnik mógł w pełni zrozumieć omawiane zagadnienie.

Czym Jest Pierwiastek Trzeciego Stopnia?

Zanim przejdziemy do konkretnego przykładu, warto ugruntować podstawową definicję. Pierwiastek trzeciego stopnia z danej liczby (oznaczany jako ∛x) to taka liczba, która podniesiona do potęgi trzeciej (do sześcianu) daje liczbę wyjściową. Innymi słowy, jeśli ∛x = y, to y³ = x. Dla przykładu, ∛8 = 2, ponieważ 2³ = 2 * 2 * 2 = 8. Ważne jest, aby pamiętać, że w zbiorze liczb rzeczywistych, każdy pierwiastek trzeciego stopnia z liczby rzeczywistej również jest liczbą rzeczywistą. W odróżnieniu od pierwiastka kwadratowego, pierwiastek trzeciego stopnia może być obliczany zarówno dla liczb dodatnich, jak i ujemnych (np. ∛-8 = -2).

Pierwiastek Trzeciego Stopnia z 73: Wprowadzenie

Naszym celem jest zrozumienie ∛73. Ponieważ 73 nie jest idealnym sześcianem (czyli nie jest wynikiem podniesienia żadnej liczby całkowitej do potęgi trzeciej), jego pierwiastek trzeciego stopnia będzie liczbą niewymierną, czyli liczbą, której nie da się dokładnie wyrazić jako ułamek zwykły. Oznacza to, że jego rozwinięcie dziesiętne będzie nieskończone i nieokresowe. Dlatego będziemy musieli posłużyć się metodami przybliżonymi lub kalkulatorami, aby znaleźć jego wartość.

Metody Obliczania Pierwiastka Trzeciego Stopnia z 73

Istnieje kilka metod, które możemy zastosować, aby obliczyć przybliżoną wartość ∛73. Przyjrzyjmy się kilku z nich:

Metoda Przybliżeń

Jest to podstawowa metoda, która polega na zgadywaniu i sprawdzaniu. Wiemy, że 4³ = 64, a 5³ = 125. Ponieważ 73 leży pomiędzy 64 a 125, wiemy, że ∛73 musi leżeć pomiędzy 4 a 5. Możemy następnie spróbować 4.1, 4.2, 4.3 itd., aby zawęzić przedział. Im więcej prób wykonamy, tym dokładniejsze będzie nasze przybliżenie. Na przykład, 4.1³ ≈ 68.921, a 4.2³ ≈ 74.088. Zatem ∛73 jest bliższe 4.2 niż 4.1. Możemy kontynuować ten proces, obliczając 4.15³, 4.16³ itd., aby uzyskać jeszcze dokładniejsze przybliżenie.

Metoda Newtona-Raphsona

Ta metoda iteracyjna jest bardziej zaawansowana i pozwala na szybsze znalezienie przybliżonej wartości. Opiera się na następującym wzorze:

x_n+1 = x_n - f(x_n)/f'(x_n)

W naszym przypadku, chcemy znaleźć pierwiastek równania x³ - 73 = 0, więc f(x) = x³ - 73, a f'(x) = 3x². Zatem wzór przyjmuje postać:

x_n+1 = x_n - (x_n³ - 73) / (3x_n²)

Zaczynamy od jakiegoś przybliżenia początkowego, np. x₀ = 4. Następnie iteracyjnie obliczamy kolejne przybliżenia:

x₁ = 4 - (4³ - 73) / (3 * 4²) = 4 - (-9) / 48 = 4 + 0.1875 = 4.1875

x₂ = 4.1875 - (4.1875³ - 73) / (3 * 4.1875²) ≈ 4.1875 - (73.56 - 73) / (52.69) ≈ 4.1875 - 0.0106 ≈ 4.1769

Po kilku iteracjach, wartość będzie się stabilizować, dając nam coraz dokładniejsze przybliżenie ∛73.

Użycie Kalkulatora lub Oprogramowania

Najprostszą i najdokładniejszą metodą jest oczywiście użycie kalkulatora naukowego lub oprogramowania matematycznego (np. Wolfram Alpha, MATLAB, Python z biblioteką NumPy). Wprowadzając ∛73, otrzymamy wynik:

∛73 ≈ 4.179339197

Zastosowania Pierwiastka Trzeciego Stopnia w Praktyce

Choć obliczanie pierwiastka trzeciego stopnia może wydawać się abstrakcyjne, ma on wiele praktycznych zastosowań w różnych dziedzinach nauki i inżynierii:

Obliczenia Geometrii

Pierwiastki trzeciego stopnia są wykorzystywane przy obliczaniu wymiarów obiektów trójwymiarowych. Na przykład, jeśli znamy objętość sześcianu, możemy obliczyć długość jego boku, wyciągając pierwiastek trzeciego stopnia z objętości. Podobnie, w bardziej skomplikowanych kształtach, pierwiastki trzeciego stopnia mogą pojawiać się w równaniach opisujących zależności między wymiarami a objętością.

Inżynieria Materiałowa

W inżynierii materiałowej, pierwiastki trzeciego stopnia mogą pojawiać się w modelach opisujących właściwości materiałów, takie jak ich gęstość, moduł Younga czy współczynnik Poissona. W szczególności, przy analizie naprężeń i odkształceń w ciałach stałych, pierwiastki trzeciego stopnia mogą być używane do wyznaczania parametrów geometrycznych, które wpływają na wytrzymałość i stabilność konstrukcji.

Akustyka

W akustyce, pierwiastki trzeciego stopnia mogą być używane w równaniach opisujących propagację fal dźwiękowych. Na przykład, prędkość dźwięku w danym ośrodku zależy od jego gęstości i ściśliwości, a te parametry mogą być związane z pierwiastkami trzeciego stopnia. Ponadto, w projektowaniu pomieszczeń o dobrej akustyce, obliczenia z udziałem pierwiastków trzeciego stopnia mogą pomóc w optymalizacji kształtu i wymiarów, aby zminimalizować echo i rezonanse.

Statystyka

W statystyce, odchylenie standardowe i wariancja są podstawowymi miarami rozproszenia danych. Czasami, do analizy danych o skośnym rozkładzie, używa się transformacji potęgowych, w tym pierwiastków trzeciego stopnia, aby przybliżyć rozkład do normalnego. Pozwala to na bardziej efektywne zastosowanie metod statystycznych, które zakładają normalność rozkładu.

Przykład Realnego Zastosowania: Projektowanie Zbiornika

Wyobraźmy sobie, że projektujemy zbiornik w kształcie sześcianu o określonej pojemności. Załóżmy, że potrzebujemy zbiornika, który pomieści 73 metry sześcienne wody. Aby obliczyć, jak długa musi być krawędź tego sześcianu, musimy obliczyć ∛73. Otrzymujemy wynik w przybliżeniu 4.179 metra. Oznacza to, że każdy bok sześcianu musi mieć długość około 4.179 metra, aby zbiornik miał wymaganą pojemność. Ten prosty przykład ilustruje, jak pierwiastek trzeciego stopnia może być używany w praktycznych obliczeniach inżynierskich.

Podsumowanie i Wnioski

Pierwiastek trzeciego stopnia z 73 to liczba niewymierna, której przybliżona wartość wynosi 4.179339197. Choć samo obliczanie tej wartości może wydawać się abstrakcyjne, pierwiastki trzeciego stopnia mają szerokie zastosowanie w różnych dziedzinach nauki i inżynierii, od obliczeń geometrycznych i inżynierii materiałowej po akustykę i statystykę. Zrozumienie koncepcji pierwiastka trzeciego stopnia i metod jego obliczania jest kluczowe dla wielu profesjonalistów, którzy zajmują się analizą danych, projektowaniem konstrukcji i rozwiązywaniem problemów inżynierskich.

Zachęcamy do dalszego zgłębiania tajników matematyki i odkrywania, jak pozornie abstrakcyjne koncepcje znajdują swoje zastosowanie w otaczającym nas świecie. Eksploracja matematyki może prowadzić do fascynujących odkryć i głębszego zrozumienia praw rządzących naszym wszechświatem. Nie bój się matematyki! Wykorzystaj wiedzę zdobytą w tym artykule, by z większą pewnością rozwiązywać problemy, w których pojawia się pierwiastek trzeciego stopnia.