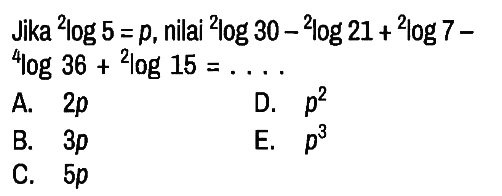Liczba 2log 3 2log 5 2 2 Jest Równa

Hej! Zastanawiasz się, co to za tajemnicze wyrażenie: Liczba 2log 3 2log 5 2 2 Jest Równa? Brzmi skomplikowanie, ale spokojnie! Rozłożymy to na czynniki pierwsze i pokażemy, że wcale nie jest takie straszne. W tym artykule krok po kroku wyjaśnimy, co oznaczają poszczególne elementy i jak rozwiązać to zadanie. Przygotuj się na małą podróż po świecie logarytmów!

Co to właściwie jest logarytm?

Zanim przejdziemy do konkretnego przykładu, musimy zrozumieć, czym jest logarytm. Najprościej mówiąc, logarytm odpowiada na pytanie: do jakiej potęgi muszę podnieść pewną liczbę (zwaną podstawą logarytmu), żeby otrzymać inną liczbę (zwaną liczbą logarytmowaną)?

Formalnie zapisujemy to tak: log_ab = c, co oznacza, że a^c = b.

Przykład z życia: Wyobraź sobie, że masz kolonię bakterii, która podwaja się co godzinę. Na początku masz 1 bakterię. Po ilu godzinach będziesz mieć 8 bakterii? Odpowiedź brzmi 3, ponieważ 2³ = 8. Możemy to zapisać jako log₂8 = 3. Podstawa logarytmu to 2 (bo bakterie się podwajają), liczba logarytmowana to 8 (bo chcemy wiedzieć, kiedy będzie ich 8), a wynik logarytmu to 3 (ilość godzin).

Kluczowe pojęcia:

• Podstawa logarytmu (a): Liczba, którą podnosimy do potęgi. Musi być dodatnia i różna od 1.
• Liczba logarytmowana (b): Liczba, którą chcemy otrzymać. Musi być dodatnia.
• Wynik logarytmu (c): Wykładnik potęgi, do której musimy podnieść podstawę, żeby otrzymać liczbę logarytmowaną.

Rodzaje logarytmów

Istnieją różne rodzaje logarytmów, ale dwa najważniejsze to:

• Logarytm dziesiętny: Ma podstawę 10 i zapisujemy go jako log b (bez zaznaczonej podstawy) lub log₁₀b. Na przykład, log 100 = 2, bo 10² = 100.
• Logarytm naturalny: Ma podstawę e (liczba Eulera, w przybliżeniu 2.71828) i zapisujemy go jako ln b lub log_eb. Jest bardzo ważny w matematyce i fizyce.

Przejdźmy do zadania: Liczba 2log 3 2log 5 2 2 Jest Równa

Teraz, kiedy już rozumiemy, czym są logarytmy, możemy się przyjrzeć temu wyrażeniu. Zauważ, że trochę je przekształcimy, aby było czytelniejsze. Zakładamy, że chodzi o następujące wyrażenie:

2 * log₃(2) * log₅(2) * 2

Czyli mamy mnożenie kilku liczb, w tym logarytmów.

Wykorzystanie własności logarytmów

Aby uprościć to wyrażenie, musimy skorzystać z kilku ważnych własności logarytmów. Jedną z nich jest wzór na zamianę podstawy logarytmu:

log_ab = log_cb / log_ca

Ten wzór pozwala nam zamienić podstawę logarytmu na dowolną inną podstawę c. Wybierzmy jako nową podstawę liczbę 2. Wtedy:

log₃(2) = log₂(2) / log₂(3) = 1 / log₂(3) (bo log₂(2) = 1)

Podobnie:

log₅(2) = log₂(2) / log₂(5) = 1 / log₂(5)

Teraz możemy wstawić te wartości do naszego wyrażenia:

2 * log₃(2) * log₅(2) * 2 = 2 * (1 / log₂(3)) * (1 / log₂(5)) * 2 = 4 / (log₂(3) * log₂(5))

Czyli mamy:

4 / (log₂(3) * log₂(5))

Przekształcenie i obliczenie

Teraz to wyrażenie można zostawić w takiej formie, albo można skorzystać z kalkulatora, aby obliczyć przybliżoną wartość. Żeby to zrobić, potrzebujesz kalkulatora, który oblicza logarytmy o podstawie 2. Jeśli Twój kalkulator liczy tylko logarytmy o podstawie 10 (czyli log) lub o podstawie e (czyli ln), to musisz użyć wzoru na zamianę podstawy jeszcze raz, aby przeliczyć na te podstawy.

Na przykład:

log₂(3) = log(3) / log(2) ≈ 1.585

log₂(5) = log(5) / log(2) ≈ 2.322

Wtedy:

4 / (log₂(3) * log₂(5)) ≈ 4 / (1.585 * 2.322) ≈ 4 / 3.675 ≈ 1.089

Więc liczba 2 * log₃(2) * log₅(2) * 2 jest w przybliżeniu równa 1.089.

Podsumowanie

Uff, to była długa droga! Przeanalizowaliśmy, czym jest logarytm, jakie są jego rodzaje, poznaliśmy wzór na zamianę podstawy logarytmu i wykorzystaliśmy go do uproszczenia naszego wyrażenia. Ostatecznie, korzystając z kalkulatora, mogliśmy obliczyć przybliżoną wartość tego wyrażenia.

Pamiętaj, że kluczem do zrozumienia matematyki jest rozkładanie problemów na mniejsze, łatwiejsze do ogarnięcia części. Nie bój się pytać i eksperymentować! Powodzenia w dalszej nauce matematyki! Gratulacje, jeśli dotarłeś aż tutaj! Znasz teraz podstawy logarytmów i potrafisz rozwiązywać bardziej skomplikowane zadania!

Pamiętaj: matematyka to nie tylko wzory, ale przede wszystkim logiczne myślenie i umiejętność rozwiązywania problemów. Baw się nią i odkrywaj jej piękno!