łączy Dwa Wierzchołki Wielokąta Które Nie Należą Do Jednego Boku

W geometrii, figury płaskie odgrywają kluczową rolę w zrozumieniu przestrzeni i relacji między obiektami. Wśród nich, wielokąty wyróżniają się swoją prostotą i wszechstronnością. Złożone z odcinków, które tworzą boki, wielokąty zamykają obszar, definiując jego kształt. Ale co się dzieje, gdy połączymy wierzchołki wielokąta w sposób, który wykracza poza definicję boku? Powstają wtedy specjalne linie, które niosą ze sobą cenne informacje o samej figurze.

Zacznijmy od definicji. Wielokąt to figura geometryczna, ograniczona zamkniętą łamaną zwyczajną. Oznacza to, że składa się z odcinków (boków), które łączą się w punktach (wierzchołkach), tworząc zamkniętą pętlę. Najprostszy wielokąt to trójkąt, posiadający trzy boki i trzy wierzchołki. Dalej mamy czworokąty, pięciokąty, sześciokąty i tak dalej. Nazwa wielokąta pochodzi od liczby jego boków, przy czym liczba boków zawsze równa się liczbie wierzchołków.

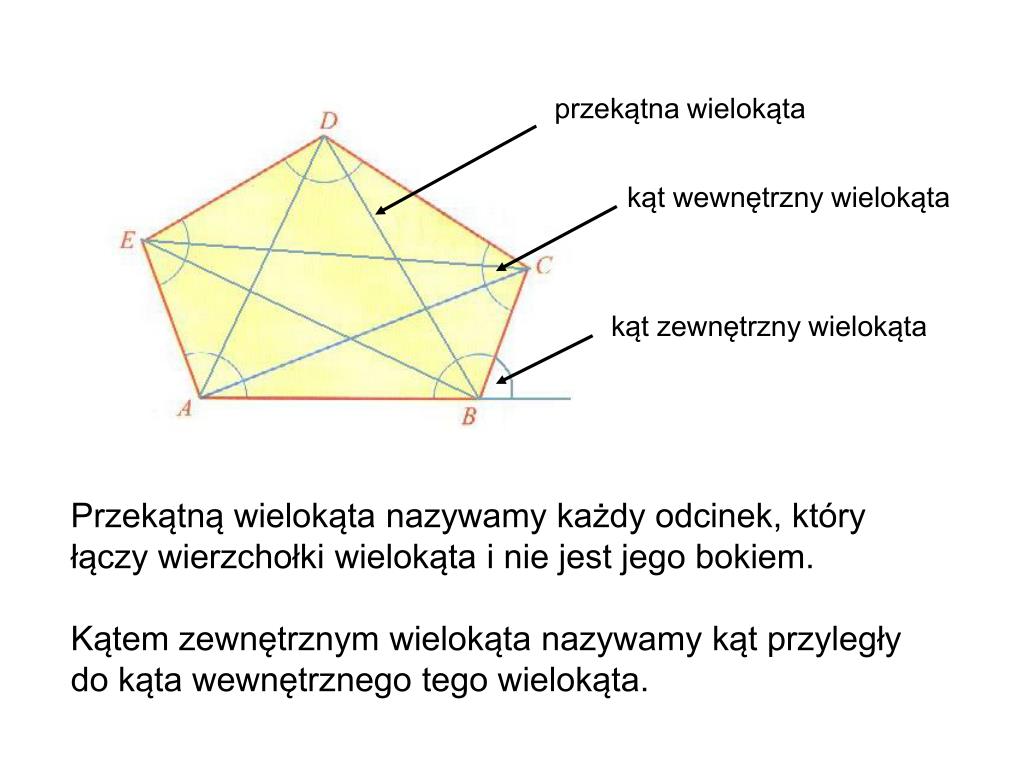
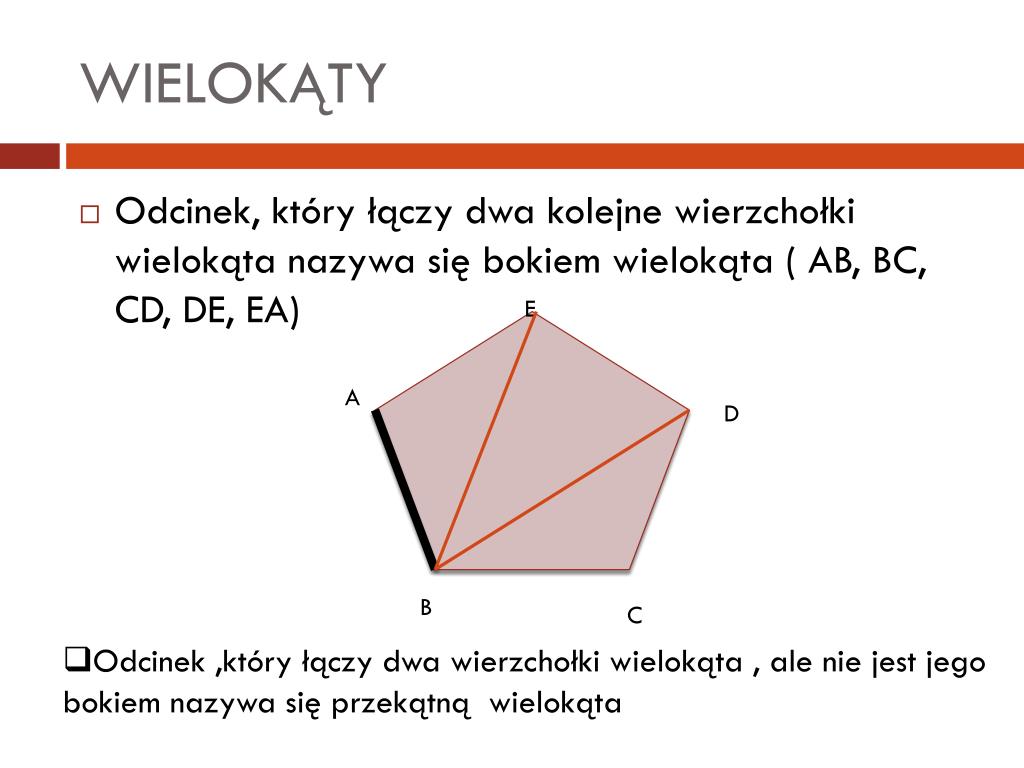
Teraz wyobraźmy sobie dowolny wielokąt, na przykład pięciokąt. Ma on pięć wierzchołków. Możemy oczywiście połączyć sąsiednie wierzchołki, tworząc boki pięciokąta. Ale co się stanie, jeśli połączymy wierzchołek A z wierzchołkiem C, który nie jest z nim bezpośrednio połączony bokiem? Powstanie odcinek, który przecina wnętrze pięciokąta. Taki odcinek nazywamy właśnie odcinkiem łączącym dwa wierzchołki wielokąta, które nie należą do jednego boku.

Aby lepiej to zrozumieć, rozważmy sześciokąt ABCDEF. Boki sześciokąta to AB, BC, CD, DE, EF i FA. Jeśli połączymy wierzchołek A z wierzchołkiem C, otrzymamy odcinek AC. Podobnie, połączenie wierzchołka B z wierzchołkiem D daje odcinek BD. Zauważmy, że ani AC, ani BD nie są bokami sześciokąta. Są to właśnie odcinki łączące dwa wierzchołki wielokąta, które nie należą do jednego boku.

Te odcinki, choć na pierwszy rzut oka wydają się być jedynie dodatkowymi liniami wewnątrz wielokąta, mają fundamentalne znaczenie. Mogą one bowiem dzielić wielokąt na mniejsze figury, takie jak trójkąty i czworokąty. Ta właściwość jest szczególnie przydatna przy obliczaniu pola powierzchni skomplikowanych wielokątów. Zamiast próbować bezpośrednio obliczyć pole wielokąta o nieregularnym kształcie, możemy podzielić go na mniejsze, bardziej regularne figury, obliczyć pole każdej z nich oddzielnie, a następnie zsumować wyniki.

Właściwości i Zastosowania

Odcinki łączące dwa wierzchołki wielokąta, które nie należą do jednego boku, mają kilka interesujących właściwości. Przede wszystkim, liczba takich odcinków rośnie wraz ze wzrostem liczby boków wielokąta. W trójkącie nie ma żadnych takich odcinków, ponieważ każdy wierzchołek jest połączony z dwoma pozostałymi bokami. W czworokącie mamy już dwa takie odcinki, w pięciokącie pięć, a w sześciokącie dziewięć.

Istnieje wzór na obliczenie liczby odcinków łączących dwa wierzchołki wielokąta, które nie należą do jednego boku. Jeśli n oznacza liczbę wierzchołków (a zatem i boków) wielokąta, to liczba tych odcinków wynosi n(n-3)/2. Sprawdźmy to dla kilku przykładów:

• Dla czworokąta (n=4): 4(4-3)/2 = 4(1)/2 = 2
• Dla pięciokąta (n=5): 5(5-3)/2 = 5(2)/2 = 5
• Dla sześciokąta (n=6): 6(6-3)/2 = 6(3)/2 = 9

Wzór potwierdza nasze obserwacje.

Zastosowania tych odcinków są różnorodne. Jak już wspomniano, pozwalają one na dekompozycję wielokąta na mniejsze, prostsze figury, co ułatwia obliczanie pola powierzchni. Ponadto, odcinki te mogą być wykorzystywane do analizy symetrii wielokąta. Na przykład, w wielokącie foremnym odcinki łączące wierzchołki oddalone od siebie o taką samą liczbę boków będą miały równe długości.

W architekturze i inżynierii, znajomość właściwości tych odcinków może być przydatna przy projektowaniu konstrukcji o specyficznych właściwościach. Na przykład, odpowiednie rozmieszczenie tych odcinków w konstrukcji kratownicowej może zwiększyć jej wytrzymałość i stabilność.

Przykłady i Ilustracje

Aby jeszcze lepiej zilustrować omawiane zagadnienie, rozważmy kilka konkretnych przykładów.

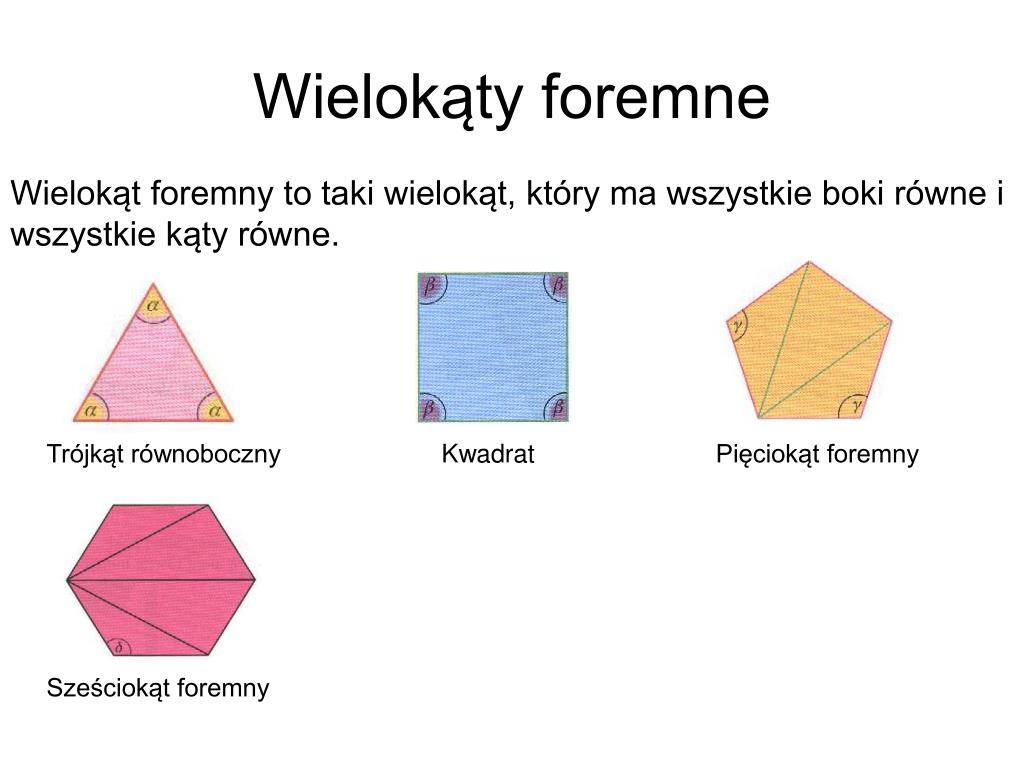
Kwadrat: Kwadrat ABCD ma cztery boki (AB, BC, CD, DA) i cztery wierzchołki (A, B, C, D). Odcinki łączące wierzchołki, które nie należą do jednego boku, to AC i BD. Są to oczywiście przekątne kwadratu. Przekątne kwadratu przecinają się pod kątem prostym i dzielą się na połowy, co jest cechą charakterystyczną kwadratu.

Pięciokąt foremny: Pięciokąt foremny ABCDE ma pięć boków i pięć wierzchołków. Odcinki łączące wierzchołki, które nie należą do jednego boku, to AC, AD, BD, BE i CE. Te odcinki tworzą wewnątrz pięciokąta foremną gwiazdę, znaną jako pentagram. Pentagram ma wiele interesujących właściwości matematycznych i symbolicznych.

Sześciokąt foremny: Sześciokąt foremny ABCDEF ma sześć boków i sześć wierzchołków. Odcinki łączące wierzchołki, które nie należą do jednego boku, to AC, AD, AE, BD, BE, BF, CE, CF i DF. Można zauważyć, że niektóre z tych odcinków są dłuższe od innych. Na przykład, odcinek AD jest dłuższy od odcinka AC. Odcinki AD, BE i CF przechodzą przez środek sześciokąta i dzielą go na sześć trójkątów równobocznych.

Podsumowanie

Odcinki łączące dwa wierzchołki wielokąta, które nie należą do jednego boku, są ważnym elementem geometrii. Umożliwiają one dekompozycję wielokątów na mniejsze figury, co ułatwia obliczanie pola powierzchni i analizę symetrii. Liczba tych odcinków rośnie wraz ze wzrostem liczby boków wielokąta, zgodnie z wzorem n(n-3)/2. Znajomość właściwości tych odcinków może być przydatna w różnych dziedzinach, takich jak architektura, inżynieria i grafika komputerowa. Poprzez analizę tych odcinków, możemy lepiej zrozumieć geometrię wielokątów i ich zastosowania w praktyce. Rozważając te "ukryte" linie, możemy odkryć nowe perspektywy i zrozumieć fundamentalne zasady, które rządzą światem kształtów. A to prowadzi do głębszego zrozumienia samej geometrii i jej wpływu na otaczający nas świat.